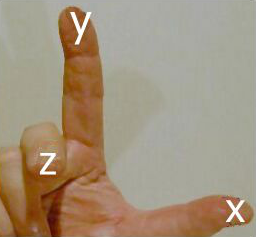1.3.5 Vektoren

Man stelle sich nun einen mit der Geschwindigkeit v rollenden Wagen vor (siehe Abb.1), der wie ein Rollbrett nach allen Seiten frei beweglich ist. In den auf diesem Wagen liegenden Schwamm schlage ein Luftgewehrgeschoss mit der Geschwindigkeit u ein. Der Einschlag des Geschosses ändert in diesem Fall auch die Bewegungsrichtung des Wagens. Damit die Anwendung der an eindimensionalen Bewegungen gewonnenen

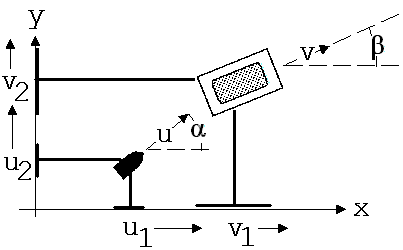
Abb.1: Draufsicht

Gesetze möglich ist, werden das Geschoss und der Experimentierwagen auf die beiden Achsen des Koordinatensystems orthogonal projiziert. Die Projektionen bewegen sich vor dem Einschlag der Kugel in x-Richtung mit u1 und v1 und in y-Richtung mit u2 und v2. Nach dem Einschlag der Kugel bewegt sich der Wagen zusammen mit der darin steckenden Kugel mit der Geschwindigkeit w1 in x- und w2 in y-Richtung. Der Impulssatz gilt für beide Bewegungsrichtungen!

mG · u1 + mW · v1 = (mG + mW) · w1; mG · u2 + mG · v2 = (mG + mW) · w2

Aufgabe:

Gegeben sei mG = 0,5 g, α = 30°, u = 60 m/s und mW = 200g, β = 20°, v = 0,5 m/s

Welche Geschwindigkeit und welche Bewegungsrichtung hat der Wagen nach dem Stoß durch die Kugel ?

Zur Anwendung des Impulssatzes müssen anhand der Angaben die Geschwindigkeiten beider Körper in x und y-Richtung berechnet werden. Zu diesem Zweck werden die Geschwindigkeiten vor dem Stoß durch Pfeile veranschaulicht. Die Pfeile werden so angelegt, dass sie nicht nur die Bewegungsrichtungen der Gegenstände, sondern auch noch mit ihren Längen deren Geschwindigkeiten anzeigen (siehe Abb. 2).

Die Länge L eines Pfeils kann z.B. gleich dem Weg sein, den ein Körper in 1 s, in 0,1 s oder in 0,01 s zurücklegt. Je nach gewählter Zeit repräsentiert ein solcher Pfeil die Geschwindigkeiten v = L/1 s bzw. v= L/0,1 s bzw. v=L/0,01 s. Man sollte sich den Pfeil wie einen Zahlenstrahl skaliert vorstellen, so dass man an der Spitze den zugeordneten Wert ablesen kann. Derartige Pfeile setzt man immer dann ein, wenn neben der Angabe eines Maßes noch eine Richtungsbeschreibung nötig ist, man nennt sie Vektoren.

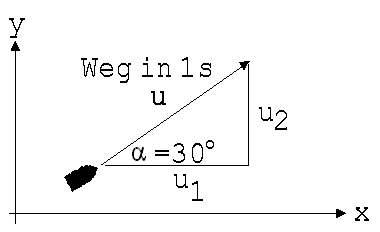
Abb. 2

u1 und u2 erhält man wie folgt: u1 = u · cos α; u2 = u · sin α.

Auf gleiche Weise erhält man für den Wagen: v1 = v · cos β; v2 = v · sin β.

Für die Geschwindigkeiten des Wagens nach dem Stoß in x- und y-Richtung gilt:

(mW + mG ) · w1 = mG · u · cos α + mW · v · cos β

(mW + mG ) · w2 = mG · u · sin α + mW · v · sin β

w1 = ( mG · u · cos α + mW · v · cos β ) / (mW + mG ) = 0,598 m/s

w2 = (mG · u · sin α + mW · v · sin β) / (mW + mG ) = 0,245 m/s

Wiederholung zum Thema „Winkelfunktionen“

Mit den Ergebnissen für w1 und w2 ist die Aufgabe fast gelöst. Es fehlen nur noch Angaben über die Bewegungsrichtung und die Gesamtgeschwindigkeit w des Wagens nach dem Stoß.

Zu diesem Zweck wird der zu w1 und w2 passende Geschwindigkeitsvektor dargestellt Die Gesamtgeschwindigkeit w erhält man mit Hilfe des Satzes von Pythagoras (Herleitung dieses Satzes).. w1 und w2 beschreiben die Wege, die nach dem Einschlag der Kugel vom Wagen in einer Sekunde in x und y-Richtung zurückgelegt werden. Der Pfeil zeigt die Gesamtgeschwindigkeit nach Größe und Richtung an.

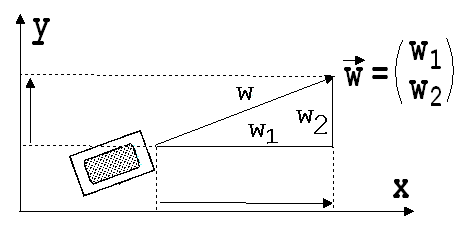
Abb. 3

w2 = w12 + w22 → 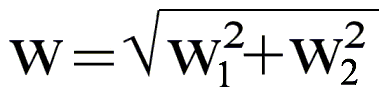= 0,646 m/s (Betrag des Vektors w )

Die orthogonalen Projektionen des Vektors auf die Koordinatenachsen werden Vektorkomponenten genannt (siehe Abb.3). Die zugehörigen Werte wie w1 und w2 heißen Vektorkoordinaten.

Ist eine Komponente der Koordinatenachse entgegen gerichtet, dann ist die zugehörende Vektorkoordinate negativ. Die Beschreibung eines Vektors geschieht meistens mit der Angabe seiner Koordinaten, die man normalerweise zu einer mit Klammern eingefassten Säule (oben die x-Koordinate, dann die y-Koordinate und schließlich bei räumlichen Vorgängen noch die z-Koordinate), manchmal aber auch aus drucktechnischen Gründen in einer Reihe anordnet, z.B. so:{w1 ; w2; w3}.

Aus dieser Beschreibungsform geht hervor, dass man Vektoren dann als einander gleich ansieht, wenn sie in diesen Koordinaten übereinstimmen. Dies bedeutet Übereinstimmung in Richtung und Länge, nicht jedoch im Anfangspunkt.

Als Zeichen für Vektoren sind Buchstaben mit einem kleinen aufgesetzten Pfeil oder fett gedruckte Buchstaben üblich. Wird ein solcher Buchstabe in Betragszeichen gesetzt, dann meint man den sogenannten Vektorbetrag. Dieser entspricht seiner Länge.

Beispiel: |w| = .

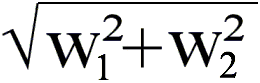Vektorsumme und Vektordifferenz

Zu dem in der Abb. 1 skizzierten Experiment werden die Geschwindigkeiten u, v und w angegeben. Ihnen werden Geschwindigkeitsvektoren u ={u1; u2}; v={v1; v2}; w ={w1; w2} und Impulsvektoren {mG·u1; mG·u2}; { mW ·v1; mW ·v2}; {(mG+mW)·w1; (mG+mW)·w2} zugeordnet. {(mG + mW) ·w1; (mG + mW) ·w2} = { mG·u1 + mW·v1; mG·u2 + mW·v2} wird Summe der Vektoren {mG·u1; mG·u2} und { mW ·v1; mW ·v2} genannt.

Die Vektorsumme zweier Vektoren a und b erhält man demnach, indem man die entsprechenden Koordinaten von a ={a1; a2; a3} und b ={b1; b2; b3}addiert.

a + b = {a1 + b1 ; a2 + b2 ; a3 + b3}

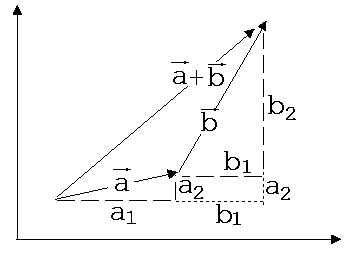
Abb.4

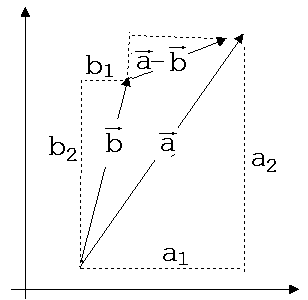
Abb. 5


Der Summenvektor zeigt vom Fuß des Vektors a zur Spitze des Vektors b, wenn der Fuß von b die Spitze von a berührt (siehe Abb.4). a - b = {a1 - b1 ; a2 - b2 ; a3 - b3} heißt Vektordifferenz. Wenn a und b gleiche Fußpunkte haben, dann stellt ein Pfeil von der Spitze von b zur Spitze von a die Vektordifferenz dar (siehe Abb.5).

Das Produkt und der Quotient eines Vektors mit einer Zahl

Anstelle von {mG · u1; mG · u2} und { mW · v1; mW · v2} schreiben wir mG · {u1; u2} und mW · {v1; v2}. Hieran ist erkennbar, wie das Produkt aus einem Vektor a und einer Zahl z definiert ist.

z · a = z·{a1 ; a2 ; a3} = {z · a1 ; z · a2 ; z · a3}

Man nennt die hier beschriebene Multiplikation eines Vektors mit einer Zahl skalare Multiplikation. Sie bewirkt eine Streckung des Vektors a um z (siehe Abb. 6 mit z =3).

Bei Anwendung des Impulssatzes auf den Zusammenstoß zweier Körper mit den Massen m1 und m2 im Raum mussten bisher drei Gleichungen geschrieben werden:

m1· v1 + m2 · u1 = m1 · v1’ + m2 · u1’

m1· v2 + m2 · u2 = m1 · v2’ + m2 · u2’

m1· v3 + m2 · u3 = m1 · v3’ + m2 · u3’

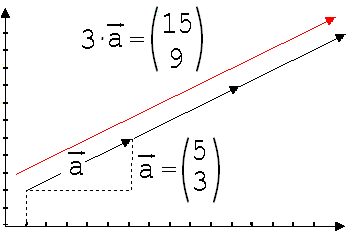
Abb.6

m1 · v1, m2 · u1, m1 · v1’ und m2 · u1’ sind Impulskoordinaten vor und nach dem Stoß. Für diese drei Gleichungen kann nun die kurze Formulierung gegeben werden:

m1 · v + m2 · u = m1 · v’ + m2 · u’

v ={v1; v2; v3 }, u ={u1; u2 ; u3}, v' ={v'1; v'2; v'3 }, u' ={u'1; u'2 ; u'3}

Von nun an soll das Wort Impuls für einen Impulsvektor m · v stehen.

Nach der Definition des hier beschriebenen Produkts ist man geneigt, nach einem entsprechenden Quotienten zu fragen. Ein Quotient a /m (Vektor a durch eine Zahl m) soll so beschaffen sein, dass folgendes gilt: (a/m) · m = a. (1/m) · a hat die Eigenschaft eines solchen Quotienten.

Teilt man einen Vektor a durch seinen Betrag |a|, dann erhält man einen Einheitsvektor, einen Vektor mit dem Betrag 1.

Beispiel: a = {4; 3 }; |a| = 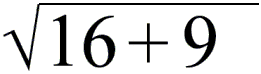= 5 → a / |a| = { 4/5; 3/ 5}

Das Skalarprodukt

Bei dem in der Abb.1 skizzierten Experiment hat der Wagen vor dem Einschlag der Kugel die Geschwindigkeit v und nach dem Einschlag die Geschwindigkeit w. Der Winkel γ, den die Vektoren w und v einschließen, beschreibt die Richtungsänderung des Wagens infolge des Einschlags.

Wie groß ist γ ?

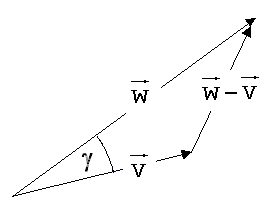
Abb.7

Nach dem Kosinussatz gilt: |w-v|2 = |w|2 + |v|2 – 2·|w| · |v| · cos(γ)

Herleitung des Kosinussatzes

(w1 - v1)2 + (w2 - v2)2 + (w3 - v3)2 = w12 + w22 + w32 + v12 + v22 + v32 - 2·|w| · |v| · cos(γ)

↓

{w12 + w22 + w32 + v12 + v22 + v32 } - 2 · w1 · v1 – 2 ·w2 · v2 - 2·w3 · v3 =

={w12 + w22 + w32 + v12 + v22 + v32 } -2·|w|·|v|·cos(γ)

↓

w1·v1 + w2·v2 + w3·v3 = |w|·|v|·cos(γ) → cos(γ) = (w1·v1 + w2·v2 + w3·v3) / (|w|·|v|)

w1 · v1 + w2 · v2 + w3 · v3 heißt Skalarprodukt w · v der Vektoren w und v.

Unter dem Skalarprodukt zweier beliebiger Vektoren a und b versteht man die Summe aus den Produkten entsprechender Koordinaten.

a · b = a1 ·b1 + a2 ·b2 + a3 ·b3

Das Skalarprodukt gleicht dem Produkt der Vektorbeträge und dem Kosinus des eingeschlossenen Winkels (w1 · v1 + w2 · v2 + w3 · v3 ) = |w| · |v| · cos(γ) .

Anmerkung zum räumlichen Koordinatensystem (Rechtssystem)

Die Koordinaten eines Punktes oder eines Vektors sind normalerweise einem Rechtssystem zuzuordnen.

Dessen Eigenschaften sind: Die x, y und z-Achse verhalten sich ihrer Richtung nach wie der Daumen, der Zeige- und der Mittelfinger der rechten Hand, wenn der Mittelfinger von den beiden anderen rechtwinklig abgespreizt ist (siehe Abb.8).

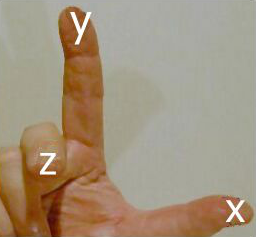
Abb.8