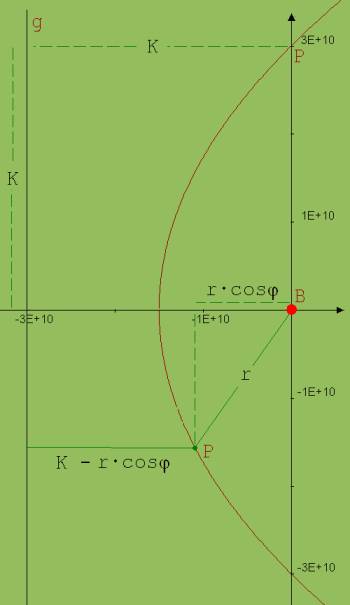
Abb. 1

Die Parabel ist durch folgende Eigenschaft definiert:

Zu einer Parabel gibt es einen Punkte B (Brennpunkt) und eine Gerade g, deren Abstände zu einem willkürlich gewählten Parabelpunkt P übereinstimmen.

K- r · cosφ = r

r = K / (1 + cosφ)

r = K / (1 + ε · cosφ); ε = 1

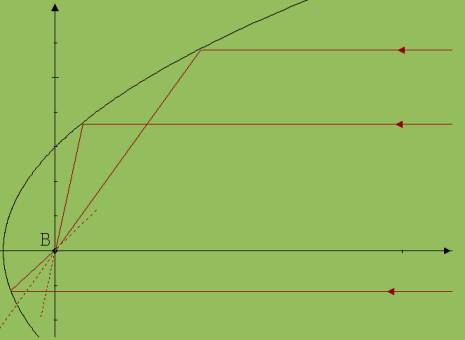
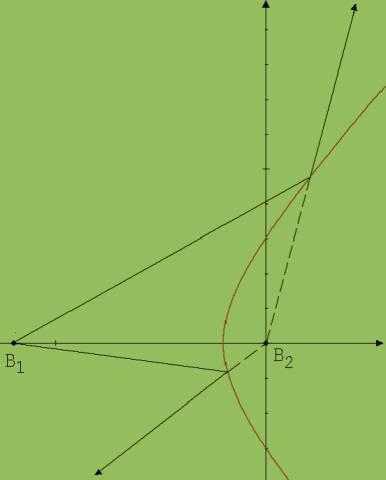
Abb. 2

„Brennpunkt“ als Bezeichnung des Punktes B ist auch hier gerechtfertigt.

Ein spiegelndes Band auf einer Parabel reflektiert einen parallel zur Symmetrieachse einfallenden Lichtstrahl zum  Brennpunkt B hin ( siehe Abb. 2).

Abb. 3

Die Hyperbel ist durch folgende Eigenschaft definiert:

Die Punkte der Hyperbel haben zu zwei gegebenen Punkten B₁ und B₂  Abstände, welche eine konstante Differenz  bilden (siehe Abb. 3 ).

Mit e benennen wir den halben Abstand zwischen den Punkte B₁ und B₂ und mit a die Hälfte der genannten konstanten Differenz (siehe Abb.4). 

Die Hyperbel besteht aus zwei Teilen.

Abb. 4

(2·a + r)² = r² + 4·e² – 4·e·r · cos φ

4 · a² + r² + 4 · a · r = r² + 4·e² - 4·e·r · cos φ

e² - a² = a · r + e·r · cos φ  →   r = (e² - a² ) /( a + e · cos φ)

(e² - a² )/ a = K;  e/a = ε 

e > a   →   |ε| > 1

→  r = K /( 1 + ε · cos φ)

Abb. 5

Die Beiden Punkte B₁ und B₂  heißen Brennpunkte der Hyperbel.

Der Name Brennpunkt für B₁ und B₂ passt hier wieder aus folgendem Grund:

Ein spiegelndes Band auf einer Hyperbel reflektiert von einem Brennpunkt ausgehendes Licht so, dass man den Eindruck hat, die reflektierten Lichtstrahlen kämen vom anderen Brennpunkt. Es entsteht ein virtuelles Bild des einen Brennpunkts am Ort des anderen Brennpunkts (siehe Abb. 5).