Gleichung für die x- und y-Koordinaten einer Hyperbel

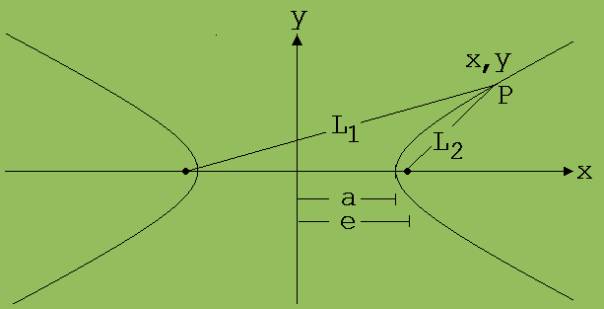
Abb. 1

Der Ellipse wird ein Koordinatensystem zugeordnet. Die x –Achse läuft durch die beiden Brennpunkte, die y-Achse halbiert die Verbindungsstrecke der Brennpunkte rechtwinklig.

L₁ = [(x + e)² + y² ] ^½    ; L₂ = [(x - e)² + y² ] ^½      →      [(x + e)² + y² ] ^½    - [(x - e)² + y² ] ^½     = L₁ – L₂

Legt man P auf die x-Achse, dann ist sofort erkennbar: L₁ – L₂ = 2 · a

[(x + e)² + y² ] ^½    = 2·a + [(x - e)² + y² ] ^½  →  (x + e)² + y²  =  4·a² + (x - e)² + y² + 4· a · [(x - e)² + y² ] ^½ 

↓

e·x -  a² = a · [(x - e)² + y² ] ^½   →     e² · x² + a⁴ - 2·e·x·a² = a² · [(x - e)² + y² ]

(e² – a²) · x² – a² · y² =  a² · (e² – a² )

Für e² - a²  schreiben wir  b²

↓

b² · x² – a² · y² = a² · b²  →    x² / a²  -  y² / b² = 1 (Hyperbelgleichung)