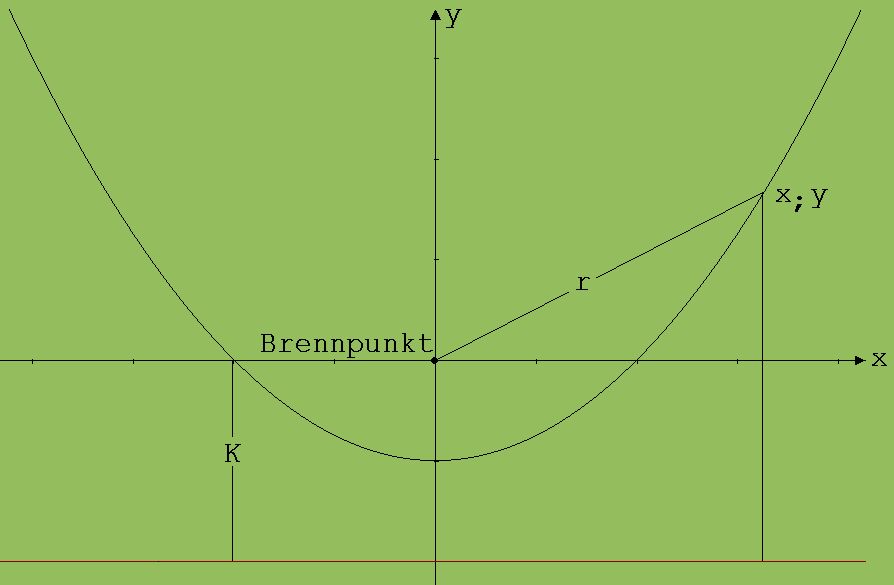
Gleichung für die x- und y-Koordinaten einer Parabel

Abb. 1

r² = x² + y²

(x² + y² )^½ = K + y   ®   (x² + y² ) = K² + y² + 2× K× y    ®   x² = K² +  2× K× y  ®  y =  x² /(2×K) – K / 2 

K/2 ist der Abstand des Brennpunkts vom Parabelscheitel.

Liegt eine Gleichung der Form y = a × x² + b vor, dann beschreibt diese Gleichung eine Parabel. Den Abstand d = K/2 des Brennpunkts vom Scheitel erhält man nach a = 1/(2×K).

a = 1/ (4×d)    ®   d = 1/ (4×a)

Eine Änderung des konstanten Gliedes b bewirkt nur eine Verschiebung parallel zur y-Achse und keine Änderung der Parabelform.