1.9.1 Die Harmonische Schwingung
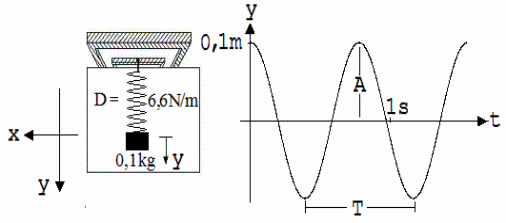
An der Vorderseite der Wippe hängen wir eine Schraubenfeder mit einem Körper G der Masse m = 0,1 kg auf . Nachdem sich die Feder beruhigt hat, wird G nach unten gezogen (y > 0) und anschließend freigegeben. G schwingt auf und nieder und der an die Experimentierwippe angeschlossene Rechner zeichnet das in der Abb.1 sichtbare Diagramm. Mit der Wippe wird D·y gemessen, dies ist die Änderung der auf die Wippe wirkenden Federkraft F bei einer Abweichung y aus der Ruhelage. Aus dem Kraft-Zeit-Diagramm wird ein Weg-Zeit-Diagramm, wenn man zu den Einteilungen der y-Achse nicht Kräfte, sondern stattdessen die ihnen entsprechenden Federdehnungen schreibt.
Siehe https://www.youtube.com/watch?v=wlnEcwHaJmM

Abb. 1
G wird unter der Kraft Fy = - D·y beschleunigt. Das -Zeichen zeigt an, dass die Kraft der Auslenkung entgegen gerichtet ist. Bei genauer Prüfung des Sachverhalts wird man schreiben:
Fy = -D·|s| + m·g - D·y.
s ist die Dehnung der Feder bei ruhendem G.
Beachte: Der Auslenkung nach unten sowie einer nach unten wirkenden Kraft wird ein positiver y- bzw. Fy - Wert zugeordnet.
Fy = - D·y gilt, weil die Gewichtskraft m·g durch die nach oben gerichtete Kraft D·|s| der ruhenden Feder ausgeglichen wird.
Fy = -D·y → -D·y = m·ay → ay = - (D/m)·y
Elongation, Amplitude, Schwingungszeit und Frequenz sind Begriffe, die bei der Behandlung von Schwingungen zu hören sind.
1. Elongation y: Sie ist die augenblickliche Abweichung von der Ruhelage.
2. Amplitude A: Sie ist der Betrag der maximalen Elongation.
3. Schwingungszeit T: Dies ist die Zeit, die während einer Schwingung vergeht.
4. Frequenz f: f = n/t, n ist die Zahl der Schwingungen in der Zeit t. Aus t = n·T folgt: f = n/(n·T) = 1/ T. Die Frequenz gibt die Anzahl der Schwingungen pro Zeiteinheit an, sie gleicht dem Kehrwert der Schwingungsdauer. Für die zugehörende Einheit 1/s schreibt man auch Hz. Dies ist eine Abkürzung vom Nachnamen des Physikers Heinrich Hertz.
Lässt man eine Kugel K in einer auf der Wippe stehenden Schale rotieren, dann wird vom Rechner ein Diagramm gezeichnet, welches man auch einer Federschwingung zuordnen könnte (siehe Abb. 2). Die Projektion P der Kugel auf die Längsseite der Wippe bewegt sich so wie ein an einer Schraubenfeder hin und her schwingender Körper. Vermutlich gilt auch für die Projektion P die Proportionalität ay~y. ay ist in diesem Fall die y-Komponente der Kreisbeschleunigung. Diese hat den Betrag ω2 ·r .
Die hier geäußerte Vermutung ist leicht anhand der Abb.3 beweisbar.
-ay / (ω2 ·r) = y/r → ay = - ω2·y
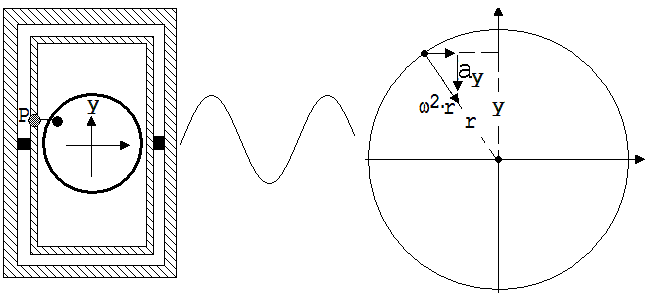
Abb. 2 Abb. 3
Aus ay = - (D/m)·y und ay = - ω2·y folgt:
P sei die Projektion eines gleichmäßig mit ω kreisenden Körpers K auf den Kreisdurchmesser und G ein Körper der Masse m, der an einer Schraubenfeder mit der Federkonstanten D schwingt.
P und G haben bei gleicher Amplitude zu jedem Zeitpunkt den gleichen Abstand vom Schwingungsmittelpunkt, wenn ω2 = D/m ist und wenn P und G gleichzeitig ihre maximale positive Elongation y =A erreichen. Im Fall ω2 = D/m erfahren P und G bei gleicher Elongation gleiche Beschleunigungen. Die Amplitude von P ist gleich dem Radius r der Kreisbahn.
In der Schwingungszeit T dreht sich K um den Winkel 2·π.
2·π/T = ω = √(D/m) → T = 2·π ·√(m/D) → f = [1/(2·π)]·√(D/m)
Eine Schwingung mit rotierendem Zeiger wird nach Anklicken dieser Zeile vorgeführt.
Wird im Programm „Mathe.-Physik“ „Simulation_Rotierender Zeiger zur Überprüfung einer Schwingung_ senkrechte Schwingung“ aufgerufen, dann ist ein rotierender Zeiger zu sehen, dessen Spitze eine waagrechte Strecke mit sich führt (siehe Abb. 4).
Das Federpendel wird so vor dem Bildschirm aufgehängt, dass die Ruhelage des Pendelkörpers G in der Höhe des Kreismittelpunkts ist. Ist die Umdrehungszeit des Zeigers der Schwingungszeit des vorhandenen Federpendels angepasst, dann wird G um den Kreisradius nach unten gezogen und freigegeben, wenn der Zeiger nach unten weist. G schwingt mit der waagrechten Strecke auf und ab.
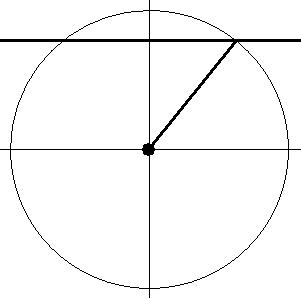
Abb. 4
Vorführung mit „12“ und „START “
Elongation, Geschwindigkeit und Beschleunigung als Funktion der Zeit
Man kann eine Schwingung mit einem rotierenden Körper K beschreiben, dessen Projektion auf die Schwingungsbahn mit dem schwingenden Körper hin und her geht. Statt eines solchen Körpers K kann man auch einen mit ω = √(D/m) rotierenden Zeiger nehmen, dessen orthogonale Projektion auf die Schwingungsbahn die Elongation anzeigt (siehe Abb.5). Die Winkelgeschwindigkeit ω des zugeordneten Zeigers heißt Kreisfrequenz.
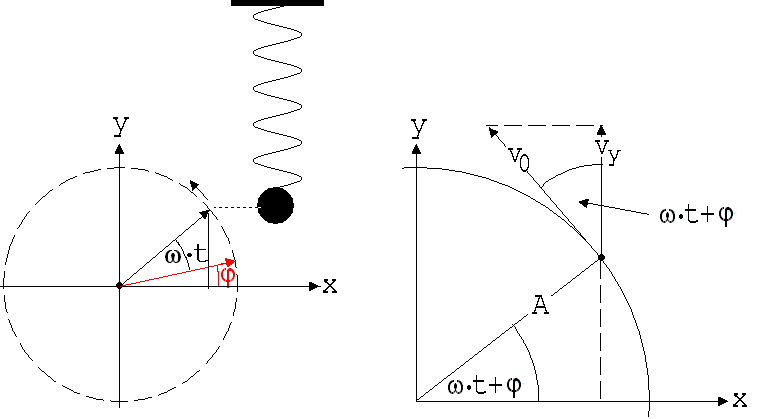
Abb. 5 Abb. 6
Wenn der mitlaufende Zeiger der Länge A den Winkel φ mit der durch den Schwingungsmittelpunkt laufenden x-Achse bildet, dann wird die Stoppuhr auf 0 gestellt. Zum Zeitpunkt t bildet der Zeiger den Winkel ω·t + φ mit der x-Achse. Für die Auslenkung y (Elongation) gilt dann:
y = A · sin(ω·t + φ); ω·t + φ heißt Phasenwinkel
Die hier aufgestellte Bewegungsgleichung gilt nur dann, wenn die beschleunigende Kraft F der Auslenkung proportional ist. Man spricht in diesem Fall von einer harmonischen Schwingung.
In der Abb. 6 ist zu sehen wie sich die Geschwindigkeit des schwingenden Körpers mit der Zeit ändert. Diese Geschwindigkeit vy erkennen wir als Vertikalkomponente der zur Zeigerspitze gehörenden Geschwindigkeit.
vy = v0 · cos(ω·t + φ); v0 = ω·A → vy = dy/dt = A ·ω· cos(ω·t + φ)
Für die Beschleunigung ay gilt: ay = - ω2·y
ay = - ω2·y; y = A · sin(ω·t + φ) → ay = dvy /dt = -A · ω2· sin(ω·t + φ)
Folgende Regeln sind erkennbar:
1. Den Differentialquotienten von einem Funktionsterm der Form „Konstante · sin(ω·t + φ)“ erhält man, indem man sin durch cos ersetzt, und den dann vorliegenden Term mit dem bei t stehenden Faktor multipliziert.
2. Differentialquotienten von einem Funktionsterm der Form „Konstante · cos(ω·t + φ) “ erhält man, indem man cos durch - sin ersetzt, und den dann vorliegenden Term mit dem bei t stehenden Faktor multipliziert.