Die Lemniskate

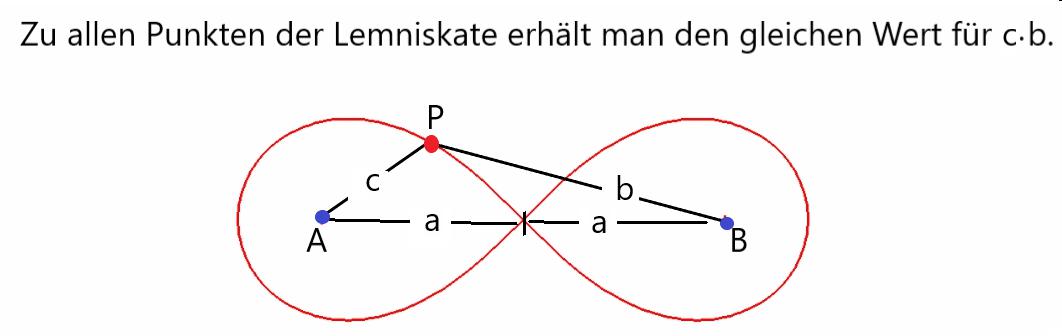
Abb. 1
Es handelt sich hier um die Lemniskate nach Bernoulli, eine Lemniskate mit einem Schnittpunkt S genau zwischen den Punkten A und B . S hat von A und B den Abstand a.
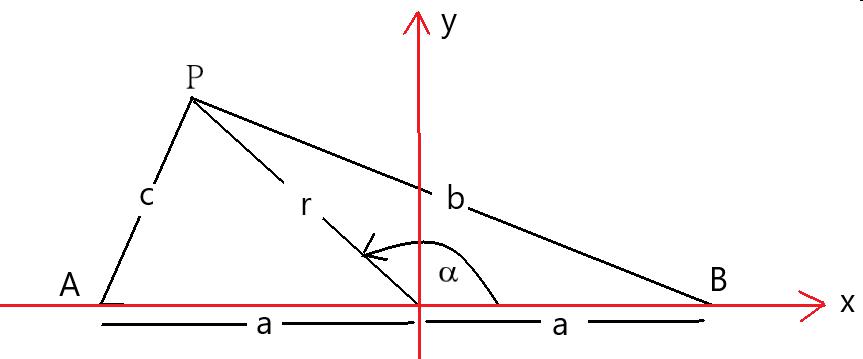
Abb.2
Der Abstand r des Punktes P vom 0-Punkt des rot dargestellten Koordinatensystems ist anhand des Winkels α bestimmbar, den die Strecke r mit der x-Achse Koordinatensystems bildet.
Es gilt nach dem Kosinussatz:
b2 = r2 + a2 – 2·r · a cos(α), c2 = r2 + a2 + 2·r · a cos(α)
cos(180- α) = - cos(α) !
b2 · c2 = a2 · a2 = (r2 + a2 – 2·r · a · cos(α)) · (r2 + a2 + 2·r · a cos(α))
a4 = (r2 + a2)2 - 4·r2 ·a2 · cos2(α)
0= r4 + 2· r2· a2 - 4·r2 ·a2 · cos2(α)
r4 = 4·r2 ·a2 · cos2(α) - 2· r2· a2 → r2 = 2· a2 · ( 2· cos2(α) -1)
1 = cos2(α) + sin2(α)
↓
r2 = 2· a2 · ( 2· cos2(α) -1) = 2· a2 · ( cos2(α) – sin2(α)) = 2· a2 · cos(2 · α)
↓
r = a · √(2 · cos(2 · α))
x = r · cos(α), y = r · sin(α)
Für die Lemniskate mit den Punkten A und B auf der y-Achse gilt:
r = a · √(2 · (- cos(2 · α)))
Mit r = a · √(2 · |cos(2 · α)|) werden beide Lemniskaten erzeugt.
Zur Dartellung einer Lemniskate