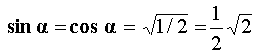Berechnung von sin-, cos- und tan - Werten zu 0°,
30°, 45°, 60°, 90°, 120° ..........
Die
sin-, cos- und tan- Werte zu den Winkeln 0°,
30°, 45°, 60°, 90°, 120° ..... können
leicht berechnet werden.
1.
α =
0°: sin α
= 0; cos
α =
1, tan α =
0
|
2.
α
=
30°:
Abb
. 1
|
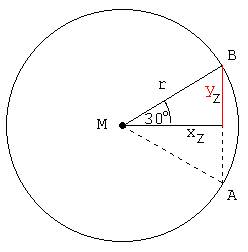
3.
α
=
45°:
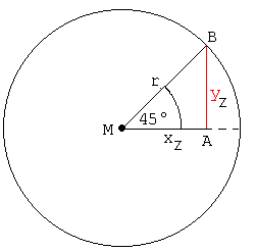
Abb.
2
|
4.
α
=
60°:
Abb.
3
|
Das
Dreieck MAB ist gleichseitig.
yz
= 0,5 · r;
xz
= 0,5 ·
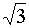 ·
r ·
r
↓
sin
α
= ½;
cos α
= ½ ·
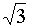
tan
α
=
1/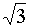
|
Das
Dreieck MAB ist rechtwinklig-gleichschenklig.
xz
= yz ;
xz2
+ yz2
= r2
2
· xz2
=
r2 ;
xz =
r ·
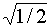
↓
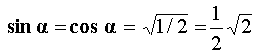
tan
α=
1
|
Das
Dreieck MAB ist gleichseitig.
yz
=
0,5 ·
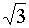 ·
r ; xz
=
0,5 · r ·
r ; xz
=
0,5 · r
↓
sin
α =
½
·
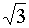 ;
cos α
= ½ ;
cos α
= ½
tan
α
=
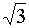
|
4.
α
=
90°:
sin
α
=
1; cos α
=
0; tan α
ist
nicht definiert
|
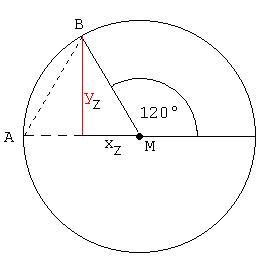
5.
α = 120°:
|
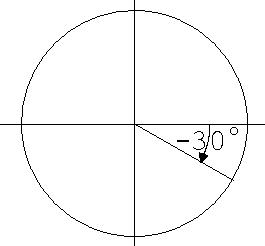
6.
α = - 30°
|
Abb.
4
|
Abb.
5
|
Das
Dreieck MAB ist gleichseitig.
yz
= 0,5 ·
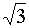 ·
r ; xz
= 0,5 · r ·
r ; xz
= 0,5 · r
sin
α =
½
·
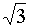 ;
cos α
= - ½;
tan α
= ;
cos α
= - ½;
tan α
=
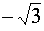
|
Diese
Rechnungen können fortgesetzt werden für 135°,
150°, 180°, 210° , - 30°, -45° usw..
Die
negativen Winkel – 30° und –45° beschreiben
Drehungen um 30° bzw. 45° im Uhrzeigersinn ( siehe
Abb.7).
sin(-30°)
= sin(330°); sin(-45°) = sin (315°) usw..
|
In
diesem Zusammenhang ist anzumerken, dass zur Berechnung von sin(α)
und cos(α) nur deren Werte im Intervall [0°; 90°]
genau erfasst werden müssen, denn zur jeder Drehung α
eines Zeigers kann immer eine Zeigerstellung mit α’ε [0°;
90°] angeben werden, so dass gilt:
|sin(α)|
= |sin(α’)|,
|cos(α)| = |cos(α’)|
Beispiele:
sin(740°) = sin(20°), sin(190°) =
-sin(10°), sin(220°) = - sin(40°),
sin(330°) = - sin(30°)
Ist der Sinus oder der Kosinus
eines Winkels bekannt, dann kann immer der Kosinus bzw. der Sinus
berechnet werden. In der Abb. 6
ist zu sehen, dass sin(α) und cos(α) durch Katheten eines
rechtwinkligen Dreiecks mit der Hypotenuse 1 dargestellt werden
können.
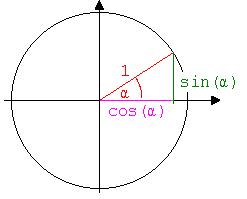
Abb.
6
[cos(α)]2
+ [sin(α)]2 = 1
Für
[cos(α)]2
und
[sin(α)]2
schreiben
wir auch cos2(α)
und sin2(α).
In
der nachfolgenden Tabelle sind die errechneten Werte in einer Tabelle
zusammengestellt.
α
Gradmaß
|
α
Bogenmaß
|
sinα
|
cosα
|
tanα
|
0°
|
0
|
0
|
1
|
0
|
30°
|
π/6
|
0,5
|
0,5
·
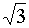
|
1/
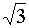
|
45°
|
π/4
|
0,5
·
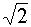
|
0,5
·
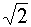
|
1
|
60°
|
2/6·
π
|
0,5
·
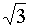
|
0,5
|
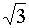
|
90°
|
π/2
|
1
|
0
|
Nicht
def.
|
120°
|
2/3
· π
|
0,5
·
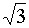
|
-
0,5
|
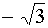
|
135°
|
¾
· π
|
0,5
·
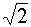
|
-0,5
·
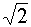
|
-1
|
150°
|
5/6
· π
|
0,5
|
-
0,5 ·
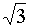
|
-
1/
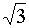
|
180°
|
π
|
0
|
-1
|
0
|
210°
|
7/6
· π
|
-
0,5
|
-0,5
·
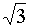
|
1/
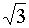
|
225°
|
5/
4 · π
|
-0,5
·
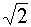
|
-
0,5 ·
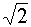
|
1
|
240°
|
4/3
· π
|
-
0,5 ·
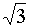
|
-
0,5
|
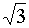
|
270°
|
3/2
· π
|
-1
|
0
|
Nicht
def.
|
300°
|
5/3
· π
|
-0,5
·
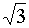
|
0,5
|
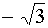
|
315°
|
7/4
· π
|
-0,5
·
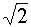
|
0,5
·
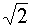
|
-1
|
330°
|
11/6
· π
|
-0,5
|
0,5
·
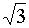
|
-
1/
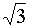
|
360°
|
2·
π
|
0
|
1
|
0
|
-30°
|
-
1/6 · π
|
-0,5
|
0,5
·
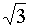
|
-
1/
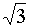
|
-45°
|
-1/4
· π
|
-0,5
·
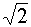
|
0,5
·
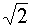
|
-1
|
-60°
|
-
1/3 · π
|
-0,5
·
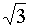
|
0,5
|
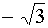
|
-
90°
|
-
π/2
|
-1
|
0
|
Nicht
def
|
Nach
Eingabe von „49“ und „START“ erscheint im
Tabellenfenster von „Mathe.-Physik“ eine Tabelle mit
gleichen Werten zur graphischen Darstellung (siehe Abb. 7).
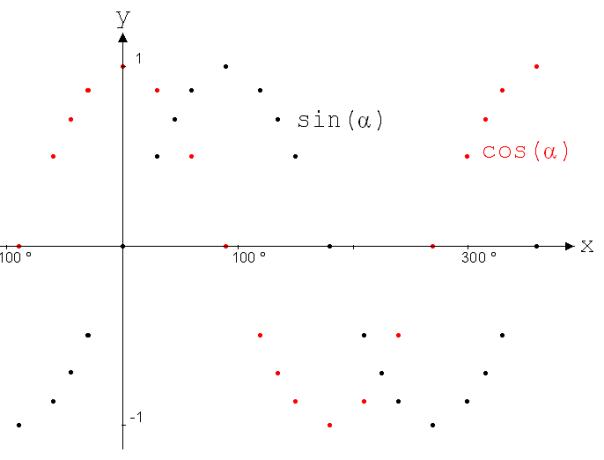
Abb.
7
In
Abb. 6 sind sin α und cos α in Abhängigkeit
von α (Gradmaß) dargestellt. y steht hier für Sin –
und Kosinuswerte und x für Winkel im Gradmaß. Die
Graphen beschreiben die Funktionen mit den Zuordnungsvorschriften y =
sin(x) und y = cos(x).
Wie
sollen die Sin- und Kosinuswerte berechnet werden, die zwischen den
in der Tabelle angegebenen Werten liegen ?
Zur
Ermittlung dieser Zwischenwerte eignen sich Polynome.