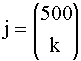
4.6 Berechnung  der Wahrscheinlichkeitsdichte für die Fehler relativer Häufigkeiten

Die Dichtefunktion zu den standardisierter Zufallsfehlern fs = (k/n – 1/6)/σ (k = Zahl der  „6“ nach n Würfen,  n = 500, 1000, 10000.., σ = Standardabweichung) kann hergeleitet werden.  Für die Herleitung müssen jedoch zunächst einige Grundgesetze der Wahrscheinlichkeitsrechnung und die zugehörenden Begriffe erläutert werden.

Wichtige Begriffe und Grundgesetze der Wahrscheinlichkeitsrechnung (anklicken !)

Nach diesem kurzen Ausflug in die Wahrscheinlichkeitsrechnung soll nun die Dichtefunktion zu  (k/n – 1/6)/σ  hergeleitet werden.

(k/n – 1/6)/σ  ist der standardisierte Fehler fs bezüglich der Wahrscheinlichkeit 1/6. 

Für die Varianz σ² gilt nach dem letzten Kapitel :    σ² = p · (1 – p)/n;     p = 1/6

Die Wahrscheinlichkeit für das Auftreten dieses Fehlers ist p(k/n).

Berechnung von p(k/n)

Wir betrachten zunächst  folgendes Ergebnis E bei n = 500 Würfen:

Die ersten k Würfe enden mit dem Ergebnis „6“, die letzten 500-k Würfe enden nicht mit einer „6“.

Die Wahrscheinlichkeit für eine „6“ als Ergebnis eines Wurfs ist p = 1/6.  Die Wahrscheinlichkeit für zwei aufeinander folgende Würfe mit  „6“ ist somit 1/6 · 1/6 = (1/6)² .  Die Wahrscheinlichkeit für k aufeinander folgende Würfe mit  „6“ ist p^k = (1/6)^k

Die Wahrscheinlichkeit für ein Wurf ≠ „6“ ist q = 5/6. 

Die Wahrscheinlichkeit für 500-k aufeinander folgende Würfe  ≠ „6“ ist q^500-k = (5/6)^500-k

→ p(E) = p^k · q^500-k

p(E) = p · p · p…….·q ·q · q · q · q …….

Das letzte Produkt beschreibt nur ein Ergebnis  E des Ereignisses  „die 6 tritt k-mal auf“. Dieses Ereignis kann auch durch ein Zufallsexperiment verwirklicht werden, welches  mit einer Zahl ≠ 6 beginnt, worauf k-mal die Zahl 6 folgt. In diesem Fall schreiben wir:

p(E) = q · p · p ·p….·q ·q · q · q .....  =  p^k · q^500-k. 

Durch Vertauschen von p und q erhält man insgesamt j Produkte, die mit gleicher Wahrscheinlichkeit auftreten. Wenn  „die 6 tritt k-mal auf“  durch j gleichwahrscheinliche Ergebnisse  realisiert werden kann, dann ist seine Wahrscheinlichkeit :

p(k/n) = j · p^k · q^500-k.

j steht für die Zahl der Anordnungen (Permutationen), die für k Buchstaben p und 500-k Buchstaben q möglich sind. Nach den Ausführungen unter „Wichtige Begriffe und Grundgesetze der Wahrscheinlichkeitsrechnung _ Anwendung auf das Lottospiel“ gilt:

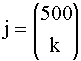
→     j = 500!/[ k! ·(500-k)!]

Wird der Würfel n-mal geworfen dann gilt:

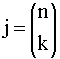
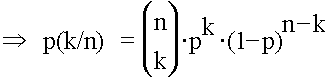
Mit p(k/n) tritt der standardisierte Fehler {k/n – 1/6}/σ auf.

m aufeinander folgende standardisierte Fehler {k/n – 1/6}/σ;  {(k+1)/n – 1/6}/σ;   {(k+2)/n – 1/6}/σ …...{(k+m)/n – 1/6}/σ werden dem Intervall [{k/n – 1/6}/σ ; {(k+m)/n – 1/6}/σ]    mit der Breite [(k+m)/n – 1/6]/σ - [k/n – 1/6]/σ = m/(n ·σ) zugeordnet. Für die Wahrscheinlichkeit, dass ein Fehler in dem genannten Intervall auftritt, kann bei geringem Unterschied zwischen k/n und (k+m)/n der Term m·p(k/n) geschrieben werden.

Die Wahrscheinlichkeitsdichte ist somit P_D = m·p(k/n) / {m/(n ·σ)} = p(k/n) · n ·σ

Unter Berücksichtigung von fs = (k/n – p)/σ    →    k = ( fs · σ + p ) · n  erhalten wir für P_D :

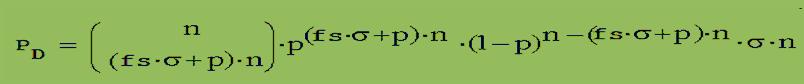
Nach dem Eintrag von  „55“ und „START“ wird „Mathe.-Physik“ zur graphischen Darstellung dieses Terms gestartet.

In der Abb.1 ist der Graph zu n = 50 und in der Abb. 2 der zu n = 1000 zu sehen. Abb. 3 ist eine Darstellung des Graphen zu n = 1000 (rot) zusammen mit dem schwarzen Graphen von f(x)=1/wrz(2·pi)*exp(-0.5*x^2) .  Es ist deutlich zu erkennen, dass P_D bei großem p·n sehr gut durch eine Exponentialfunktion beschrieben wird (lokaler Grenzwertsatz).