1.9.6 Das Frequenzspektrum einer Schwingung
Die Messung einer Frequenz f z.B. die einer schwingenden Maschine könnte wie folgt geschehen:
Eine Blattfeder mit einer auf ihr verschiebbaren schwingenden Masse G ( siehe Abb. 1) wird an M geklemmt. Hiernach beginnt sie zu schwingen. G wird solange auf der Blattfeder hin- und hergeschoben, bis die Amplitude ein Maximum erreicht. Die Eigenfrequenz der Blattfeder stimmt dann mit der Erregerfrequenz überein. Die Blattfeder ist so skaliert, dass an der augenblicklichen Stelle von G die Frequenz ablesbar ist. Hier muss angemerkt werden, dass die Federkonstante und somit auch die Eigenfrequenz der Blattfeder mit kleiner werdendem Abstand der Masse G von der Einspannstelle der Feder größer wird .

Mit dem nachfolgenden Programm soll nun untersucht werden, wie sich die Elongation der Blattfeder bei Veränderung von D ändert. Hierbei wird vorausgesetzt, dass sich D nach D = j·t ( j = Konstante) mit der Zeit ändert und dass neben der Federkraft noch eine der Elongation proportionale Reibungskraft FR = k· sgn(v)*abs(x) (abs(x) = |x|) wirkt. Außerdem wird davon ausgegangen, dass die Maschine eine Kraft nach F = 0,01· [sin(2·π·t) 1 Hz + sin(4· π·t) 2 Hz + sin(6· π ·t) 3 Hz + sin(8 · π · t) 4 Hz ] N an die schwingende Masse überträgt. Das Programm erzeugt das in der Abb. 2 sichtbare Diagramm. Es zeigt 4 Resonanzstellen an bei 1Hz, 2 Hz, 3 Hz und 4 Hz.
Anfangsbedingungen: |x|t|i|v|m|j|h|k|=|0|0|0.02|0|0.1|0.2|0.02|1|
wiederhole bis f>5
a=(-(j*t)*x-k*sgn(v)*abs(x)+ 0.01*(sin(2*pi*t)+sin(4*pi*t)+sin(6*pi*t)+sin(8*pi*t)))/m
b=a+(a-A)/2
x=0.5*b*h*h+v*h+x
v=b*h +v
A=a
f=wrz(j*t/m)/2/pi
h=i/f
Für das Zeitintervall h wird umgekehrte Proportionalität zur Frequenz f vereinbart
_f;x;;1
t=t+h
zurück
Ausführbar nach „ 204“ und „START“ .

Abb. 2
Nun wird die Kraft F = 0.01 · [sin(2·π·t) 1 Hz +sin(4· π·t) 2 Hz + sin(6· π ·t) 3 Hz + sin(8 · π · t) 4 Hz ] N durch F=0,05·[frac(t) – 0,5)] N (siehe Abb. 3) ersetzt ( frac(x) steht für den Nachkommaanteil von x ). Das Programm erzeugt hiernach das in der Abb. 4 sichtbare Diagramm.
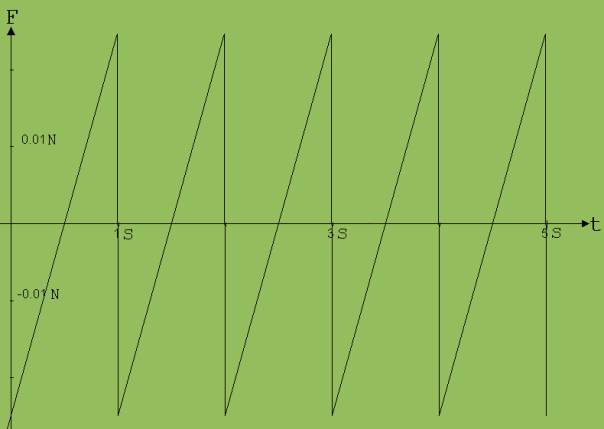
Abb. 3
|x|t|i|v|m|j|h|k|=|0|0|0.02|0|0.1|0.2|0.02|1|
wiederhole bis f>5.5
a=(-(j*t)*x-k*sgn(v)*abs(x)+ 0.05*(frac(t)-0.5))/m
b=a+(a-A)/2
x=0.5*b*h*h+v*h+x
v=b*h +v
A=a
f=wrz(j*t/m)/2/pi
h=i/f
_f;x;;1
t=t+h
zurück
Ausführbar nach „ 205“ und „START“

Abb. 4
0,05·[frac(t) – 0,5)] N verhält sich wie eine Summe aus Sinustermen.
Vermutung:
Jede periodische Funktion kann durch eine Summe von Sinustermen und einer Konstanten dargestellt werden.
Beispiel: F = 0,05·[frac(t) – 0,5)] N = K + F01 ·sin(ω·t+α1) + F02 ·sin(2·ω·t+α2) + F03 ·sin(3·ω·t+α3) +…..
Die Methode zur Auffindung dieser Sinusterme und der zugehörenden Konstanten heißt „Fourieranalyse“ .
Wenn wir die Frequenz zum 1. Sinusterm f nennen, dann ist die Frequenz des 2. Terms 2·f und die des 3. Terms 3·f. Die Schwingung mit f heißt Grundschwingung, die anderen 1. und 2. Oberschwingung usw..
Bei der Durchführung der Fourieranalyse mit dem Programm „Mathe.-Physik“ ist wie folgt vorzugehen:
Das nachfolgende Säulendiagramm ist das Ergebnis einer Fourieranalyse an F=0,05·[frac(t) – 0,5)] N . Die Höhen der Säulen sind den Werten von F01, F02 … proportional. So ist hier zu sehen, dass F02 = 0.5· F01 ist.

Abb. 5
In der Abb. 6 ist die Summe aus den ersten 60 Teilschwingungen grafisch dargestellt.
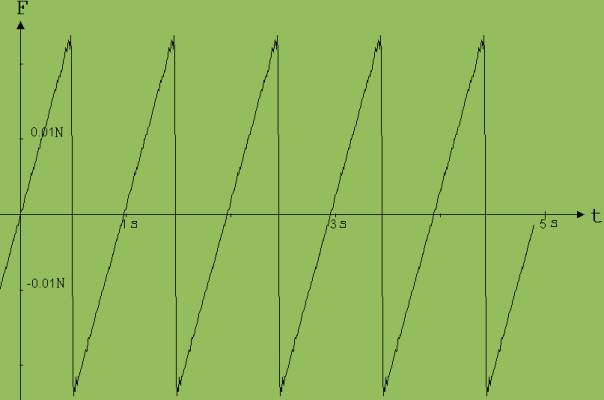
Abb. 6
0,05*[frac(t) – 0,5)] = 0.00029+0.0158 * sin( 6.28 * 1 * t + 3.09 )+0.00787 * sin( 6.28 * 2 * t + 3.053 )+ 0.00525 * sin( 6.28 * 3 * t + 3.0083 )+ 0.00389 * sin( 6.283 * 4 * t + 2.98 )+......