
1.9.3 Das Fadenpendel
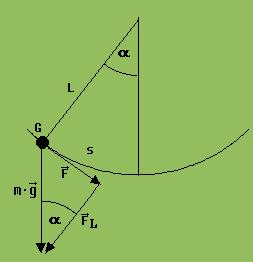
Wie in Abb. 1 erkennbar, lässt man ein Fadenpendel über der Experimentierwippe an einem Stab schwingen. Schwingt das Pendel nahe der Glasplatte, dann erhält man bei kleinen Auslenkungen ein t-s-Diagramm des schwingenden Körpers.


Abb. 1 Abb. 2
Die Schwingungszeit für kleine Amplituden kann berechnet werden ( siehe Abb. 2).
Zur Ermittlung der Schwingungszeit T wird zunächst angenommen, dass es sich um eine harmonische Schwingung handelt. Unter dieser Voraussetzung gilt:
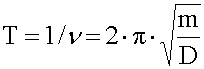
Zur Berechnung von D muss die rücktreibende Kraft F zu einer Auslenkung s bestimmt werden. Die für die Schwingung verantwortliche Erdanziehungskraft m · g verhält sich in Bezug auf den schwingenden Körper G wie ihre beiden in der Skizze angedeuteten Komponenten F und FL . F ist die rücktreibende Kraft. Für sie gilt: F = m ·g · sin α
Als Auslenkung s erhalten wir: s = L ·α (α = Winkel im Bogenmaß)
F/s = m · g · sin α / (L·α)
Die letzte Gleichung zeigt, dass es sich nicht um eine harmonische Schwingung handelt.
Beschränkt man sich jedoch auf kleine Auslenkungen s, dann kann sin α durch α ( Bogenmaß !)ersetzt werden.
F/s ≈ m·g/L
Demnach kann die Schwingung bei kleinen Auslenkungen als harmonisch bezeichnet werden.
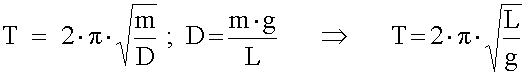
Mit dem nachfolgenden Rechenprogramm kann die Bewegung eines Pendels auch bei großen Amplituden erfasst werden.
|
Anfangsbedingungen: |x|t|h|v|g|m|L|f|d|=|0.3|0|0.0005|0|9.8|0.05|0.35|0|0.4|: Amplitude = 0,3 m |x|t|h|v|g|m|L|f|d|=|0.7|0|0.0005|0|9.8|0.05|0.35|0|0.4|: Amplitude = 0,7 m
wiederhole bis t>10 D=g*m*sin(x/L)/x a = - D*x/m b=a+(a-A)/2*f f=1 x=0.5*b*h^2+v*h+x v= b*h+v A=a t=t+h _t;x;;5 zurück
x: Auslenkung Die Amplitude ist gleich dem Anfangswert von x L: Pendellänge h : Δt
|
Wichtige Anmerkung ! Wird zur Berechnung der Änderungen von v, und x (Geschwindigkeit und Ort) während eines kleinen Zeitabschnitts h (Δt) die Beschleunigung a zu Beginn des Zeitabschnitts genommen, dann führt dies zu kleinen Fehlern, da sich die Beschleunigung innerhalb von h (Δt) ein wenig ändert. Zur Verringerung dieses Fehlers wird im Programm die Beschleunigung b in der Mitte des Zeitabschnitts h (Δt) zur Berechnung von Δx und Δv eingesetzt. Für die Änderung Δa der Beschleunigung in Δt/2 kann geschrieben werden:
Δa ≈ (avor Δt – anach Δt )/2
Da anach Δt zunächst unbekannt ist, wird das zum letzten Zeitabschnitt gehörende Δa genommen. Δa = (a – A)/2 → b = a+ (a – A)/2 A = Beschleunigung zu Beginn des letzten Zeitabschnitts der Dauer h.
Die Variable f (Anfangswert = 0) wurde eingeführt, damit a – A wegen des zunächst noch undefinierten A nicht in den ersten Rechenschritt eingeht . |
Nach der Eingabe von „27“ und „START“ kann das Programm ausgeführt werden.
In Abb. 3 sind die Diagramme zu sehen, die mit dem obigen Programm mit den Amplituden 0,3 m und 0,7 m entstehen. Es ist zu erkennen, dass bei einer großen Amplitude die Bewegung nicht mehr sinusförmig (harmonisch) verläuft und dass die Schwingungszeit größer ist als bei kleiner Amplitude.
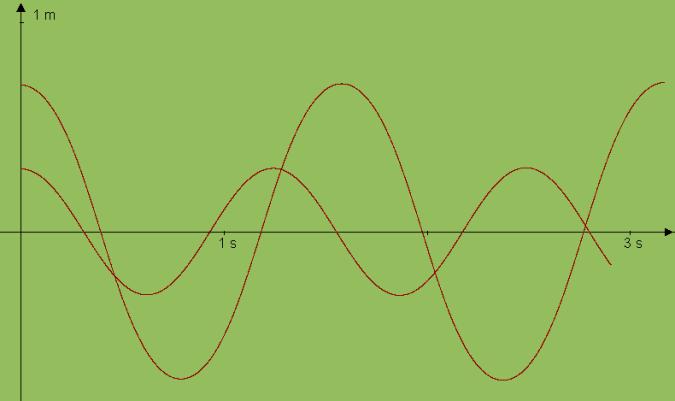
Abb. 3
Anhand der Abb. 4 soll geklärt werden, welches Signal die Wippe zur Pendelschwingung liefert.
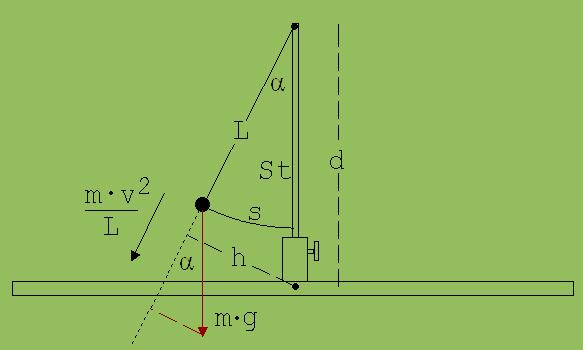
Abb. 4
Der Pendelkörper zieht an dem Stabe St mit der Gegenkraft zur Zentripetalkraft m· v2 / L
und der in Fadenrichtung wirkenden Gewichtskraftkomponenten m·g · cos (α).
Beide Kräfte bewirken zusammen das Drehmoment M = (m· v2 / L + m·g · cos (α)) · h ; h = d · sin(α)
→ M = [m· v2 / L + m·g · cos (α)] · d · sin(α)
Bei kleinen Winkeln α kann cos(α) gleich 1 und sin(α) = s/L gesetzt werden. m· v2 / L kann bei kleinen Ausschlägen gegenüber m · g · cos(α) vernachlässigt werden.
→ M = m·g·d/L · s → M ~ s
Dieses M wird vom Rechner angezeigt.
→ Nur bei kleinen Winkeln ist die Anzeige des Rechners der Auslenkung s proportional.
Ist außerdem L ≈ d dann folgt: M = m·g · s
Das Moment ist so, als ob der Pendelkörper auf der Glasplatte hin und her rutscht.
|
|x|t|h|v|g|m|L|f|d|=|0.05|0|0.0005|0|9.8|0.05|0.35|0|0.4|: Amplitude = 0,05 m |x|t|h|v|g|m|L|f|d|=|0.1|0|0.0005|0|9.8|0.05|0.35|0|0.4|: Amplitude = 0,1 m
wiederhole bis t>10 D=g*m*sin(x/L)/x a = -D*x/m b=a+(a-A)/2*f f=1 x=0.5*b*h^2+v*h+x v= b*h+v A=a t=t+h M = (m*v^2/L+m*g*cos(x/L))*d*sin(x/L) _t;M;;5 zurück
x: Auslenkung Die Amplitude ist gleich dem Anfangswert von x L: Pendellänge h : Δt |
Mit dem nebenstehende Programm wird das Drehmoment M während der Schwingung in Abhängigkeit von der Zeit dargestellt. Nach „177“ und „START“ kann dieses Programm ausgeführt werden und liefert dann die Diagramme in der folgenden Abbildung. Bei einer 5 cm-Amplitude (8,2° Auslenkung) kann das Diagramm noch als sinusförmig bezeichnet werden (M ~ s), nicht jedoch bei einer 10cm -Amplitude.
Abb. 5
|