1.3.7 Momentangeschwindigkeit und Beschleunigung

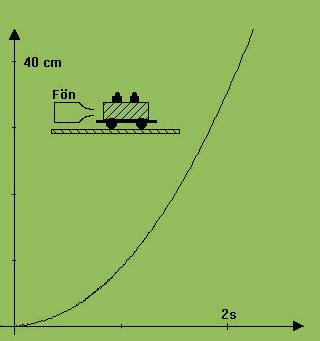
Abb. 1
1. Die Momentangeschwindigkeit
In Abb. 1 sehen wir einen Experimentierwagen auf der Experimentierwippe, der durch den Luftstrom eines Fönes angetrieben wird. Solange der Wagen unter der Einwirkung eines Luftstroms steht, hat das zugehörende t-s- Diagramm einen gekrümmten Verlauf . Der Wagen wird fortwährend schneller.
Kann man an einem solchen Diagramm Geschwindigkeiten bestimmen ?
In 1.3.6 wurde zur Ermittlung der Geschwindigkeit der Luftstrom zum Wagen hin unterbrochen und so eine gleichförmige Bewegung mit der Geschwindigkeit v herbeigeführt. Dieses v wurde als Momentangeschwindigkeit zum Zeitpunkt t, dem Zeitpunkt der Unterbrechung angegeben. Es ist die Geschwindigkeit, die der Wagen beibehält, wenn nach t keine Kraft auf ihn einwirkt. Nun erscheint folgendes Vorgehen angemessen:
Der Weg Δs in einem auf den Zeitpunkt t folgenden kleinen Zeitabschnitt Δt wird bestimmt. Δt wird so klein gewählt, dass sich in dieser kurzen Zeit die Kraft nur wenig auf die Bewegung auswirken kann und infolgedessen Δs/Δt kaum von der Geschwindigkeit v abweicht, die sich einstellt, wenn nach t keine Kraft wirkt. Die Abweichung |Δs/Δt – v| strebt mit kleiner werdendem Δt gegen 0. Man sagt in diesem Fall, v ist der Grenzwert von Δs/Δt für Δt → 0. An der Bilderserie in Abb.2 ist die Entwicklung zu dem genannten Grenzwert v zu erkennen. Durch Anfang und Ende der zu kleinen Zeitabschnitten Δt gehörenden Kurvenabschnitten, die unmittelbar auf den Zeitpunkt t = 1 s folgen, werden Geraden gelegt. Die Steigung einer Geraden ist gleich dem Quotienten Δs/Δt. Mit kleiner werdendem Δt streben die Geraden gegen eine Grenzlage. Eine Gerade in dieser Grenzlage wird Tangente (Berührungsgerade ) genannt, ihre Steigung ist gleich der Momentangeschwindigkeit v.
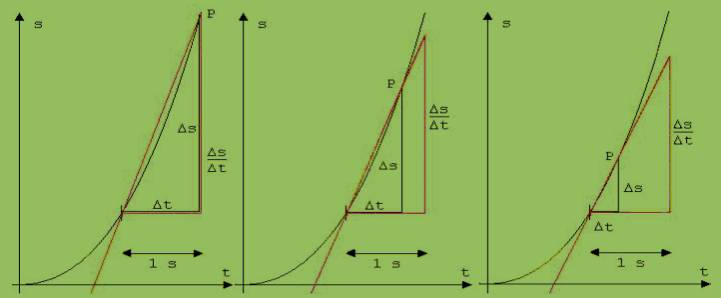
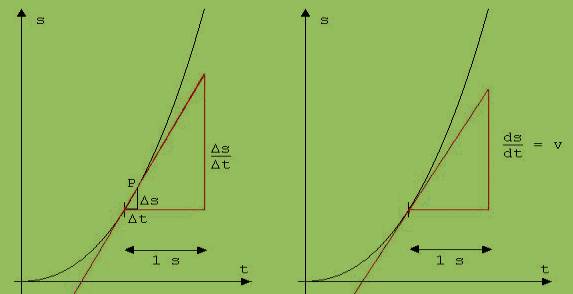
Abb. 2
Für den Grenzwert von Δs/Δt schreibt man lim Δs/Δt ( Δt → 0) oder ds/dt ( sprich ds nach dt). Mit der Sprechweise ds nach dt anstelle von ds durch dt soll vermieden werden, dass dieser Grenzwert (Differenzialquotient) als Quotient bestimmter Größen aufgefasst wird. Lim ist eine Abkürzung für Limes (Grenze).
Als Momentangeschwindigkeit v zu einem bestimmten Zeitpunkt t definieren wir nun den Grenzwert von Δs/Δt.
v = lim Δs/Δt ( Δt → 0) = ds/dt
Berechnung der Momentangeschwindigkeit
Man kann wohl davon ausgehen, dass erst der Weg s berechenbar sein muss, bevor dies für die Momentangeschwindigkeit v möglich ist. Deshalb soll eine Gleichung (Formel) der Form s = f(t) gesucht werden, die es ermöglicht, den Weg s nach einer Beschleunigungszeit t zu berechnen. Möglicherweise besteht eine Proportionalítät zwischen mittlerer Geschwindigkeit und der Zeit. Unter einer mittleren Geschwindigkeit vm verstehen wir das Verhältnis aus einem zurückgelegten Weg s und der zugehörenden Zeit t. Diese Definition ist an keinen besonderen Bewegungsablauf geknüpft; die Bewegung kann in der Zeit t langsamer oder schneller werden.
vm = s/t
Zur Prüfung der vermuteten Proportionalität werden am Diagramm der Abb. 1 zu verschiedenen Zeitpunkten t ( t: Zeit seit Beginn der Bewegung ) die zurückgelegten Wege s abgelesen und in eine Tabelle eingetragen. Wir erkennen, dass die Vermutung zutrifft. Die geringen Schwankungen in der letzten Spalte sind auf Messfehler zurückzuführen.
|
t |
s |
vm = s/t |
vm /t = s/t2 |
|
0,35 s 0,73 s 0,98 s 1,25 s 1,48 s 1,71 s 1,98 s 2,23 s |
1,4 cm 5 cm 8,6 cm 14 cm 19,3 cm 26 cm 35 cm 45 cm |
4 cm/s 6.8 cm/s 8,77 cm/s 11,2 cm/s 13 cm/s 15,2 cm/s 17,7 cm/s 20,2 cm/s |
11,42 cm/s2 9,38 cm/s2 8,95 cm/s2 8,96 cm/s2 8,81 cm/s2 8,89 cm/s2 8,92 cm/s2 9,05 cm/s2 |
↓
s/t2 = 8.9 cm /s2 = 0,089 m/s2 = k (Konstante) → s = k · t2
Nun kann sehr genau gezeigt werden, wie sich Δs/Δt mit kleiner werdendem Δt entwickelt. Die nebenstehende Tabelle enthält Δs- und Δs/Δt-Werte zu verschieden großen Zeitabschnitten Δt, die sich an t = 1 s anschließen. Sie wurden mit s = k · t² (k=8,9 cm/s2 ) berechnet. Es ist zu erkennen, dass Δs/Δt mit kleiner werdendem Δt einem Grenzwert zustrebt.
Berechnungsbeispiel für Δt = 0,1 s : Δs = 8,9 cm/s2 · (1,1 s)2 - 8,9 cm/s2 · (1 s)2 = 1,869 cm
|
Δt |
Δs |
Δs/Δt |
|
0,1 s 0,01 s 0,001 s 0,0001 s 0,00001 s |
1,869 cm 0,17889 cm 0,017808 cm 0,00178008 cm 0,00017800089 cm |
18,69 cm/s 17,889 cm/s 17,808 cm/s 17,8008 cm/s 17,800089 cm/s |
Die Momentangeschwindigkeit zum Zeitpunkt t = 1 s ist 17,8 cm/s.
17,8 cm/s = 2 ·k · 1 s
Vermutung: vzum Zeitpunkt t = 2 · k · t
Beweis:
s = k · t2
↓
Δs in der Zeit Δt = k ·(t+Δt)2 - k· t2 → Δs/ Δt = [ k ·(t+Δt)2 - k· t2 ] / Δt
↓
Δs/ Δt = [k ·( t2 + 2·t· Δt + Δt2) – k · t2 ] / Δt → Δs/ Δt = 2 · k ·t + k · Δt
Mit kleiner werdendem Δt strebt k·Δt gegen 0.
↓
v = ds/dt = lim Δs/Δt ( Δs → 0) = 2·k·t
Wie verhält sich die Momentangeschwindigkeit zur mittleren Geschwindigkeit ?
Für die mittlere Geschwindigkeit vm während des Zeitabschnitts Δt gilt:
vm = Δs/ Δt = [k· (t+Δt)2 - k·t2 ] / Δt = k·2 ·t + k · Δt = k·t + k · (t +Δt)
k·t und k · (t +Δt) sind die halben Momentangeschwindigkeiten zu den Zeitpunkten t und t +Δt.
vm = vvor Δt / 2 + vnach Δt / 2 = (vvor Δt + vnach Δt)/2
Die mittlere Geschwindigkeit in einem Zeitabschnitt Δt ist gleich dem Mittelwert aus der Anfangs- und Endgeschwindigkeit.
2. Die Beschleunigung
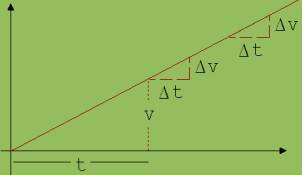
Abb. 3
Untersuchung einer gleichförmig-beschleunigten Bewegung mit der vorliegenden On-Line-Stoppuhr
In Abb. 3 sehen wir v = 2 · k · t in Abhängigkeit von der Beschleunigungszeit t. Der mit dem Namen Beschleunigung a (acceleration) belegte Quotient Δv / Δt beschreibt die Änderung der Geschwindigkeit in einer Zeiteinheit.
Für eine Bewegung nach s = k· t2 gilt: v/t = Δv/Δt = 2 ·k
a = 2 · k → s = ½ · a · t2
Bei der Bewegung nach s = k·t2 ist die Beschleunigung konstant (a = k ·2 ). Man spricht in diesem Fall von einer gleichförmig - beschleunigten Bewegung. In gleichen Zeiten erfährt das bewegte Objekt gleiche Änderungen seiner Geschwindigkeit.
Wichtige Anmerkung: Der oben angegebene Satz „Die mittlere Geschwindigkeit ist der Mittelwert aus der Anfangs- und Endgeschwindigkeit“ gilt nur bei einer gleichförmig - beschleunigten Bewegung.
Kraft und Beschleunigung
Nach Kenntnis der Beschleunigung kann die beschleunigende Kraft berechnet werden:
F = Δ(m·v)/Δt
Ist m konstant, dann gilt: F = m· Δv/Δt → F= m· a
Beispiele für gleichförmig-beschleunigte Bewegungen
Es stellt sich die Frage, welche der uns bekannten Bewegungen als gleichförmig-beschleunigt anzusehen sind. Wir denken hierbei an eine auf einer schiefen Ebene herab rollende Kugel und einen fallenden Körper. Wir werden nun beide Bewegungen daraufhin untersuchen und in beiden Fällen eine gleichförmige Beschleunigung feststellen.
1. Bewegung auf einer schiefen Ebene (Zeiterfassung mit Mausklick)
2. Der Freie Fall (Gewichtskraft)
Ausflug in die Differentialrechnung