Von einer harmonischen Schwingung spricht man, wenn die zur Ruhelage treibende Kraft F der Auslenkung x proportional ist (F = D · x , D=Konstante). Die Bewegung eines harmonisch schwingenden Körpers wird durch eine Sinusfunktion beschrieben.
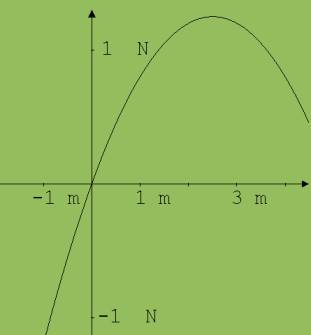
Bewegt sich ein schwingender Gegenstand unter einer Kraft, die einem anderen Gesetz folgt, dann hat man eine anharmonische Schwingung. Wir untersuchen nun das Verhalten eines Körpers der Masse m, der unter der Kraft F = (1-0,2·x)·x schwingt. Die Abhängigkeit der Kraft F von der Auslenkung x sehen wir in der Abb.1. Die zurücktreibende Kraft nimmt bei einer Bewegung nach links erheblich stärker zu als bei einer Bewegung nach rechts. Eine solche Asymmetrie der Kraft ist in der Natur häufig zu finden. Man denke z.B. an schwingende Atome an der Oberfläche eine Körpers. Schwingen diese Atome in den Körper hinein, dann erfahren sie Abstoßungskräfte von anderen Atomen. Derartige Abstoßungskräfte fehlen beim Schwingen nach außen. Somit steigt die zurücktreibende Kraft beim Schwingen nach außen weniger stark an als beim Schwingen in die Gegenrichtung.

Abb. 1
Die Bewegung unter der Kraft F = (1-0,2·x)·x [D = F/x = 1-0,2·x ] kann leicht mit Hilfe des folgenden Rechenprogramms untersucht werden.
|x|t|h|v|m|u|=|4|0|0.002|0|1|0|: Anfangsbedingungen
wiederhole bis t>20
D=(1-0.2*x)
a= -D*x/m
b = a+(a-A)/2*f
f=1
x=0.5*b*h^2+v*h+x
v=b*h+v
A=a
t=t+h
_t;x;;1
zurück
Zur Ausführung des Programms muss nach dem Eintrag von „26“ die Starttaste angeklickt werden.
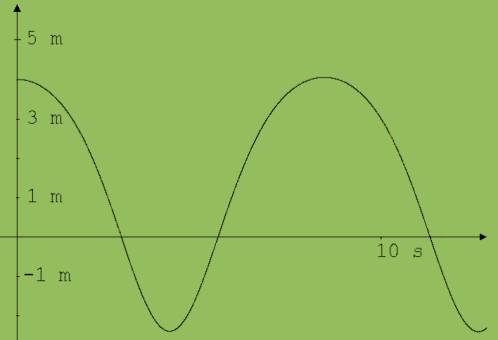
Besonders auffallend an dem mit diesem Programm geschriebene Bewegungsdiagramm (siehe Abb. 2), ist die Tatsache, dass der Schwingungsmittelpunkt nach der Seite verschoben wird, von der aus die geringeren Gegenkräfte kommen. Diese Verschiebung nimmt mit steigender Amplitude zu. Hiermit wird die Ausdehnung von Gegenständen bei Erwärmung verständlich. Die Schwingungsmittelpunkte der nahe der Oberfläche schwingenden Atome rücken mit wachsender Amplitude (steigender Temperatur) nach außen. Der Rechner findet mit dem Unterprogramm „Mathe._Fourieranalyse“ den folgenden Funktionsterm für das Diagramm in Abb. 2:
f(t) = 1.44320712694878+3.13605992462422 * sin( 0.739687159178546 * 1 * t + 1.60929972958759 )+ 0.587973273942094 * sin( 0.739687159178546 * 2 * t + 4.81212208049865 )+ 0.0712694877505568 *sin(0.739687159178546 * 3 * t + 1.72039597696584 )
Bei der Durchführung der Fourieranalyse mit dem Programm „Mathe.-Physik“ ist wie folgt vorzugehen: