1.4.2   Bewegung unter einer dem Betrage nach konstanten Normalkraft

Wenn eine Kraft auf einen Körper K einwirkt,  erwartet man an K eine Veränderung des Geschwindigkeitsbetrages. Dies ist nicht immer der Fall, z.B. dann nicht, wenn es sich um eine Normalkraft handelt, eine Kraft die orthogonal zur Bewegungsrichtung wirkt. Man denke an einen Körper, der an einem Faden auf einer Kreisbahn geführt wird. Wir untersuchen nun eine Bewegung in der x-y-Ebene unter einer dem Betrage nach konstanten Normalkraft F = m × {F₁ ; F₂ ; 0}. In der Schule ist die mathematische Behandlung dieser Bewegung nur mit Hilfe eines Rechners möglich. Hierbei wird in folgender Weise vorgegangen: Die Bewegungszeit wird in sehr kleine Zeitabschnitte Δt = h zerlegt. Ein h ist so klein, dass innerhalb dieses Abschnitts die Kraft als konstant angesehen werden kann. Mit den für konstante Kraft geltenden Bewegungsgleichungen wird die Orts- und Geschwindigkeitsänderung während des ersten Zeitabschnitts h unter Berücksichtigung der für h geltenden Kraft berechnet.

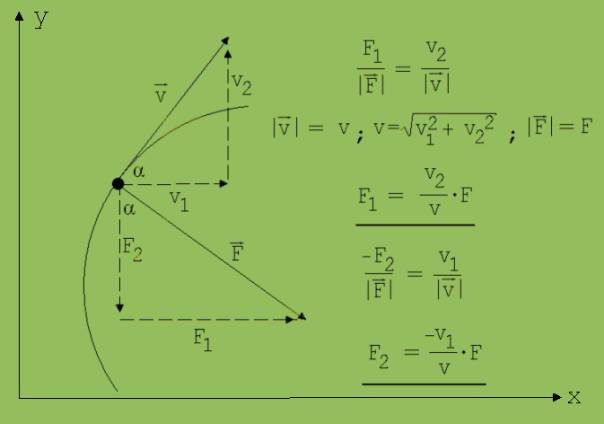
Nach dieser Rechnung ist der Ort und die Geschwindigkeit zu Beginn des zweiten Abschnitts h bekannt. Mit diesen Werten wird daraufhin der Ort und die Geschwindigkeit zu Beginn des dritten Abschnitts berechnet usw. Die Koordinaten F₁ und F₂ der Kraft F (|F| = F) werden wie folgt bestimmt:

Abb. 1

Mit der nachfolgenden Programmzeile, ausführbar mit dem hier vorhandenen Online-Grafikprogramm , kann die Bewegung unter einer Normalkraft simuliert werden (siehe Abb. 2).

k=0,5; h=0,01; m=1; i=wrz(c^2+d^2); f=k*d/i; g=-k*c/i; a=f/m; b=g/m; x=0,5*a*h^2+c*h+x; y=0,5*b*h^2+d*h+y ; c=c+a*h; d=d+b*h; l=l+1; t=t+h

k = F , f = F₁, g = F₂ , a = a₁, b = a₂ , c = v₁, d =v₂, i = v; h = Δt

Mit dieser Zeile wurde die Bahn in der Abb.2 erhalten. Im Variablenfeld wurde für v₁ = c der Wert 1,5 (1,5 m/s) , für F = k der Wert 0,5 (0,5 N) und für den Anfangswert von y die Zahl 4,5 (4,5m) eingetragen. Mit der Eingabe n =1886 wurde festgelegt, dass die eingetragene Zeile 1886 Mal bearbeitet wird, dass somit 1886 Punkte gezeichnet werden. Die Bearbeitung wird beendet wenn l (L) in der Programmzeile größer als n ist.

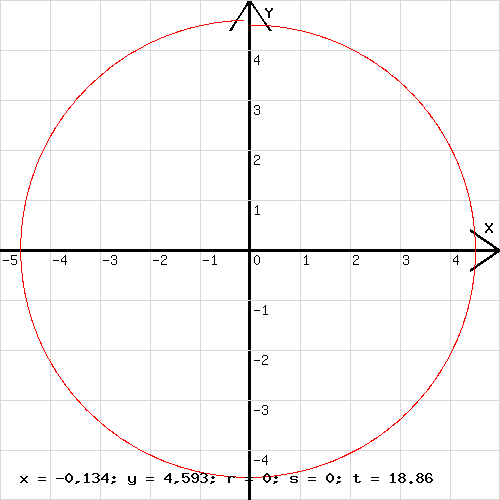
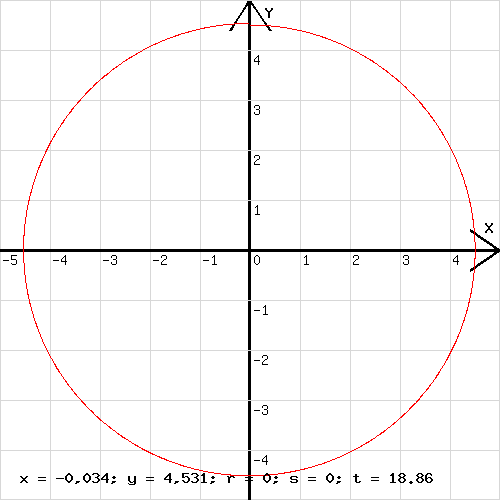
Abb. 2                                                             Abb. 3

Die in der Abb. 2 sichtbare Bahn weicht etwas von einer Kreisbahn ab. Dies ist auf Rechenungenauigkeiten zurückzuführen. Eine höhere Rechengenauigkeit wird erreicht, wenn zur Berechnung statt der Beschleunigung zu Beginn eines kleinen Zeitabschnitts Δt die Beschleunigung in der Mitte von Δt genommen wird. Für die Änderung Δa der Beschleunigung in Δt/2 kann geschrieben werden:

Δa ≈ (a_nach Δt – a_vor Δt ) / 2 → a_Mitte ≈ a_{vor Δt} + (a_{nach Δt} – a_{vor Δt} ) / 2

Da a_{nach Δt} zunächst unbekannt ist, ist eine solche Korrektur für das erste Δt nicht möglich. Für die folgenden Zeitabschnitte werden die Δa - Werte genommen, die für den jeweils vorangehenden Zeitabschnitt ermittelt wurden. Dies geschieht mit der folgenden Anweisungen an den Rechner:

k=0,5; h=0,01; m=1; i=wrz(c^2+d^2); f=k*d/i; g=-k*c/i; a=f/m; b=g/m; a=0,5*j*(a-o)+a;b=0,5*j*(b-p)+b; x=0,5*a*h^2+c*h+x; y=0,5*b*h^2+d*h+y ; c=c+a*h; d=d+b*h; o=a;p=b; l=l+1; j=1; t=t+h

Mit a = 0,5 * j * (a - o) + a; b = 0,5 * j * (b - p) + b; wird die Korrektur vorgenommen. o und p sind Beschleunigungen zu Beginn des vorangehenden Zeitabschnitts Δt. Da solche Werte beim ersten Δt nicht vorliegen, müssen 0,5 * (a – o) und 0,5 * (b - p) zuallererst unberücksichtigt bleiben. Dies gelingt mit der Variablen j, die zunächst den Wert 0 hat, dann aber nach der ersten Berechnung auf 1 gesetzt wird. In der Abb.3 ist eine Kreisbahn zu sehen, die mit dieser Korrektur gezogen wurde.

Die auf den Kreismittelpunkt gerichtete Normalkraft heiß Zentripetalkraft. Der Kreisradius r ist von dieser Kraft F als auch von der Masse m und der Geschwindigkeit v des rotierenden Teilchens abhängig. Für r kommt ein Term mit m, v und F in Frage, dessen Einheit eine Längeneinheit ist. Vermutung: r = m ·v² / F . Werden zu verschiedenen Werten von m, v und F Kreisbahnen gezeichnet, dann erfährt diese Vermutung eine Bestätigung.

r = m ·v² / F → F = m ·v²/r

Berechnung der Zentripetalkraft