1.12.3 Winkelbeschleunigung und Drehmoment
Aufgabe:
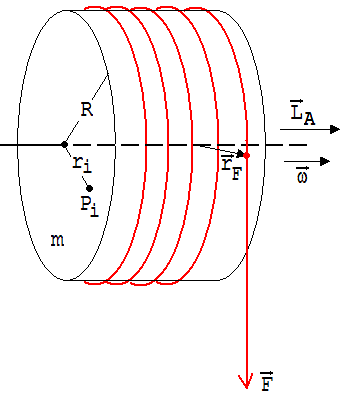
Ein m = 500 g schwerer Zylinder (R = 4 cm) kann sich reibungsfrei um eine waagrechte Achse drehen (siehe Abb. 1). Um diesen Zylinder ist ein 2 m langer Faden gewunden, der mit der Kraft 1 N vom Zylinder abgezogen wird.
Wir ändert sich die Winkelgeschwindigkeit unter der Einwirkung der Kraft F ?
Nach welcher Zeit ist der 2m lange Faden abgespult ?

Abb. 1
Berechnung des Drehimpulses
Die in Achsenrichtung weisende Drehimpulskomponente LA des Zylinderdrehimpulses ändert sich unter dem parallel zur Achse wirkenden Drehmoment der Kraft F. Zur Beantwortung der gestellten Fragen muss deshalb LA als Funktion der Winkelgeschwindigkeit ω dargestellt werden. Hier ist ω fett gedruckt, womit darauf hingewiesen wird, dass ein Vektor gemeint ist. Unter dem Vektor ω der Winkelgeschwindigkeit verstehen wir einen Vektor parallel zur Drehachse, dessen Betrag mit der bekannten Winkelgeschwindigkeit ω übereinstimmt. Die Richtung von ω ist so festgelegt, dass ein Beobachter eine Linksdrehung wahrnimmt, wenn ω auf ihn zeigt.
Zunächst suchen wir eine solche Beziehung für einen einzigen Massepunkt Pi des Zylinders, der sich im Abstand ri von der Achse befindet. Seinen Drehimpuls Li in Bezug auf einen Achsenpunkt B erhalten wir nach:
Li = rBi x mi ·vi = (rB + ri) x mi ·vi = rB x mi ·vi + ri x mi ·vi
rBi ist der von dem Punkt B ausgehende Ortsvektor von Pi. rB zeigt von B zu dem Achsenpunkt, um den Pi kreist. rB x mi ·vi bildet mit der Drehachse einen rechten Winkel. ri x mi ·vi = LAi ist die Komponente des Drehimpulses Li in Achsenrichtung.
|LAi| = ri · mi ·vi ; vi = ω · ri → |LAi| = ω · mi · ri2 → LAi = ω · mi · ri2
Der Drehimpulskomponente LA des Zylinders ist gleich der Summe aller LAi.
Da sich die zur Achse senkrecht stehenden Komponenten der verschiedenen Li aus Symmetriegründen gegenseitig aufheben ist LA der Gesamtdrehimpuls L des Zylinders.
LA = ω ·(m1 · r12 + m2· r22 + m3· r32 ..)
Die Summe m1· r12 + m2· r22 + m3· r32 .. ist als Trägheitsmoment J bekannt.
LA = ω · J; JZylinder der Masse m = ½· m · R2
↓
LA = ω · ½ · m · R2
Für die Änderung von LA ist das Moment MA = rF x F maßgebend. MA ist die zur Achse A parallele Komponente des Drehmoments M . rF ( |rF| = R ) ist ein senkrecht zur Rotationsachse stehender Ortsvektor von einem Achsenpunkt zum Angriffspunkt der Kraft (siehe Abb. 1. 12.8 ).
|MA| = R· F → R· F = dLA /dt = J · dω/dt ; ω = | ω|; LA = |LA| !
dω/dt = aα heißt Winkelbeschleunigung.
ω = v / R → dω/dt = (dv/dt)/ R = a/ R ; v = |v|, a = |a|
a beschreibt sowohl die Beschleunigung des Zylindermantels als auch die des Fadens.
Wie bewegt sich der Faden ?
R· F = J · dω/dt = J · a/R → a = F · R2 / J
Der Faden bewegt sich nach s = ½·a· t2.
s = ½ ·(F · R2 / J) · t2 → t2 = 2· s · J / (F · R2 ); J = ½· m · R2
t2 = s · m / F → t2 = 2 m · ½ kg / 1 N = 1 s2 → t = 1 s
Die hier gestellte Aufgabe kann auch mit Hilfe des Energiesatzes gelöst werden. Die kinetische Energie des Zylinders J·ω2/2 nach dem Abspulen des Fadens ist gleich der am Faden verrichteten Arbeit s·F.
s·F = J·ω2/2 ; ω = v / R → s·F = J· [v2 / R2]/2
v = 2·(s/t); v = 2· mittlere Geschwindigkeit !
s·F = J· 4· [(s/t)2 / R2] /2 → t2 = 2·J·s /(R2 · F); J = ½· m · R2 → t2 = s · m / F
Es fällt auf, dass man den Gesetzen der Punktmechanik (Schwerpunktmechanik) zur Drehbewegungen passende Gesetze zuordnen kann, indem man v durch ω, m durch J, m·v durch L und F durch M ersetzt.
|
s = |v|· t |
→ |
α = |ω| · t |
|
p = m·v |
→ |
L = J · ω |
|
F = m· dv/dt |
→ |
M = J ·dω/dt |
|
E = m·v2 /2 |
→ |
E = J· ω2 / 2 |
L = J · ω ist nicht allgemein gültig, denn L kann eine andere Richtung haben als ω. Haben L und ω gleiche Richtungen, dann nennt man die Rotationsachse eine Hauptträgheitsachse. Es gibt zu jedem Körper mindestens drei derartige durch den Schwerpunkt laufende Hauptträgheitsachsen, die senkrecht zueinander stehen (siehe Abb. 2).
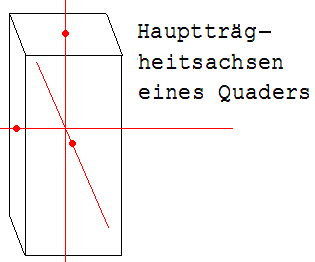
Abb. 2
Drehmomente bei einer Richtungsänderung des Vektors L
Nach L = J·ω ändert sich der Drehimpuls auch dann, wenn ω eine andere Richtung annimmt. Auch in diesem Fall ist mit einem Drehmoment zu rechnen. Zum Nachweis eines solchen Drehmoments dient das in der Abb.3 sichtbare Instrument, es ist unter dem Namen „Pendelkreisel“ erhältlich. Am unteren Ende eines schwingenden Pendels (variable Winkelgeschwindigkeit des Pendels = ω’) rotiert ein 420 g schwerer Zylinder mit der Winkelgeschwindigkeit ω um die Achse eines Elektromotors. Wenn man den Halter des Pendels nicht fest in die Hand nimmt, dann weicht das Pendel quer zur Schwingungsebene aus (weißer Pfeil) und dreht hierbei den Haltegriff. Ein Drehmoment M ( im Sinne einer Drehung gegen den weißen Pfeil) ist erforderlich, wenn die Rotationsachse des Zylinders in der Schwingungsebene bleiben soll.

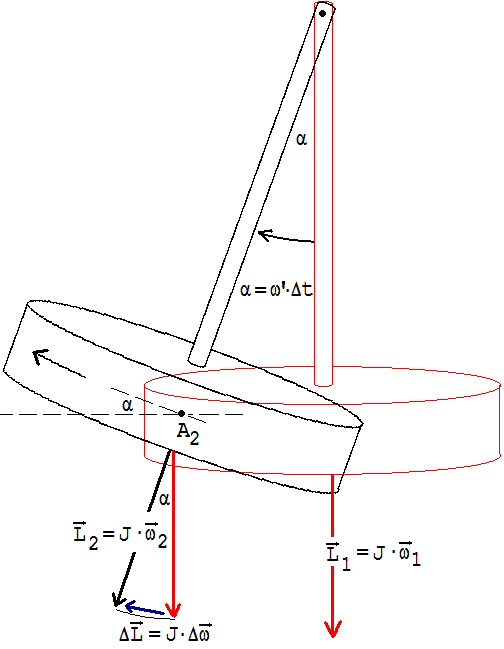
Abb. 3 Abb. 4
In Abb. 4 ist der dem Betrage nach konstante Drehimpuls J·ω in Achsenrichtung des Zylinders vor und nach einer kleinen Zeit Δt durch
L1 = J·ω1 und L2 = J·ω2 dargestellt.
| J·ω1 | = | J·ω2 | = J · ω
|ω| = ω
|ΔL| / (J · ω) = α (Bogenmaß)
α = ω’ · Δt
↓
|ΔL| = ω’ · Δt · J·ω
↓
|M| = M = |ΔL| / Δt
|M| = ω’ · Δt · ω·J / Δt = ω’ · ω ·J
Schwingt das Pendel auf einen links stehenden Beobachter zu, dann ist aus dessen Sicht zur Vermeidung einer Rechtsdrehung ein Drehmoment M (M = |M| ) im Sinne einer Linksdrehung erforderlich. Nach dem Wechselwirkungsgesetz übt das Pendel auf die haltende Hand ein gleich großes Gegenmoment M’ (M’ = |M’| ) aus.
Zur Messung des Gegenmoments M’ lässt man das Pendel genau über der Achse der Wippe schwingen. Während der Schwingung wird ein Diagramm gezeichnet, welches dem einer Schwingung ähnelt. Es zeigt eine Drehung der Wippe an, die von der zur Achse parallelen Komponente des Vektors Mʼ verursacht wird. Beim Schwingen durch die Ruhelage erfährt die Wippe ihren maximalen Ausschlag. Mʼ ist in diesem Fall parallel zur Drehachse der Wippe, gleicht deshalb dem Drehmoment der Rückstellfeder und kann anhand der am Diagramm ablesbaren Drehung der Wippe bestimmt werden.

Abb. 5
Zur Messung ist Folgendes anzumerken:
Das durch die Rückstellfeder aufgebrachte Drehmoment ist nicht das gesamte auf die Wippe wirkende Moment. Zur Begründung ist Folgendes zu sagen: Der Drehimpuls eines Körpers K in Bezug auf irgendeinen Raumpunkt D ist gleich der Summe aus dem Drehimpuls LP in Bezug auf den Schwerpunkt und dem Drehimpuls LS des Schwerpunkts.
Lg = LS + LP
Der Zylinder dreht sich nicht nur um die Motorachse, sondern infolge der Pendelbewegung auch noch um eine zur Schwingungsebene senkrechte Hauptträgheitsachse A2 (siehe Abb. 1.12.11). Infolgedessen ist LP eine Summe aus ω ·J und einem durch ω’ bedingten Anteil L’.
Lg = LS + (ω ·J + L’ )
Wir betrachten die Glasplatte der Wippe mit dem Pendelkreisel als ein System S. Der Bezugspunkt D des Drehimpulses liege auf der Drehachse der Wippe. In diesem Fall hat L’ + LS keinen Einfluss auf die Drehung der Wippe, weil L’ + LS mit der Wippenachse einen rechten Winkel bildet. Dies gilt auch für die Änderung dieser Summe und des daraus resultierenden Moments. d(J·ω)/dt ist für die Drehung der Wippe maßgebend. Die zur Wippenachse parallele Komponente von d(J·ω)/dt wird von der Rückstellfeder aufgebracht. Beim Durchschwingen der Ruhelage stimmt diese mit d(J·ω)/dt überein.
Auch das Drehmoment des Elektromotors beim Beschleunigen des Zylinders kann mit der Experimentierwippe gemessen werden. Der Pendelkreisel wird so an der Wippe befestigt, dass die Zylinderachse zur Drehachse der Wippe parallel ist (siehe Abb.6). Das Gegendrehmoment des Zylinders dreht die Wippe geringfügig. Anhand dieser Drehung kann dieses Moment bestimmt werden. Mit der hier sichtbaren Anordnung wurden ca. 5·10-3 N·m gemessen.


Abb. 6 Abb. 7
Drehmoment und Gegendrehmoment
Mit dem Pendelkreisel kann sehr schön gezeigt werden, dass jedem Drehmoment ein dem Betrage nach gleiches Drehmoment entgegenwirkt. In der Abb.7 sehen wir den Pendelkreisel an einem Faden hängen. Beginnt die Drehung des Zylinders, dann dreht sich der obere Teil des Pendels mit entgegengesetztem Drehsinn. Dieses Experiment kann auch zur Demonstration des Drehimpulssatzes dienen.