Multifunktionen

Aus mehreren Funktionstermen wird eine Summe gebildet. Jeder Funktionsterm erhält eine Faktor st1(), welcher nach einem laufenden Zähler zwischen 0 und 1 wechselt. Immer dann, wenn er 1 anzeigt, wird derjenige Funktionsterm in einem Diagramm dargestellt, dessen st1() gleich 1 ist.

Definition der Funktion st1() : 0 < =j < 1 → st1(j) = 1, |j|>1 → st1(j) = 0. Im Fall st1(1) erhalten die Variablen x und d ihre Anfangswert.

1. Beispiel;

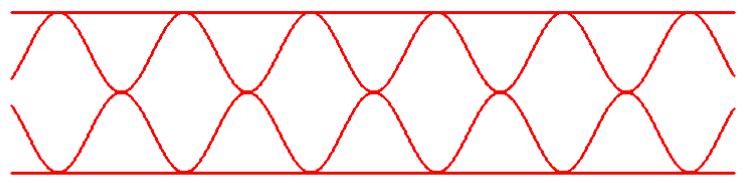
Mit der folgenden Zeile werden die Diagramm in der Abb. 1 erzeugt.

j=j+0,02; x=x+0,02; y=st1(j/18)*cos(x*2)+st1((j-18)/18)*(-cos(x*2)+2)+st1((j-36)/18)*3-st1((j-54)/18)*1;l=j

n=72, Anfangswert von x = -9

j= j+0,2 ist der Zähler. Zunächst wird cos(2*x) dargestellt, solange j<18 ist. Ist j =18, dann wird für cos(2*x) kein Diagrammpunkt mehr gesetzt, stattdessen werden x und d auf die Werte zurückgesetzt, die für sie im Variablenfeld stehen. -cos(2*x) + 2 kommt mit 0<=j <18 an die Reihe, darauf folgt die konstante Funktion y=3 mit 0<=j <36 usw. Wenn sich j, wie in dem hier vorgestellten Beispiel, zu jedem Funktionsterm um den gleichen Wert ändert, dann ist es angebracht die Programmzeile wie folgt zuschreiben:

j=j+0,02; x=x+0,02; y=st1(j/18)*cos(x*2)+st1(j/18-1)*(-cos(x*2)+2)+st1(j/18-2)*3-st1(j/18-3)*1;l=j

Achtung!

Zur Erprobung können die Programmzeilen mit Kopieren-Einfügen in das Programmfenster des Grafikrechners eingefügt werden.

Anmerkungen wie „n=72, Anfangswert von x = -9“ dürfen nicht mitgenommen werden.

Abb.1

2. Beispiel:

j=j+0,02; x=x+0,02;y=st1(j/19)*wrz(x)-st1(j/19-1)*wrz(x);l=j

n=38

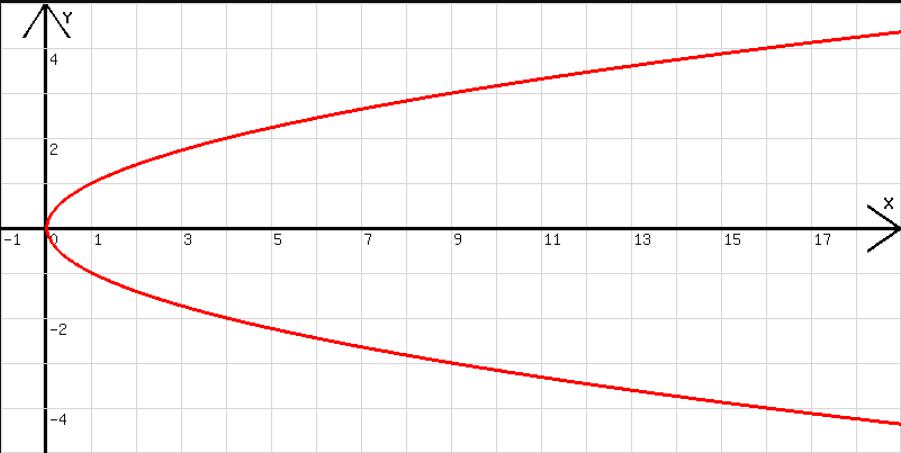
Abb.2

3.Beispiel:

j=j+1;x=st1(j/362)*9*cosg(d)+st1(j/362-1)*0,1*cosg(d)+st1((j-724)/14)*9*cosg(d*30)+st1((j-738)/8)*9*cosg(d*60);

y=st1(j/362)*9*sing(d)+st1(j/362-1)*0,1*sing(d)+st1((j-724)/14)*9*sing(d*30)+st1((j-738)/8)*9*sing(d*60);d=d+1;l=j;

n=746

Anmerkung: Während der Aufzeichnung des 6-Eck (60° ) ändert sich der Zähler j um 8. Mit st1((739-738) / 8) wird der Anfangspunkt gesetzt. Mit st1((745-738) / 8) wird der letzte Punkt des 6-Ecks gesetzt. Mit st1((746-738) / 8) erfolgt die Rückstellung von x und d auf deren Anfangswerte.

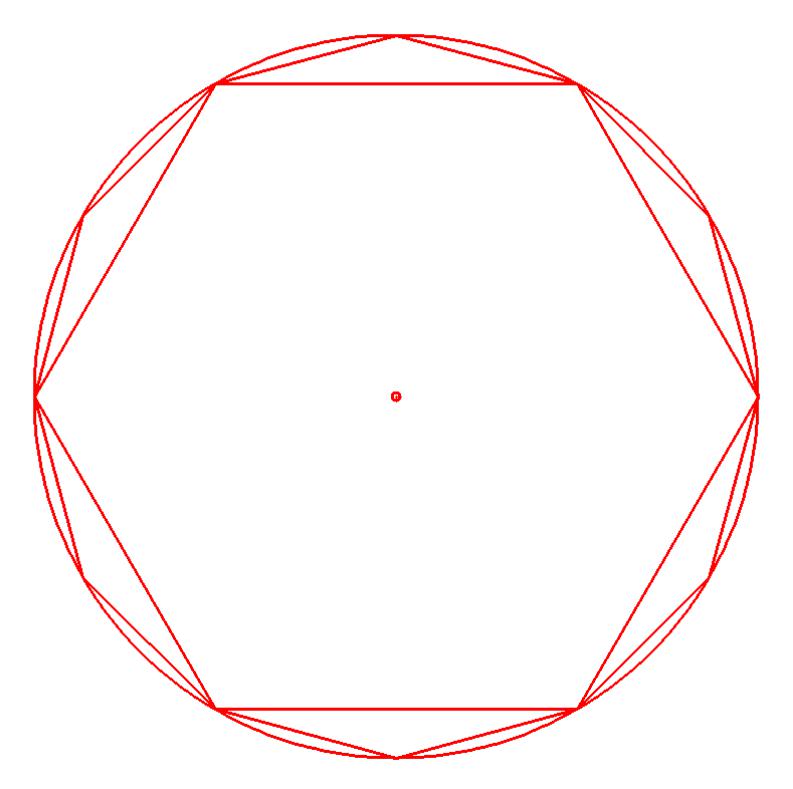
Abb.3

4. Beispiel:

j=j+1;x=st1(j/3)*(18*d-9)*cosg(60)+st1(j/3-1)*(18*d-9)*cosg(120)+st1(j/3-2)

*(18*d-9)*cosg(180); y=st1(j/3)*(18*d-9)*sing(60)+st1(j/3-1)*(18*d-9)*sing(120)+st1(j/3-2)*(18*d-9)*sing(180); d=d+1; l=j

n=9

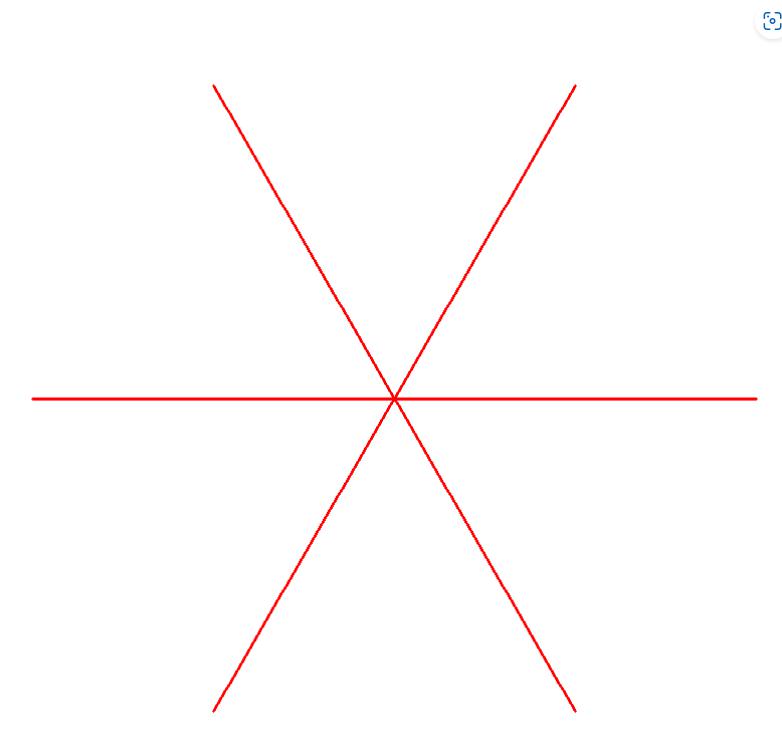
Abb. 4

5. Beispiel:

j=j+1;x=st1(j/362)*9*cosg(d)+st1(j/362-1)*0,1*cosg(d)+st1((j-724)/14)*9*cosg(d*30)+st1((j-738)/8)*9*cosg(d*60)+st1((j-746)/3)*(18*d-9)*cosg(60)+st1((j-746)/3-1)*(18*d-9)*cosg(120)+st1((j-746)/3-2)*(18*d-9)*cosg(180);

y=st1(j/362)*9*sing(d)+st1(j/362-1)*0,1*sing(d)+st1((j-724)/14)*9*sing(d*30)+st1((j-738)/8)*9*sing(d*60)+st1((j-746)/3)*(18*d-9)*sing(60)+st1((j-746)/3-1)*(18*d-9)*sing(120)+

st1((j-746)/3-2)*(18*d-9)*sing(180);d=d+1; l=j;

n=754

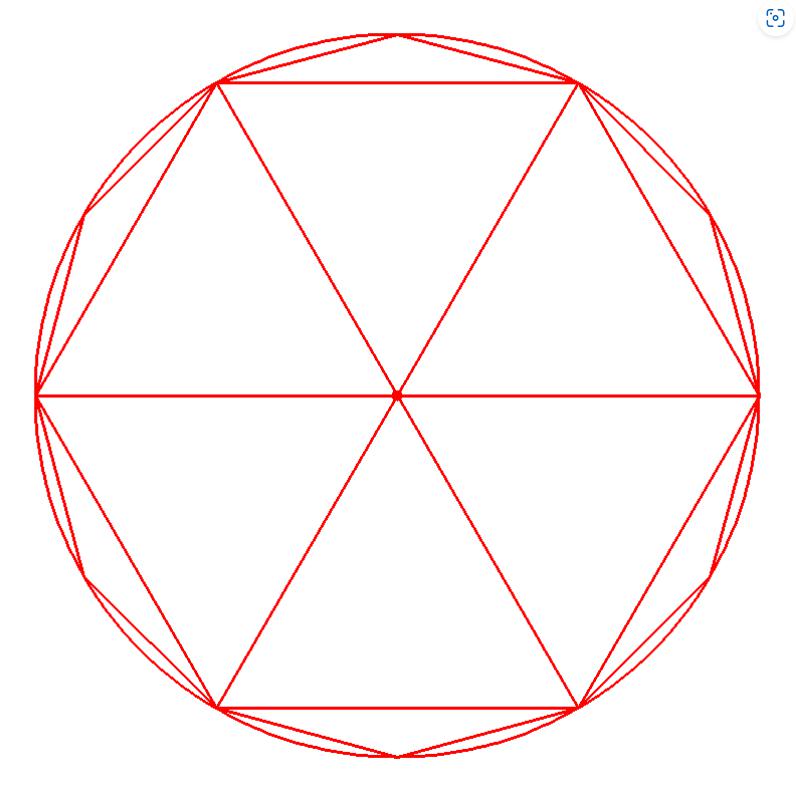
Abb.5