­-­

Berechnung von Sinus- und Kosinuswerten  mit Hilfe der Additionstheoreme

Mit Hilfe der Additionstheoreme  können die sin-  und  cos-Werte  für jeden beliebigen Winkel α berechnet werden. Man geht an diesen Winkel  in kleinen Schritten von beispielweise 0,1° vom Winkel 0,1° ausgehend heran. sin( 0,1°) kann gleich  dem zu   0,1° gehörenden Bogenmaß arc(0,1°) = 0,0017453283.. und   cos(0,1°) gleich 1 gesetzt werden. 

1. Schritt: Berechnung von sin(0,2°) = sin(0,1°+0,1°) und   cos(0,2°)= cos(0,1°+0,1°)

sin (0,2°) = sin(0,1° + 0,1°) =  sin(0,1°)  · cos(0,1°) +  sin(0,1°) ·cos(0,1°)

cos(0,2°) = cos(0,1° + 0,1°) = cos(0,1°) · cos(0,1°) - sin(0,1°) · sin(0,1°)

sin (0,2°) = sin(0,1° + 0,1°) = sin(0,1°)  · 1 + 0,0017453283 · cos(0,1°)

cos(0,2°) = cos(0,1° + 0,1°)  =  cos(0,1°) ·1  -  0,0017453283 · sin(0,1°)

2. Schritt: Berechnung von sin(0,3°) = sin(0,2°+0,1°) u. cos(0,3°) = cos(0,2°+ 0,1°)

sin (0,3°) = sin(0,2° + 0,1°) = sin(0,2°)  · cos(0,1°) + sin(0,1°) ·cos(0,2°)

cos(0,3°) = cos(0,2° + 0,1°) = cos(0,2°) · cos(0,1°) - sin(0,2°) · sin(0,1°)

sin (0,3°) = sin(0,2° + 0,1°) =  sin(0,2°)  · 1 + 0,0017453283  ·cos(0,2°)

cos(0,3°) = cos(0,2° + 0,1°) = cos(0,2°) · 1 - sin(0,2°) · 0,0017453283

Von sin(α) und cos (α) zu sin(α+0,1°) und cos(α+0,1°)

sin ( α +0,1°) =  sin(α)  · 1 + 0,0017453283  ·cos(α)

cos(α +0,1°)) = cos(α) · 1 - sin(α) · 0,0017453283

Programm zur Berechnung von sin - und cos -Werten

a = a+ 0,0017453283*b; b =b- a*0,0017453283; x=x+0,1; y=a; z=b

a (links) = sin ( α +0,1°) , a (rechts) = sin ( α , b(links) = cos ( α +0,1°) , b (rechts) = cos( α )

1 muss als Anfangswert von b eingetragen werden.

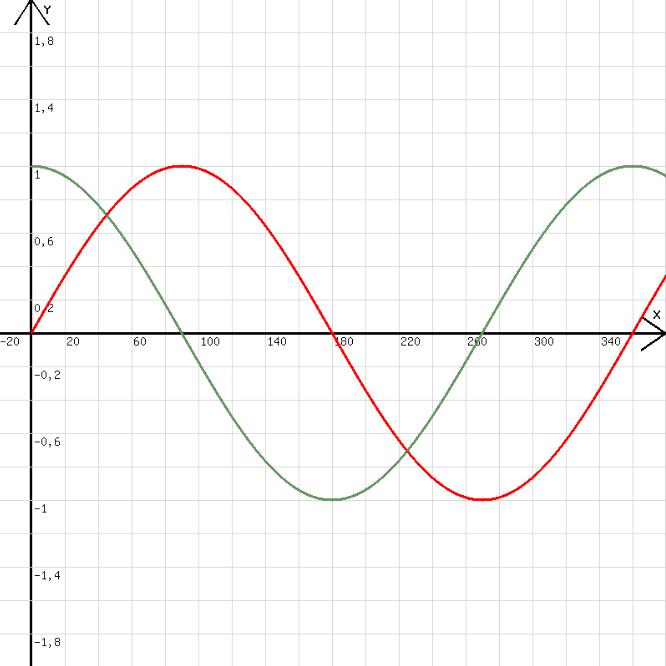
Mit diesem Programm werden die folgenden Diagramme erhalten.

Abb.1

Einstellungen zum Programm

Abb.2

Programm mit diesen Einstellungen