Berechnung von sin(x) und cos(x) mit Hilfe von Polynomen

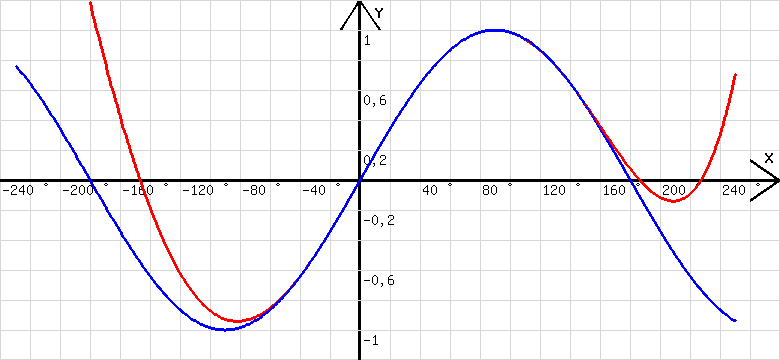
Mit dem Programm Bestimmung eines Polynoms n. Grades zu n+1 willkürlich gewählten Wertepaaren. kann ein Polynom online bestimmt werden, welches wie die Sinusfunktion y = sing(x) zu den Winkeln 0°, 30°, 45°, 60°, 90° und -30° die Werte 0; 0,5 ; 0,707 = 0,5· √(2); 0,866 = 0,5· √(3); 1; -0,5 liefert.

y= (0,017471111111111)*x+ (-5,5555555555569E-7)*x2+ (-9,0123456790124E-7)*x3+ (6,1728395061743E-10)*x4+ (8,2304526748962E-12)*x5

ist ein solches Polynom. Das rote Diagramm in der Abb.1 ist der zugehörige Graph. Das blaue Diagramm beschreibt die Sinusfunktion. Beide Diagramme wurden mit x=x+1;y=(0,017471111111111)*x^1+(-5,5555555555569E-7)*x^2+(-9,0123456790124E-7)*x^3+(6,1728395061743E-10)*x^4+ (8,2304526748962E-12)*x^5;w=sing(x);l=x­ und den in der Abb. 2 erkennbaren Einstellungen gezeichnet.

Es ist erkennbar, dass das Polynom zur Berechnung der Sinuswerte im Intervall [0°; 90°] geeignet ist. Mit diesen Sinuswerten können auch die Sinuswerte zu Winkeln außerhalb des genannten Intervalls bestimmt werden. Beispiele: sin(120°)= sin(60°), sin(200°) = -sin(20°)....

Abb.1


Abb.2



Wie in der Abb. 2  zu erkennen ist, weicht das Bogenmaß s/r=x bei sehr kleinen Winkeln nur wenig von yz/r , dem zugehörenden Sinus,  ab. y = x ist demnach zur Beschreibung von y=sin(x) geeignet, wenn man den Winkel im Bogenmaß angibt und sich auf sehr kleine Winkel beschränkt (siehe Abb. 3).

Abb. 2

Abb. 3
Mit der blauen Gerade ist y = x dargestellt.

Auf der Suche nach den Termen an· xn , die an das Bogenmaß x zur besseren Anpassung gehängt werden müssen, fragen wir uns, ob nicht besondere Eigenschaften von y = sin(x) als Hinweise dienen könnten.

 Es gilt: sin(-x) = -sin(x)

Für ein zur Beschreibung des Sinusfunktion geeignetes Polynom Ps(x) sollte deshalb gelten: Ps(-x) = -Ps(x)

Für Ps(x) kommen aus diesem Grund nur ungerade Exponenten in Frage.

Ps(x) = x + a3 · x3 + a5 · x5 + a7 · x7 ………;     x steht für Winkel im Bogenmaß 

Für die Kosinusfunktion gilt: cos(x) = cos(-x)

Somit kommen für das zu cos(x) passende Polynom Pc(x) aus diesem Grund nur gerade Exponenten in Frage.

Pc(x) = 1 + b2 · x2 + b4 · x4 + b6 · x6 ………;     x steht für Winkel im Bogenmaß

Zur Ermittlung der Werte a3 , a5 …., b2 , b4 …. nutzen wir folgende Eigenschaften von sin(x) und cos(x):

[sin(x)]2 + [cos(x)]2 = 1,      sin(2·x) = 2·sin(x)·cos(x)

↓

Ps(x)2 + Pc(x)2 = 1,     Ps(2·x) = 2·Ps(x) · Pc(x)

Ps(x)2 + Pc(x)2 = 1 + (1+2·b2) ·x2 + (2·a3 + 2·b4 + b22)·x4 …......

Nach Ps(x)2 + Pc(x)2 = 1 sind alle Faktoren vor x2, x4 …. gleich 0.

2·Ps(x) · Pc(x) = 2·x + [(a3 + b2)/4]·(2·x)3 + [(a5 +a3 ·b2 + b4)/16]·(2·x)5 …..... = Ps(2·x)

Nach Ps(x) = x + a3 · x3+ a5 · x5 + a7 · x7… gilt für Ps(2·x):

Ps(2·x) = (2·x) + a3 · (2·x)3 + a5 ·(2·x)5 ….....

↓

1+2·b2 = 0 (Faktor an  x2 in der Summe Ps(x)2 + Pc(x)2) →  b2 = - ½

[(a3 + b2)/4] = a3   →   a3 + b2 = 4·a3   →    a3 = - 1/6

2·a3 + 2·b4 + b22 = 0  →   b4 = - a3 - b22/2 = 1/6 -1/8 = 1/24

(a5 +a3 ·b2 + b4)/16 = a5   → a5 =1/120 

↓

sin(x) = x – (1/6)·x3 + (1/120) · x5 ….......

cos(x) = 1 - ½ · x2 + (1/24) · x4 …........... 

   6 = 2· 3 = 3!;   24 =1·2·3·4 = 4! ;    120 = 1·2·3·4·5 = 5!

Definition von n! (n Fakultät):       n! = 1 · 2 · 3 · 4 · 5…………………. · (n-1) · n

↓

sin(x) = x – x3/ 3! + x5/5! -  x7/ 7! + x9/9! - x11/11! + x13/13! – x15/ 15 !........ ( x: Winkel im Bogenmaß )

cos(x) = 1 – x2/ 2! + x4/4! – x6/ 6!…………….

Der in Abb. 4 sind die Graphen zu w = sin(x) und y= x-x^3/3!+x^5/5!-x^7/7! +x^9/9! - x^11/11! + x^13/13! - x^15/15! + x^17/17! - x^19/19! +x^21/21! zu sehen. Sie stimmen zwei Perioden lang hervorragend überein. Die Einstellung zur grafischen Darstellung sind in der Abb. 5 zu sehen.

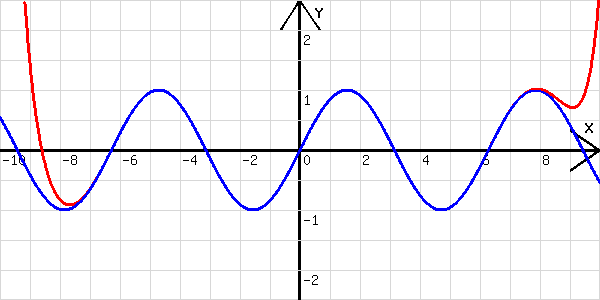
Abb.4 

 

Abb. 5