Darstellung der Exponentialfunktion y = ex durch ein Polynom

Herleitung eines Näherungspolynoms

Als Voraussetzung zur Herleitung eines  für eine Exponentialfunktion passenden Näherungspolynoms kann die für eine Exponentialfunktion gültige Regel      bx·bx = b(x + x)   dienen. Wir gehen davon aus, dass b so gewählt werden kann, dass in dem zu bx gehörenden Näherungspolynom   x1 = x den Beiwert 1 hat, und dass eine beliebig gute Annäherung an bx durch Anhängen weiterer Glieder a2 · x2 + a3 · x3 +a4 · x4 + a5 · x5 + ... erreicht werden kann.

bx = 1 + x + a2 · x2 + a3 · x3 .....

Die  Koeffizienten  des Polynoms  sind  durch  die  oben genannte Bedingung festgelegt.

bx · bx =  (1 + x + a2 · x2 + a3 · x3 ....) · (1 + x + a2 · x2 + a3 · x3 ....) =

1 + x + x  + a2 · x2  + x2  + a2 · x2 + a2· x3 + a2 · x3 + a3 · x3 + a3 · x3 ...... =

1 + (x + x) + (2·a2 + 1)/4 · (x + x)2 + (2·a3+2·a2)/8 · (x + x)3 ................

bx · bx = b(x + x) = 1 + (x + x) + (2·a2 + 1)/4 · (x + x)2 + (2·a3+2·a2)/8 · (x + x)3 ................

Nach den Voraussetzungen kann für b(x + x) auch geschrieben werden :

b(x + x)       =  1 + (x + x) +        a2       ·   (x + x)2 +        a3         ·   (x + x)3 .........

Ein Koeffizientenvergleich liefert:

(2 · a2 + 1)/4 = a2     →      a2 = ½

(2 · a3 + 2 · a2)/8 = (2 · a3 + 1)/8 = a3   →    a3 = 1/6

Bei einer Fortsetzung dieses Verfahrens findet man: a4 = 1/24,       a5 = 1/120 ......

Hierbei fällt auf : an = 1/n! ;   n! = 1 · 2 · 3 · 4 ........... · n    (Sprechweise: n Fakultät)

Beispiele: 4! = 1 · 2 · 3 · 4 = 24;       5! = 1 · 2 · 3 · 4 · 5 = 120

f(1) = 1 + 1/1! + 1/2! + 1/3! ................+1/n!   strebt mit wachsendem n gegen die Zahl   e = 2,718....

f(1) strebt gegen b1 =b, f(1) strebt gegen e.

↓

b = e

 f(x) = 1 + x + 1/2! · x2 + 1/3! · x3 ... beschreibt die Exponentialfunktion  y = ex.

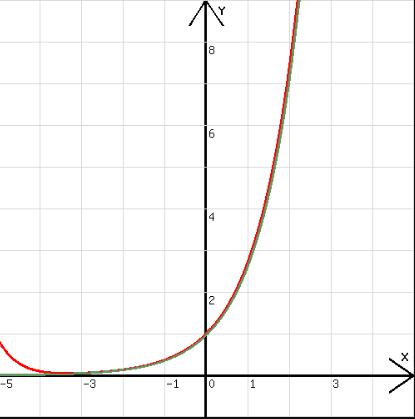
Mit x=x+0,01;y=1+x+1/2!*x^2+1/3!*x^3+1/4!*x^4+1/5!*x^5+1/6!*x^6+1/7!*x^7+1/8!*x^8+1/9!*x^9+1/10!*x^10;l=x ; z=exp(x-0.04)

enstehen die Diagramme in der Abb.1.

Abb.1

Der Polynomgraph passt gut auf den Graphen von y = ex !

Der Graph der Exponentialfunktion (grün) wurde um 0,04 nach rechts verschoben, damit der Graph zur Polynomfunktion (rot) auch noch zu sehen ist.



In der folgenden Abbildung (Abb. 2 ) sind die Einstellungen zur Aufnahme der Diagramme zu sehen.

Abb.2