Einführung der e-Funktion

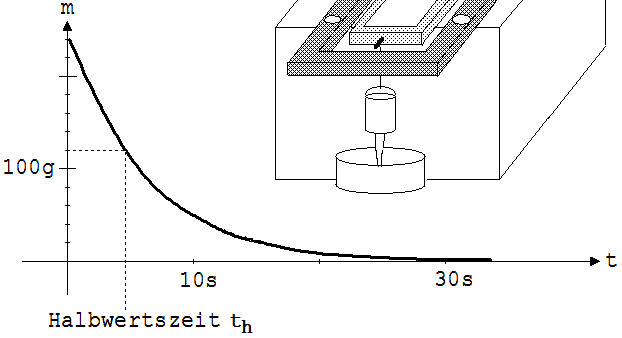
An der freien Schmalseite der Experimentierplatte hängt ein Gefäß mit textilem Boden. Aus diesem Gefäß läuft Wasser aus, wobei der Rechner das nebenstehende Diagramm aufzeichnet. Wie an dem Diagramm erkennbar, läuft in einer Zeit t_h, der sogenannten Halbwertszeit, unabhängig vom anfänglichen Wasserstand die Hälfte der Wassermenge aus.

Abb. 1

Im ersten Zeitabschnitt der Dauer t_h nimmt die Wassermasse m₀ auf m₀/2 ab. Am Ende des darauf folgenden Zeitabschnitts gleicher Dauer hat der Gefäßinhalt die Masse m = m₀·(1/2)·(1/2) und nach der Zeit t = n·t_h ( n = t/t_h ) gilt : m = m₀ · (1/2)ⁿ = m₀ · (1/2)^(t/th) = m₀ · 2 ^{- (t/th)}

Eine Exponentialfunktion beschreibt das Ausfließen des Wassers .

Die Fließgeschwindigkeit des Wassers wird durch die Reibungskraft begrenzt, welche der textile Boden dem Wasser entgegensetzt. Vermutlich ist diese Geschwindigkeit v der Reibungskraft F_R proportional.

Im Folgenden wird gezeigt, dass nach dieser Vermutung eine exponentielle Abnahme des Wasserstands zu erwarten ist.

Es gilt: m · g - F_R = m· a → F_R = m· a + m · g

m: Masse des im Gefäß befindlichen Wassers, a: Beschleunigung des Wassers, g: Erdbeschleunigung

F_R = m · g können wir schreiben, da die die Beschleunigung a des Wassers im Vergleich zu g vernachlässigbar klein ist. Δm (Δm <0) steht für die Änderung dieser Masse in einem kleinen Zeitabschnitt Δt. Sind z.B. 10g ausgeflossen dann gilt: Δm = Masse nach Δt – Masse vor Δt = - 10g . Sind z.B. 10g ausgeflossen dann gilt: Δm = Masse_{nach Δt} – Masse _{vor Δt} = - 10g . - Δm ist somit die Masse des Wassers, die in diesem kurzen Zeitabschnitt Δt ausfließt.

Aus der Annahme v ~ F_R folgt unter Berücksichtigung -Δm/Δt ~ v:

-Δm/Δt ~ F_R;   F_R = m· g   →   -Δ m ~ m· g·Δt   →    (- Δm / m )/Δt = Konstante = k

↓

Δm = m_{nach Δt} - m_{vor Δt} = - k · m_{vor Δt}· Δt    →    m _{nach Δt} = m_{vor Δt} - k·m _{vor Δt}·Δt

↓

m_{nach Δt} = m _{vor Δt}·(1- k·Δt )

Zur Simulation dieses Vorgangs wird in das Rechenfenster des hier vorhandenen folgende Zeile eingetragen:

t= t+h; m=m*(1-k*h); x=t;y=m;

Im Variablenfeld wird 0,01 (0,01 s ) für Δt = h , für k der Wert 0,2 (0,2 s^-1 ) und für den Anfangswert von m der Wert 100 (100g) eingetragen. Danach entsteht ein Diagramm, wie es in der Abb. 2 zu sehen ist.

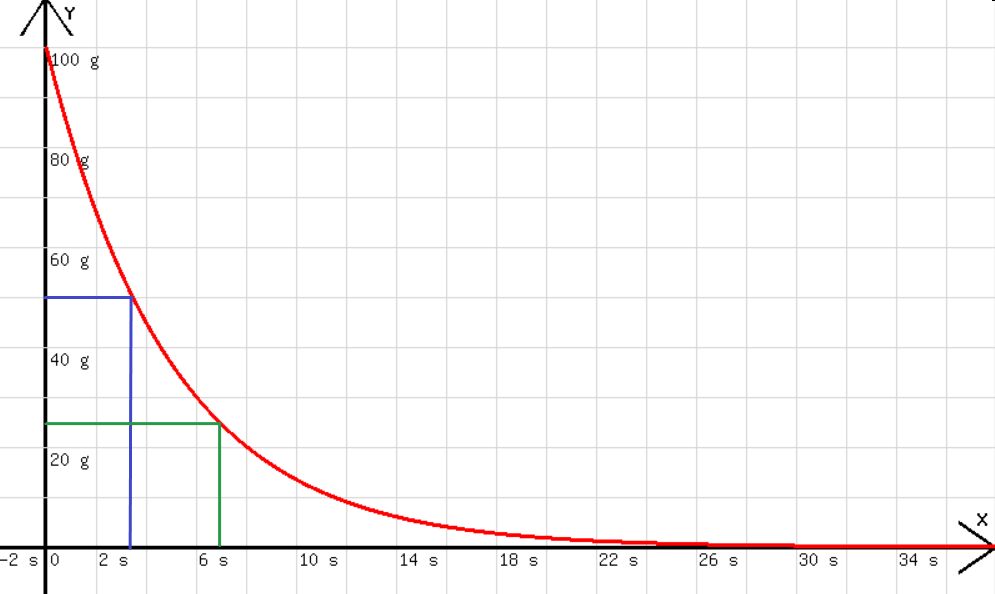
Abb. 2

Sehr deutlich ist zu erkennen, dass die Halbwertszeit unabhängig von der anfangs vorhandenen Wassermenge ist. Nach 3,4 s sind 50g ausgelaufen, nach weiteren 3,4 s sind nur noch 25 g im Gefäß. Die Behauptung F_R ~ v ist somit bestätigt.

Wie hängt die Halbwertszeit t_h von der Konstanten k ab ?

Mit größer werdendem k erfolgt die Entleerung schneller. Vermutlich sind t_h und k umgekehrt proportional. Erzeugt man das Diagramm mit verschiedenen Werten k , dann ist erkennbar, dass die Vermutung zutrifft. In jedem Fall ist das Produkt aus t_h und k gleich 0,692.

m = m₀·2 ^–t/th; t_h = 0,69 / k → m = m₀·2 ^{– (1/0,69) ·k·t} → m = m₀·[2 ^(1/0,69)] ^{– k·t}

Zur Vereinfachung dieses Terms wählen wir 2^1/0,69 =2,73 als Basis und benennen diese mit dem Buchstaben e. So können wir schreiben :

m = m₀ · e ^{– k·t}.

e als Grenzwert von [a/(a-1)]^a

Der oben angegebene Gleichung für die Entleerung soll nun hergeleitet werden.

m₁ = m₀ ·(1- k·Δt ) ist die Masse, die von der Anfangsmasse m₀ nach dem ersten Zeitabschnitt übrig ist. Für die Masse m₂ nach dem zweiten Zeitabschnitt gilt entsprechend: m₂ = m₁ ·(1- k·Δt ).

m₂ = m₁ ·(1- k·Δt );     m₁ = m₀ ·(1- k·Δt )    →    m₂ = m₀ ·(1- k·Δt )²

Die Masse m_n am Ende eines aus n Zeitabschnitten gebildeten Zeitraums der Größe t kann somit errechnet werden nach:

m_n = m₀·(1- Δt ·k)ⁿ = m₀·(1- Δt ·k)^{t/ Δt} = m_t ;    t/ Δt = n

Bei der Herleitung wurden sehr kleine Zeitabschnitt Δt vorausgesetzt, in denen sich die Änderung von m nicht nennenswert auf die Fließgeschwindigkeit auswirkt. Der durch die stetige Änderung der Fließgeschwindigkeit bedingte Fehler strebt mit kleiner werdendem Δt gegen 0. Da eine Gleichung der Form m_t = m₀ · e ^{– k·t} hergeleitet werden soll, wird m₀·(1- Δt ·k)^{t/ Δt} zu m₀·{(1-Δt ·k)^{- 1 / (k·Δt}} ^{- k·t} umgeformt. 1/( Δt ·k) nennen wir a.

m_t = m₀·{(1-1/a)^{- a}} ^{– k·t} = m₀·{[(a-1)/a]^{- a}} ^{– k·t} = m₀·{[(a/(a-1)]^a} ^{– k·t}

Wenn man y= [a/(a-1)] ^a in Abhängigkeit von x=a grafisch darstellt (siehe Abb. 3), dann ist erkennbar, dass y erwartungsgemäß mit zunehmendem x= a gegen einen Wert bei 2,73 strebt.

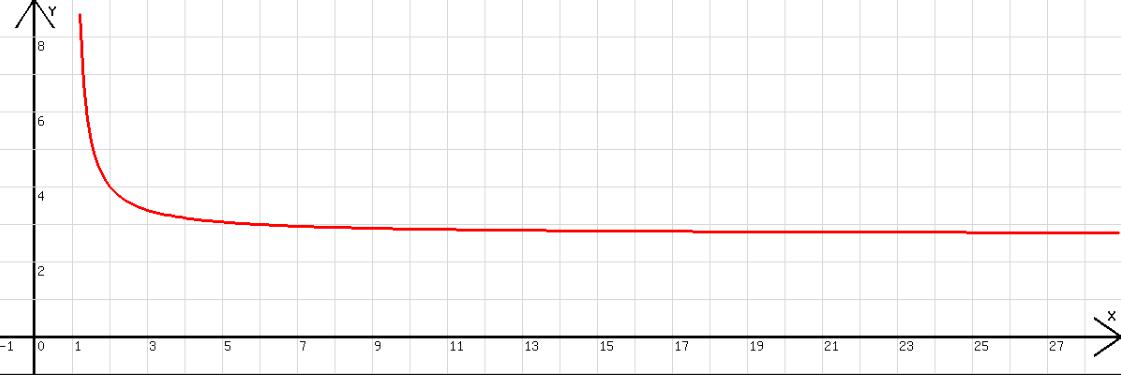
Abb. 3

Angesichts dieser Tatsache ist es sinnvoll, e als Grenzwert von [a/(a-1)]^a zu definieren.

e = lim [a/(a-1)]^a _{(a →∞)}

Unter der Voraussetzung a-1 = n gilt: [a/(a-1)]^a = [(n +1)/n]⁽ⁿ⁺¹⁾ = (1+1/n)ⁿ ·(1+1/n)

lim [a/(a-1)]^a (a →∞) = lim (1+1/n)ⁿ ·(1+1/n) (n →∞) = lim (1+1/n)ⁿ · lim (1+1/n) = lim (1+1/n)ⁿ · 1

lim [a/(a-1)]^a _{(a →∞)} = lim (1+1/n)ⁿ_{(n →∞)}

Hier ist noch Folgendes anzumerken:

(- Δm / m )/Δt = Konstante = k → Δm /Δt = k ·m

Unter Berücksichtigung von m = m₀ · e ^{– k·t} folgt: Δm /Δt = k · m₀ · e ^{– k·t}.

Wenn man es sehr genau nimmt, dann müsste das Gleichheitszeichen in der letzten Gleichung durch „≈“ ersetzt werden, denn dass Gleichheitszeichen ist nur für lim Δm /Δt ( Δt →0) = dm/dt erlaubt.

dm /dt = k · m₀ · e ^{– k·t}

Wir sehen: Den Differentialquotient einer Funktion A· e^b·t erhält man, indem man die Funktion mit b multipliziert. Die Ableitung von e^x (b=1) ist demnach gleich e^x.

Diese Regel kann leicht bewiesen werden.

e = lim (1+1/n)ⁿ = lim [1+1/(n/x)] ^n/x     →    e^x = lim {[1+1/(n/x)] ^n/x}^x = lim [1+1/(n/x)] ⁿ = lim [1+x/n] ⁿ

1+ x/n u

d uⁿ/dx = ( d uⁿ/du) · du/dx = n · u ^n-1 · (1/n) = [1+x/n] ^n-1 = [1+x/n] ⁿ /( 1+x/n)

lim ( 1+x/n) = 1.

↓

d lim[1+1/(n/x)] ⁿ / dx = lim [1+x/n] ⁿ

^↓

de^x/dx = e^x

Zum Programm

Einstellungen zum Programm t= t+h; m=m*(1-k*h); x=t;y=m;