Darstellung einer Zykloide

Was ist eine Zykloide ?

Der Leser erfährt es, wenn er diese Zeile anklickt.

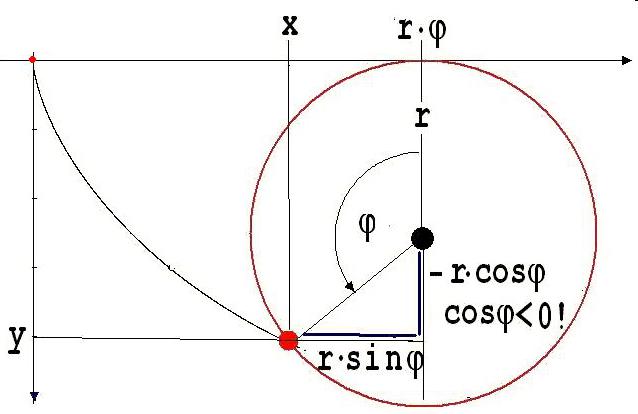
An der nachfolgenden Abbildung ist erkennbar, wie die Koordinaten x und y eines Zykloidenpunktes mit Hilfe des Drehwinkels berechnet werden.

Abb.1

x = r · ( φ - sin φ ), y = r · ( 1 - cos φ )

Zum Zeichnen einer Zykloide oberhalb der x-Achse werden die nachfolgenden Zeilen in das Programmfenster geschrieben.   In der Abb. 3 sind die Einstellungen zur Darstellung des Funktionsgraphen zu sehen.

d=d+0,1;r=1; x=r*(d-sin(d)); y=r*(1-cos(d)); l=x

Für φ wird die Variable d gewählt.

Abb.2

Abb.3

Anmerkung zur Zykloide:

Auf welcher Bahn rollt eine von einem Punkt P₁ zu einem seitwärts darunter liegenden Punkt P₂ am schnellsten ?

Der überaus geniale Mathematiker Leonhard Euler hat bewiesen, dass diese Bahn einer Zykloide entspricht.

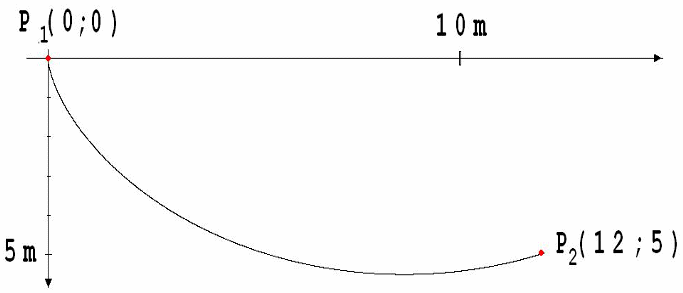
Abb.4