|
|
|
|
Abb. 1 |
Abb. 2 |
Über den Anstieg der Stromstärke I unter einer Batteriespannung UB in einer Spule mit der Induktivität L
Die hier skizzierte Versuchsanordnung zeigt zwei Leiterkreise mit gemeinsamer Spannungsquelle. Der regelbare Widerstand im Kreis 2 hat den gleichen ohmschen Widerstand R wie die Spule mit Eisenkern im Kreis 1. Wird der Schalter S geschlossen, dann erreicht das Glühbirnchen im Kreis 1 seine volle Lichtstärke später als das im Kreis 2, welches sofort in voller Stärke strahlt. Der gebremste Stromanstieg im Kreis 1 ist im Diagramm der Abb. 2 dargestellt.
|
|
|
|
Abb. 1 |
Abb. 2 |
Erklärung:
Das in der Spule entstehende Magnetfeld induziert im Kreis 1 eine Induktionsspannung Uind, die nach der Lenzschen Regel dem Anwachsen des elektrischen Stromes entgegenwirkt. Die volle Stärke Im = UB / R ist im Kreis 1 erst dann erreicht, wenn das Magnetfeld aufgebaut ist.
Für die im Kreis 1 induzierte Spannung gilt:
Uind ~ dΦ/ dt; Φ ~ I → dΦ/dt ~ dI/dt → Uind ~ dI/dt → Uind / (dI/dt) = Kontante
Nach der Lenzschen Regel handelt es sich um eine negative Konstante, denn Uind wirkt der Stromänderung entgegen. Der Gegenwert dieser Konstanten heißt Induktivität L.
- Uind / (dI/dt) = L → Uind = - L · dI/dt
Die Einheit V·s/A wird Henry (Abkürzung: H) genannt.
Wie ändert sich der Strom nach dem Einschalten ?
Der Stromänderung während eines kleinen Zeitabschnitts wird durch die folgenden Gleichung beschrieben:
I · R - UB = Uind , Uind = - L · ΔI/Δt → I · R - UB = = - L · ΔI/Δt → ΔI = ( UB – I · R) · Δt / L
UB = konstante Batteriespannung, R = ohmscher Widerstand im Leiterkreis (Glühbirne, Spule, innerer Widerstand der Batterie)
Wichtige Anmerkung: Die Induktionsspannung ist eine Wirbelspannung, Sie steht für die Arbeit, die das elektrische Feld verrichtet, wenn 1 Coulomb in kleinen Portionen links herum durch die Schleife geführt wird.
Hat die Stromstärke ihren Maximalwert Im erreicht ( ΔI = 0), dann gilt: UB = ( Im · R )
Für die Stromstärke nach dem Zeitabschnitt Δt gilt demnach:
Inach - Ivor = (UB – I· R)·Δt / L → Inach = Ivor + (UB – I· R) · Δt / L ( I = Ivor)
Mit dem nachfolgenden Programm wird die Stromstärke in Abhängigkeit von der Zeit unter der Bedingung (L=1H, R =10 Ohm, UB = 9V, Δt = h =0,001 s) dargestellt.
I = I + ( U - I *R)* h / L ; t = t + h; y = I; x = t
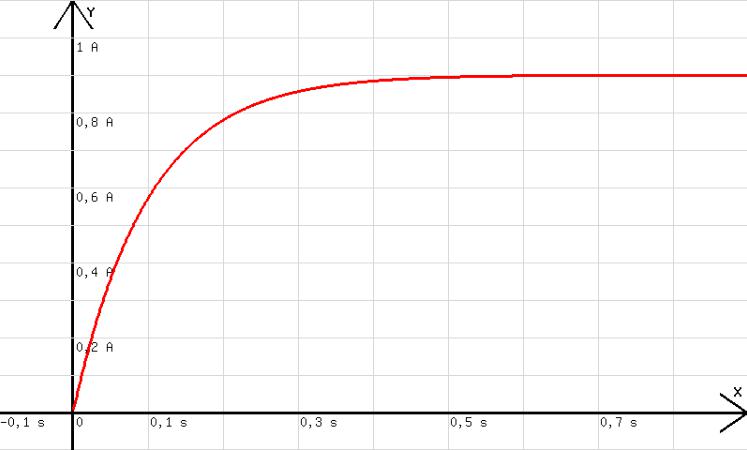
Abb.3