Schwingungen

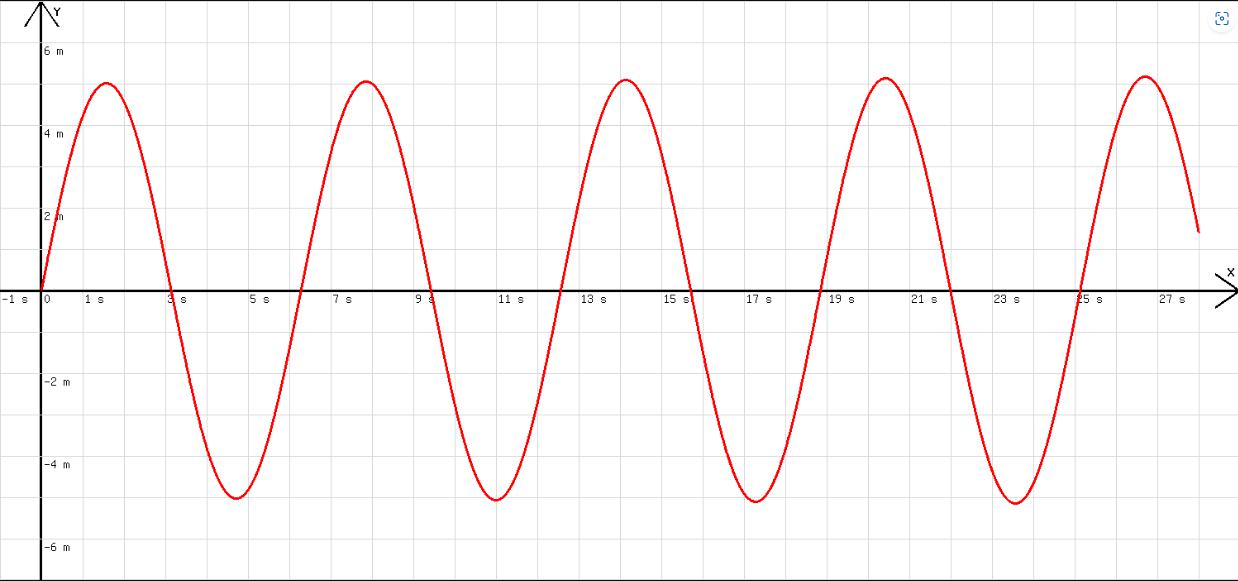
Ein an einer Spiralfeder schwingender Gegenstand mit der Masse m = 1 kg bewege sich mit der Geschwindigkeit 5m/s zum Zeitpunkt t=0 durch den Schwingungsmittelpunkt. Ein Weg-Zeit-Diagramm (y-t-Diagramm) des schwingenden Gegenstands (siehe Abb. 1) für den Fall k=Federkonstante=1kg/s² kann in folgendem Programm realisiert werden: k=1;m=1;f = -k*y; a=f/m; h=0,005; x=x+h; y=0,5*a*h^2+c*h+y; c=c+a*h; l=x;. In das Variablenfeld werden für c (Anfangswert) und n die Werte 5 und 28 eingetragen.

Abb.1

Anmerkung zu dem Programm:

Die Bewegungszeit wird in sehr kleine Zeitabschnitte Δt = h zerlegt. Ein Δt ist so klein, dass innerhalb dieses Δt = h die Kraft nach Richtung und Betrag als konstant angesehen werden kann. Mit den für konstante Kräfte geltenden Bewegungsgleichungen wird die Änderung des Orts und der Geschwindigkeit während des ersten Zeitabschnitts Δt berechnet.

a = F /m ; F : Kraft während des Zeitabschnitts Δt ; a: Beschleunigung

y_n = 0,5 ·a · Δt²+ v_v ·Δt + y_v , v_n= a· Δt + v_v entspricht: y = 0,5 * a * h^2 + c * h + y; c = c + a * h;

Die Größen mit dem Index n sind solche nach Δt, die mit dem Index v sind solche vor Δt.

Nach dieser Rechnung ist der Ort und die Geschwindigkeit zu Beginn des zweiten Abschnitts Δt bekannt. Mit deren Werten wird daraufhin der Ort und die Geschwindigkeit zu Beginn des dritten Abschnitts ( nach dem Ende des 2. Abschnitts) berechnet usw..

Geht man davon aus, dass der schwingende Körper eine der Geschwindigkeit proportionale Reibungskraft erfährt, dann muss für die Kraft geschrieben werden: f= -k*y -j*c .

k=1;m=1; f= -k*y -j*c; a=f/m; h=0,005; x=x+h; y=0,5*a*h^2+c*h+y; c=c+a*h; l=x;

Mit j=0,2 wird das Diagramm in der Abb. 2 erhalten.

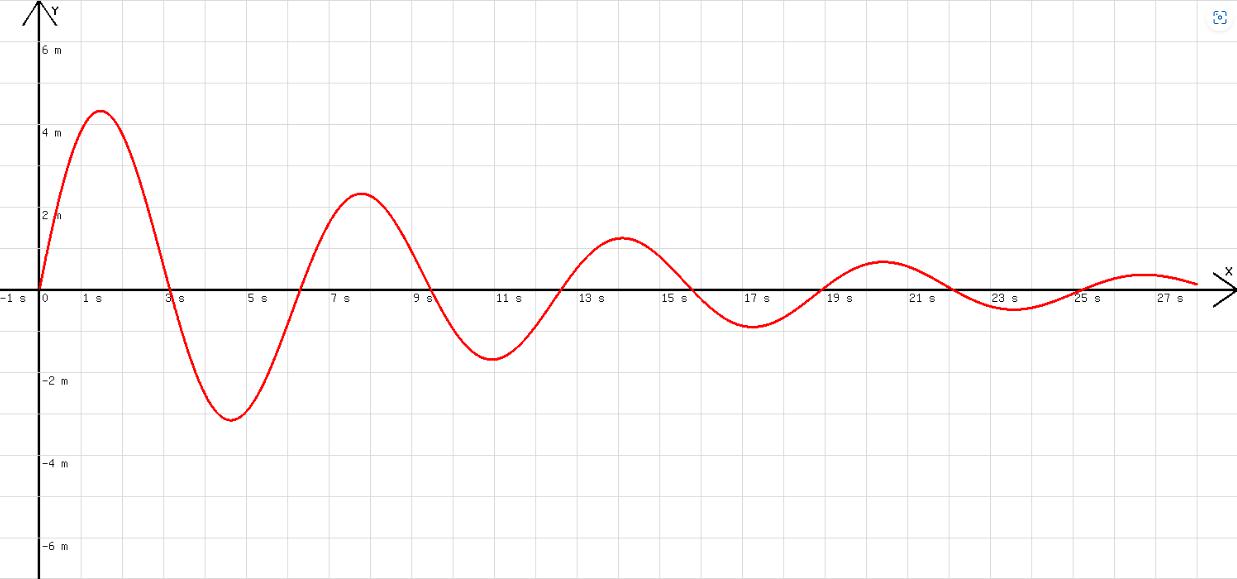
Abb.2

Mit k=1;m=1;f = -k*y +0,5*sin(x); a=f/m; h=0,005; x=x+h; y=0,5*a*h^2+c*h+y; c=c+a*h; z=0,5*sin(x); l=x; wird eine Schwingung simuliert, die von einer Kraft F= 0,5*sin(x) (Resonanzfall) erzwungen wird. In diesem Fall muss die Anfangsgeschwindigkeit c gleich 0 gesetzt werden. Nach den ersten Schwingungen ist ein linearer Anstieg der Amplitude erkennbar (siehe Abb.3). Das grüne Diagramm zeigt die Kraft F= z= 0,5*sin(x) an.

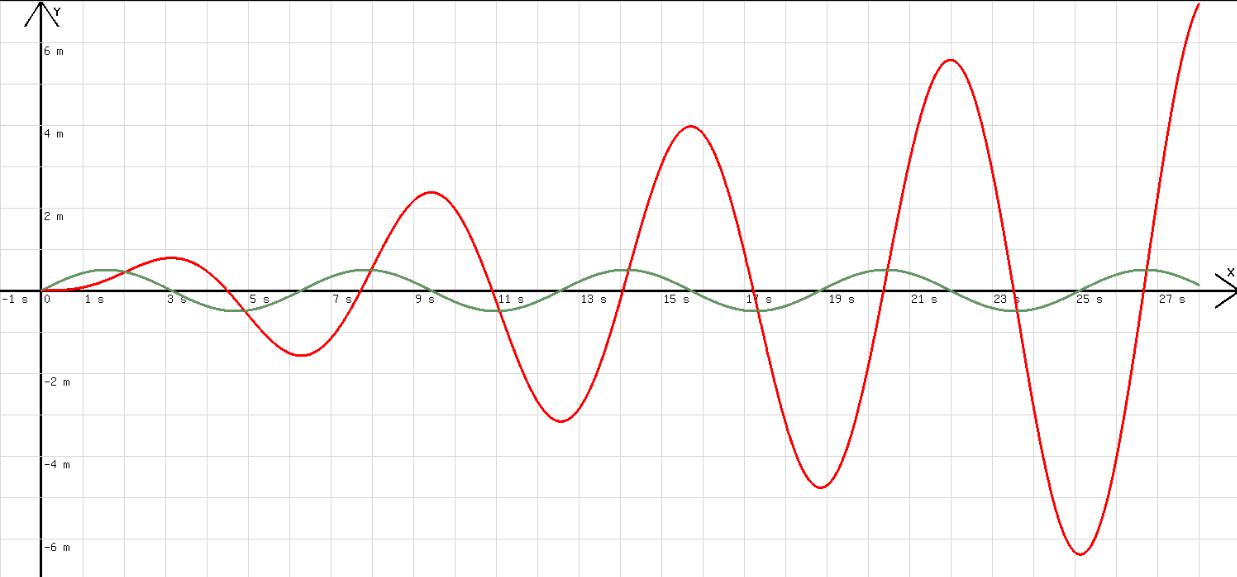
Abb.3

Einstellungen zum Programm

Abb.4

Weicht die Erregerfrequenz von der Eigenfrequenz des Federpendels ab, dann erhält man im ungedämpften Fall ein Schwingungsdiagramm mit periodisch schwankender Amplitude. Das Diagramm in der Abb. 5 wurde mit dem 0,8-fachen der Eigenfrequenz erhalten

Abb.5

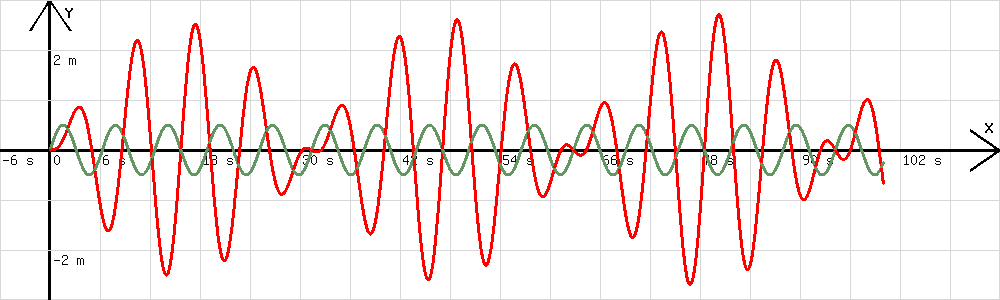
Zum Programm