Zur Bewegung eines Planeten um die Sonne

Für die Beschleunigung eines Planeten unter der Anziehungskraft der Sonne gilt: a_x = - (G·M/r³)·x, a_y = - (G·M/r³)·y. G ist die Gravitationskonstante, M ist die Masse der Sonne und r ist der Abstand des Planeten von der Sonne. Die folgende Programmzeilen sind für eine Bewegung nach diesen Beschleunigungsgesetzen geschrieben.

K=1,334E+20; h=778,35; r=wrz(x^2+y^2); a=-k/r^3*x; b=-k/r^3*y; a=0,5*j*(a-o)+a;b=0,5*j*(b-p)+b; x=0,5*a*h^2+c*h+x; y=0,5*b*h^2+d*h+y ; c=c+a*h; d=d+b*h; o=a;p=b; l=l+1; j=1; t=t+h; w=(r+wrz(y^2+(x+8,3E10)^2))/2; u=x; v =(y*c-x*d)*0,5*1E-5;

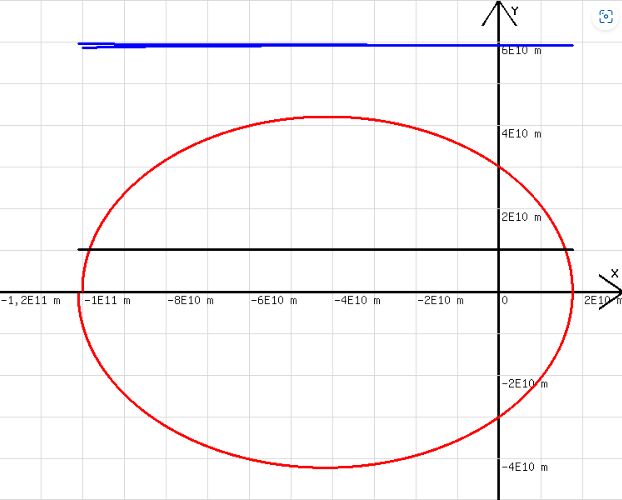
k Steht für G·M. Als Startpunkt wird der Punkt (-1E11m , 0) und als Startgeschwindigkeit v_y = d = 20000 m/s festgelegt. w ist die halbe Summe aus den Abständen der Bahnpunkte von den beiden Brennpunkten B1 und B2. Sie wird von dem waagrechten blauen Diagramm angezeigt. Sie erweist sich als konstant. Die Bahn (siehe Abb. 6) ist somit eine Ellipse mit den Brennpunkten B1 und B2. Ebenfalls konstant ist die Flächengeschwindigkeit v =(y*c-x*d)*0,5. v/(1E5 m²/s) wird von dem schwarzen Diagramm angezeigt. Mit dieser Darstellung erfahren die beiden ersten Keplerschen Gesetze eine Bestätigung.

Abb.1

Zum Programm

Einstellungen für das Programm

Abb.2