Berechnung von Strömen in einem Leiternetz

Aufgabe:

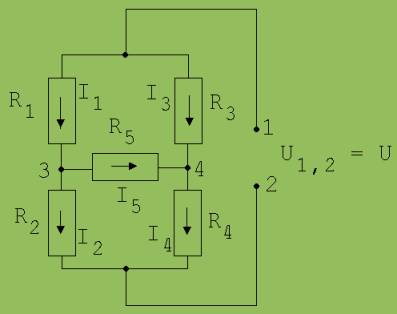
Die Ströme in dem in Abb. 1 skizzierten Netzwerk sollen berechnet werden. Die Pfeile zeigen die Richtungen an, für welche die Ströme positiv zu zählen sind.

Abb. 1

Die Grundlage zur Berechnung derartiger Leiternetze bilden die beiden Kirchhoffschen Gesetze:

1. Kirchhoffscher Satz

Die Summe der zu einem Knoten (Verzweigungspunkt) hin fließenden Ströme ist gleich der Summe der abfließenden Ströme (siehe Abb.2).

Beispiel:

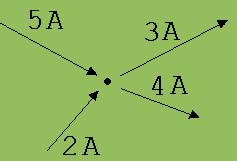5 A + 2 A = 3 A + 4 A

Abb. 2

Meistens kann man zunächst keine Entscheidung über die Stromrichtung treffen. In einem solchen Fall werden willkürlich Richtungen festgelegt, für welche die Ströme positiv zu zählen sind (siehe Ab. 3). Nach dieser Vereinbarung gilt auch:

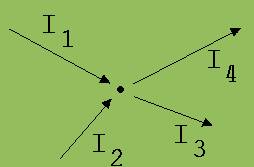I₁ + I₂ = I₃ + I₄

Abb. 3

Beispiel:

I₁ = 5 A ;   I₂ = -3 A;   I₃ = -4 A;   I₄ = 6 A

I₁ und I₃ fließen zum Knoten hin, I₂ und I₄ fließen vom Knoten weg.

5 A + (-3 A) = - 4 A + 6 A

5 A + 4 A = 6 A + 3 A

2. Kirchhoffscher Satz

Entlang eines geschlossenen Weges ( Leitermasche) ist bei Abwesenheit magnetischer Wechselfelder die Summe aller Spannungen gleich 0.

Beispiel:

Wir durchlaufen die Masche links herum bei + beginnend.

U – I₂ · R₂ + I₃ · R₃ – I₄ · R₄ + I₁ · R₁ = 0

Diese Gleichung gilt auch dann, wenn die Pfeile nicht die wahren Stromrichtungen anzeigen.

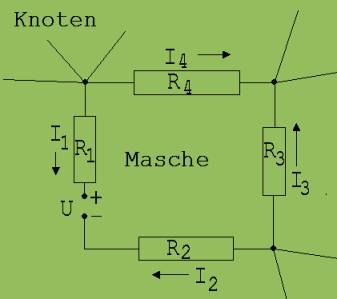
Abb. 4

Im Folgenden sind die zu dem in Abb. 1 dargestellten Netzwerk passende Maschen – und Knotengleichungen zu sehen:

 Masche in der Abb. 1 vom Punkt  1 durch R₁ und R₂  zum Punk 2 und von dort zum  Punkt 1: R₁ ·  I₁  + R₂ · I₂ =U

 Masche in der Abb. 1 vom Punkt  1 durch R₃ und R₄  zum Punk 2 und von dort zum  Punkt 1: R₃ · I₃ + R₄ · I₄ = U

 Masche in der Abb. 1 mit den Widerständen R₁ , R₅ und R₃ :  R₁ · I₁ + R₅ · I₅ – R₃ · I₃ = 0

Knotengleichungen zum Knoten 3 in der Abb. 1: I₁ – I₅  - I₂ = 0 

Knotengleichungen zum Knoten 4 in der Abb. 1: I₃ + I₅ – I₄ = 0

Beispiel: R₁ = 10 Ω ; R₂ = 5 Ω ; R₃ = 15 Ω ; R₄ = 8 Ω; R₅ = 20 Ω; U = 10 V

Anhand dieser Angaben ist das folgende Gleichungssystem aufzustellen:

Nach Wahl des Programms zur Lösung linearer Gleichungen (es handelt sich hier um 5 Gleichungen) werden die Widerstandswerte in die für lineare Gleichungen vorgesehene Felder eingetragen .   I₁, I₂, I₃, I₄ und I₅ werden den Variablen x(1), x(2), x(3), x(4) und x(5) zugeordnet. Nach dem Eintrag aller Gleichungen mit den Nummern 1 – 5 wird   „Start“ angeklickt.