Bestimmung einer Wurzel durch Iteration
Aufgabenstellung:
Es soll die Lösung von y² = x ( z. B. x = 41) bestimmt werden.
x = y² ↔ x= y · y ↔ x/y = y
y1 sei eine etwas ungenaue, geschätzte Lösung.
Der wahre Wert y ( Lösung von x = y² ) liegt zwischen x/y1 und y1
Begründung:
Ist y1 < y dann gilt: x/y1 > y
Mit kleiner werdendem Nenner wird der Quotient größer.
Der Mittelwert y2 von x/y1 und y1 liegt dem Wert y näher.
y2 = (y1 + x/y1) /2
Noch besser passt y3 = (y2+ x/y2)/2 und dann y4 = (y3+ x/y3)/2.
Diese schrittweise Annäherung an die richtige Lösung mit y1, y2, y3, y4 usw. heißt Iteration (Iter: lateinisch der Schritt).
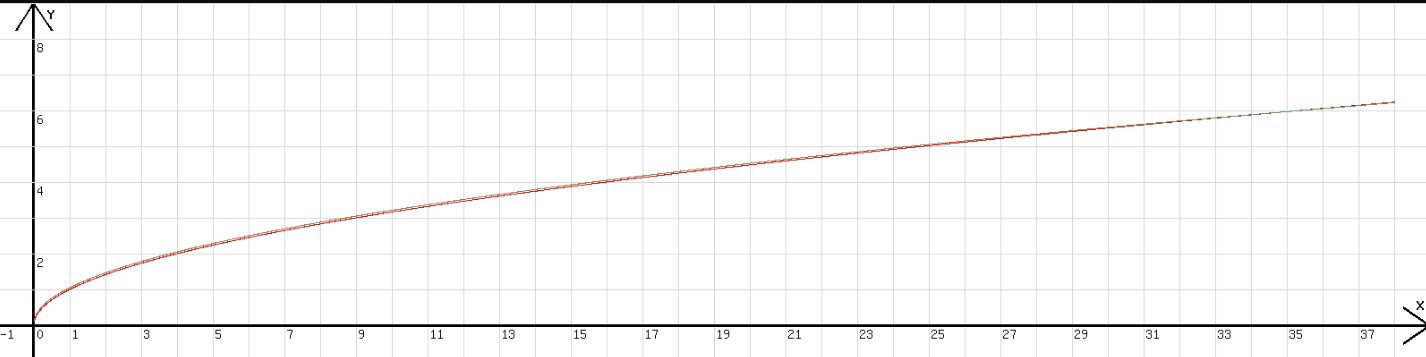
Mit dem Nachfolgenden Programm wird wird das durch Iteration gewonnene y in Abhängigkeit von x dargestellt (rotes Diagramm). Das an dieses Programm angehängte z=wrz(x)+0,05 soll die Genauigkeit der Iteration zeigen. wrz(x) steht für √(x). Die durch Iteration gewonnene Kurve wird von dem Grafen zu z=wrz(x) abgedeckt.
x=x+0,01; y=1; y=0.5*(x/y+y);y=0.5*(x/y+y);y=0.5*(x/y+y);y=0.5*(x/y+y); z=wrz(x)+0,05; l=x
