Fallbewegung in einer Flüssigkeit

Wir stellen uns eine in Öl fallende Eisenkugel vor (Fallbeginn zum Zeitpunkt t = 0). Der Gewichtskraft m · g wirkt eine der Geschwindigkeit proportionale Reibungskraft F_R = k ·v entgegen.. Die Geschwindigkeit wächst solange bis die Gewichtskraft gleich der Reibungskraft ist.

Wie ändert sich die Geschwindigkeit v mit der Zeit ?

F_R /v = k (Konstante)   →   F_R = k·v 

Für die Beschleunigung a gilt demnach:   m· a = m· g – k · v    →    a = g – k· v/m

Wenn k· v/m den Wert g erreicht, dann verläuft die Bewegung gleichförmig mit der Geschwindigkeit v = g· m/k. In einem Zeitabschnitt Δt =h nimmt die Geschwindigkeit v um a·h zu. Für das v_{nach h} gilt: v_{nach h} = v_{vor h} +a · h. Für den Weg w nach h gilt somit: w_{nach h} = w_{vor h} + v· h

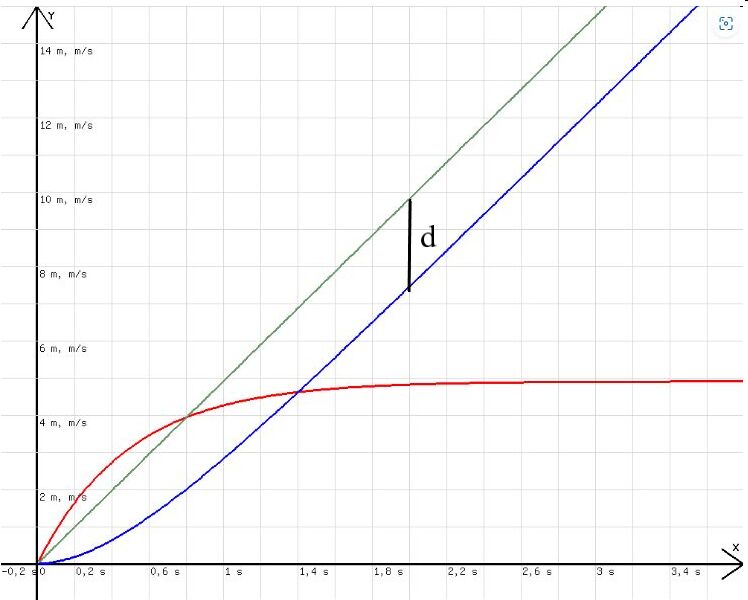
Die Diagramme in der Abb. 1 zeigen die Geschwindigkeit der Kugel und deren Weg in Abhängigkeit von der Zeit. Sie­ wurden mit dem folgenden Programm erhalten:

k=2; m=1; h=0,01; a=9,81-k/m*c; c=c+a*h; x=x+h; y=c; w=c*h+w; z= m*9,81/k*x; l=x;

c und y stehen für v , w steht für die zurückgelegte Strecke s und x steht für t !

Mit z= m*9,81/k*x; wird ein Weg-Zeit-Diagramm (grün) für eine Bewegung mit konstanter Geschwindigkeit v=g·m/k dargestellt.

Abb.1                                                                                  Abb.2

Das rote Diagramm ist das v-t-Diagramm (y-t-Diagramm), das blaue das zugehörende s-t-Diagramm (w-t-Diagramm). Hätte die Bewegung mit der Endgeschwindigkeit v = g· m/k begonnen, dann wäre sie gleichförmig nach dem grünen Diagramm (z-t-Diagramm) verlaufen.

Das Verhältnis v/ v_Ende = v·k /(m· g) ist ein Wert f der nach dem Beginn der Bewegung von 0 auf 1 ansteigt. Für die Geschwindigkeit v kann  v = m·g / k ·f  geschrieben werden.  Der Term (1 - e ^{– j ·t} ) mit einer noch unbekannten Konstanten j  kommt als Faktor f in Frage. Je größer j ist, desto schneller wird die Endgeschwindigkeit erreicht. Es ist davon auszugehen, dass eine große Reibungskraft und eine geringe Gewichtskraft in kurzer Zeit zur Endgeschwindigkeit führen.

Vermutung: j = k/m    →  v = m · g/k · (1- e^{- (k/m) · t})

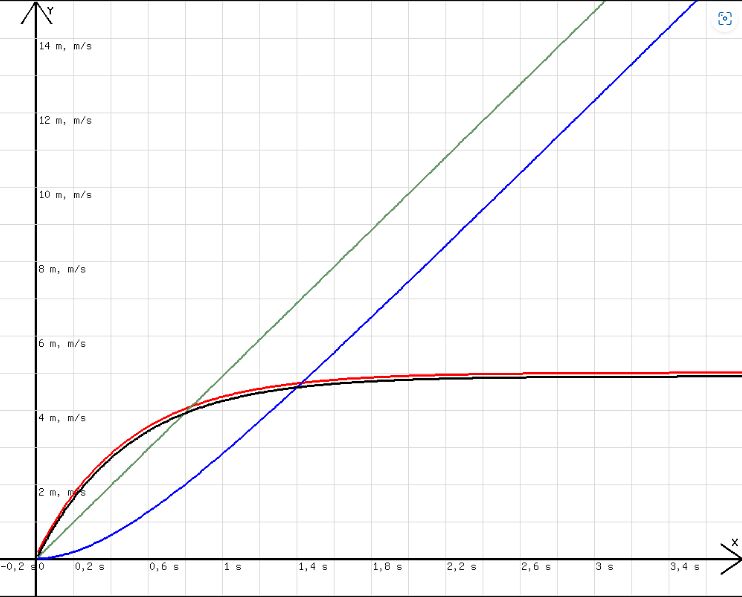
Mit der folgenden Zeile wird diese Vermutung bestätigt. Die Diagramme zu y(Geschwindigkeit) und v(Geschwindigkeit) stimmen überein. In der Programmzeile wurde zu c der Wert 0,1 addiert, damit das y-Diagramm neben dem v-Diagramm sichtbar wird.

k=2; m=1; h=0,01; a=9,81-k/m*c; c=c+a*h; x=x+h; y=c+0,1; w=c*h+w; z= m*9,81/k*x; v=m*9,81/k*(1-exp(-k/m*x)); u=x; l=x;

Hätte der Körper schon zu Anfang  die Höchstgeschwindigkeit m ·g/k,  dann würde für den zurückgelegten Weg s gelten: s = m · (g/k) ·t . Für s gilt jedoch  s < m·(g/k)·t. Die mit der senkrechten Strecke in der bei 2 Sekunden in der Abb. 1 angedeutete Differenz d zwischen m·(g/k)·t und dem wahren Weg s wird sich vermutlich nach dem Bewegungsbeginn ähnlich wie die Geschwindigkeit zu einem Maximalwert entwickeln .

Vermutung : d = m · (g/ k) · t – s = r · (1 - e ^{– k · t/m} )

Der unbekannte Faktor r  muss  von m, g und k abhängen und die Einheit eines Weges haben. Vermutlich ist  r = m² / k² · g , denn m²/k² · g  hat die Einheit eines Weges.

↓

  s = m · g/ k · t -  m² / k² · g ·  (1 - e ^{– k · t/m} )

Zur Prüfung dieser Annahme wird das Grafikprogramm mit „k=2; m=1; h=0,01; a=9,81-k/m*c; c=c+a*h; x=x+h; y=c; w=c*h+w; z=m*9,81/k*x; u=x; v=m*9,81/k*x-m^2/k^2*9,81*(1-exp(-k*x/m))+0,15; l=x;“  gestartet. Dabei wird das ursprüngliche, blaue Weg-Zeit-Diagramm überzeichnet. Dem s der letzten Gleichung entspricht das v in der Programmzeile. In der Programmzeile wurde zu v(Weg) der Wert 0,15 addiert, damit das w-Diagramm(blau) neben dem v-Diagramm (schwarz) sichtbar wird.

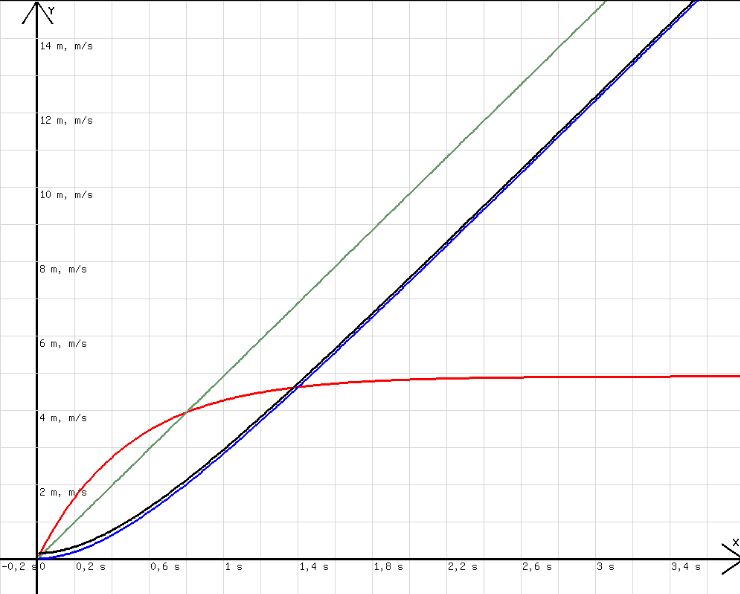
Abb. 3

Einstellungen zum Programmablauf

Abb.4