Ellipse, Hyperbel

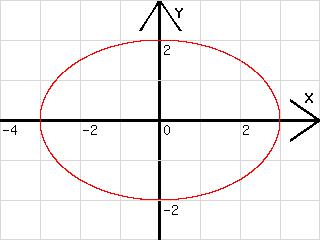
Mit d=d+0,01; x=3*cos(d); y=2*sin(d); l=d wurde die Ellipse in der Abb.1 aufgenommen.

Aus x=3*cos(d);    y=2*sin(d);   folgt:   x/3 =cos(d),   y/2 = sin(d)   →   x² / 9  +  y² /4 = 1    (sin(d)² + cos(d)² = 1 !)

Abb. 1

Mit d=d+0,01; x=2*cosh(d); y=3*sinh(d); u=-2*cosh(d); v=3*sinh(d) wurde die Hyperbel in der Abb. 2 gezeichnet.

Für d wurde als Anfangswert -4 eingetragen.

sinh(d) = (e^x – e^-x)/2,    cosh(d) = (e^x + e^-x)/2 ,

cosh(d) = x/2,   sinh(d) = y/3

 cosh(d)² - sinh(d)²  =  1    →    x² / 4 - y² /9 = 1

Hiermit wird die Namensgebung „Sinus-hyperbolicus und Kosinus-hyperbolicus” für sinh und cosh verständlich.

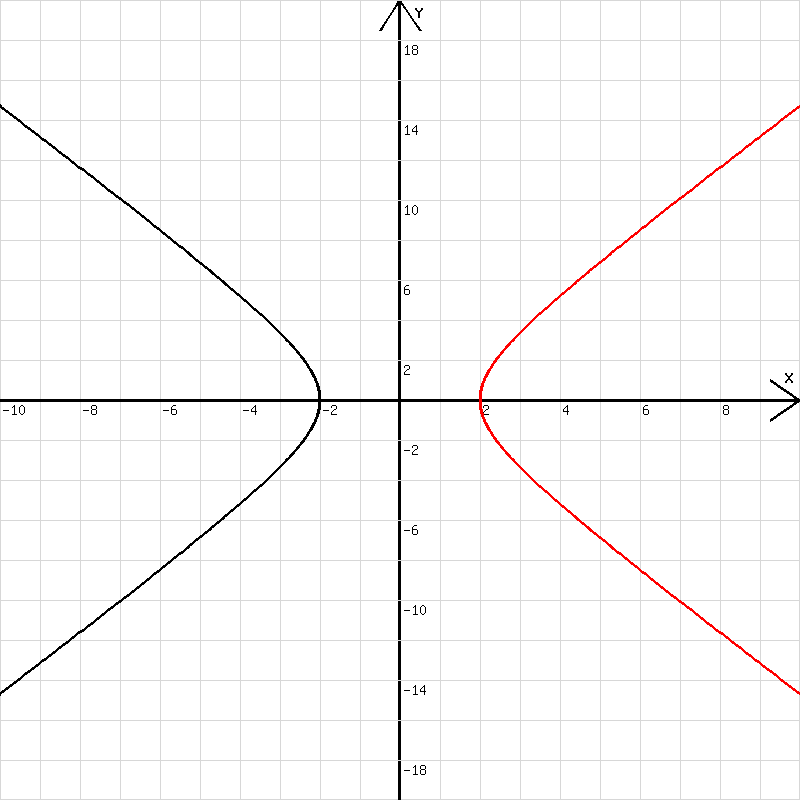
Abb.2