Elektrische Schwingungen

Der Schwingkreis

Wird der am U-Rohr sichtbare Hahn geöffnet, dann schwingt das Wasser zwischen den beiden Schenkeln hin und her, bis infolge von Reibung die Schwingungsenergie aufgezehrt ist. Mit dem mit Wasser gefüllten U-Rohr ist ein Kondensator vergleichbar. Die beiden Elektroden des Kondensators entsprechen den Schenkeln des U-Rohrs. Werden die beiden Platten eines geladenen Kondensators miteinander leitend verbunden, dann wird ein Ladungsausgleich angestrebt, ähnlich dem Flüssigkeitsausgleich in einem U-Rohr. Es ist daher zu erwarten, dass die Kondensatorladung zwischen den beiden Elektroden hin und her schwingt, sobald die Elektroden leitend verbunden werden. Die Schwingung wird solange anhalten, bis die Schwingungsenergie infolge des ohmschen Leitungswiderstands als Wärme abgegeben ist. Es wird eine gedämpfte Schwingung sein.

Quantitative Behandlung der elektrischen  Schwingung

Eine Kombination aus einer Spule und einem Kondensator, wie er in Abb. 3 zu sehen ist, heißt Schwingkreis. Die elektrischen Schwingung, die nach Schließen des Schalters S in diesem  Schwingkreis abläuft, soll nun mit einem kleinen Programm dargestellt werden. Zu der für die Berechnung der jeweiligen Kondensatorladung Q notwendigen Gleichung ( unter der Abb. 3) finden wir, wenn wir in Gedanken den Schwingkreis durchlaufen, zunächst vom Punkt 1 zum Punkt 2 und dann durch die Spule wieder zurück zum Punkt 1. Im ersten Schritt durchlaufen wir die Spannung – Q/C und im zweiten Schritt die Spannung I · R. Die Summe der beiden Spannungen ist gleich der Induktionsspannung  - L · dI/dt. Q steht für die Ladung auf der unteren Kondensatorplatte.

-Q/C + I · R = - L · dI/dt 

Beachte : Die Induktionsspannung ist einer Wirbelspannung ! Die Spannung über der Spule ist nicht gleich der Spannung in der Spule.

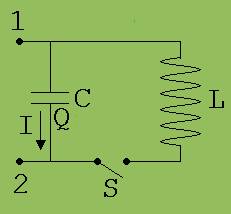
Abb.3

Sind Q und I vor einem kleinen Zeitabschnitt Δt bekannt, dann können die Ladung Q’, die Stromstärke I’  und die Spannung U’ nach Δt berechnet werden.

( Q/C – I · R)  = L · ΔI / Δt    →  ΔI = ( Q/C – I · R)  · Δt / L

I’ = I + ΔI

I’ = I + ( Q/C – I · R)  · Δt / L

Q’ = Q – I · Δt;  U’ = Q’/C

Wenn die Spannung nach Δt  bekannt ist, dann wird  mit den gleichen Rechenschritten die Spannung am Ende des nächsten  Δt berechnet usw..

Nach dem folgenden Programm wird die Spannung am Kondensator in Abhängigkeit von der Zeit unter der Bedingung (Q_Anfang =0,00002C, Δt =0,0001 s, C =2,2E-6 F, L=0,043 H, R=23Ohm) dargestellt:

i = i+(q/c-i*r)*h/a; q= q-i*h; t = t+h; b = q/c; x = t; y = b

i = I, q = Q, h = Δt, a = L, r = R, b = U_Kondensator

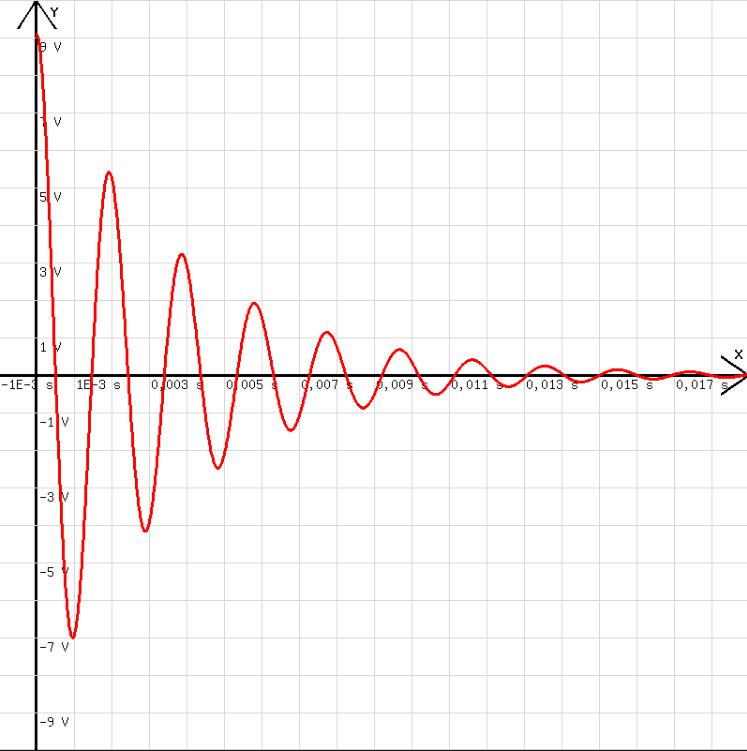
Abb.4

Zum Programm

Mit R= r = 0 Ohm verläuft die Schwingung ungedämpft (siehe Abb. 5). In diesem Fall gilt: Q/C = L · dI / dt , I = - dQ/dt  →  L · d²Q/dt² = -1/C · Q.

Diese Gleichung ähnelt der Gleichung m · d²x/dt² = -D · x, die für einen an einer Schraubenfeder (Federkonstante D) schwingenden Gegenstand (Masse = m) hergeleitet wurde.

m und D entsprechen L und 1/C. Für die Schwingungszeit eines Federpendels gilt: T = 2· π·√(m/D).

Daraus folgt für die elektrische Schwingung: T = 2· π·√(L/(1/C) ) = T = 2· π·√(L·C) . Nach dieser Gleichung gilt für die Schwingungszeit T der hier dargestellten Schwingung:

T = 2· π·√(L·C) = 2· π·√(0,043·2,2E-6) =0,0019 s ≈ 2E-3 s.

Dieser Wert ist am Diagramm in der Abb. 5 ablesbar.

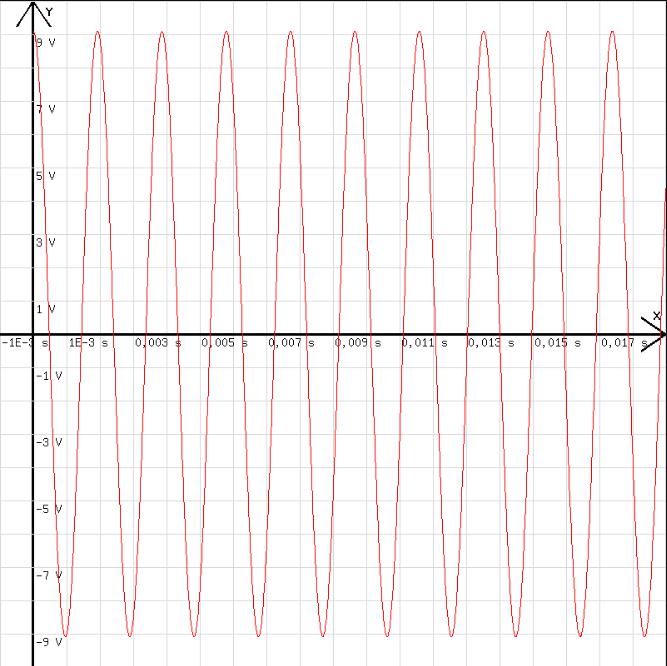
Abb.5

Einstellungen zu Programm

Abb.6