Aus einem Beutel mit 30 weißen und 70 roten Kugeln wird ein Kugel gegriffen und nach Notieren der gezogenen Farbe mit r oder w wieder zurückgelegt. Dies geschieht 10 mal hintereinander. Als Ergebnis dieses Vorgangs liegt dann eine Reihe wie z.B. r r w r w w r r r w vor.
Es stellt sich die Frage: Wie groß ist die Wahrscheinlichkeit, dass wie in diesem Fall 4 weiße und 6 rote Kugeln aus dem Beutel gezogen werden ?
Die Wahrscheinlichkeit für das Ziehen einer weißen Kugel ist p = 3/10, die Gegenwahrscheinlichkeit q = 1-p zur roten Kugel ist 7/10 .
Die Wahrscheinlichkeit, dass sich eine Reihenfolge wie „r r w r w w r r r w“ einstellt ist p4 · q6 . Die Wahrscheinlichkeit, dass genau 4 weiße und 6 rote Kugeln gezogen werden, ist erheblich größer, da verschiedene Reihenfolgen von 4 weißen und 6 roten Würfeln möglich sind.
Wie viele Reihenfolgen j gibt es ?
Es ist oft hilfreich, zunächst eine eine ähnliche, aber leichtere Aufgabe zu lösen. Statt der gegebenen Reihenfolge aus w und r wird die Reihenfolge a, b, c , d , e , f, g , h , i , j gewählt. Die Zahl der möglichen Anordnungen (Permutationen) kann in diesem Fall schnell gefunden werden. Wir beschränken uns zunächst auf die zwei Buchstaben a und b. Es gibt die beiden Anordnungen a, b und b, a. Bei drei Buchstaben a, b , c kann man die möglichen Anordnungen gliedern in 2 mit a, 2 mit b und 2 mit c am Anfang. Es sind insgesamt 2·3 = 6 Möglichkeiten. Zum Verständnis dieser Angabe sei darauf hingewiesen, dass wir die Zahl der Anordnungen mit a am Anfang dadurch erhalten, indem wir von den anderen Buchstaben alle möglichen Anordnungen bilden und jeweils ein a davor setzen. An die Anfangsbuchstaben a, b, c und d können jeweils 2·3 = 6 verschiedene Folgen der anderen Buchstaben angehängt werden. 2·3·4 = 24 verschiedene Anordnungen sind demnach insgesamt möglich.
Für n verschiedene Buchstaben gibt es 1·2·3·4.......· n Möglichkeiten.
Für das Produkt 1·2·3·4.......· n aus den ganzen Zahlen von 1 bis n schreiben wir n! (sprich n Fakultät).
Fakultät = Möglichkeit !
Wir denken nun wieder an j Reihenfolgen aus den Buchstaben r und w. Wenn wir die Buchstaben w und r durch Anhängen von Zahlen unterscheidbar machen, dann können wir durch Vertauschen der Buchstaben w und r aus jeder der aus 4 w und 6 r gebildeten Anordnungen 4! · 6! verschiedenen Reihenfolgen erzeugen und erhalten somit die Gesamtheit aller möglichen Anordnungen aus 10 verschiedenen Zeichen.
Demnach gilt: j · 4! · 6! = 10! → j = 10! / (4! · 6!) = 10! / (4! · (10 - 4)!).
Für die Wahrscheinlichkeit 4 weiße und 6 = 10 - 4 rote Kugeln zu ziehen gilt:
w = [10! / (4! · (10 – 4)!)] · p4 · q6 = [10! / (4! · (10 – 4 )!)] · p4 · (1- p)6 , p = 3/10
Bei m Buchstaben mit k Buchstaben w erhält man entsprechend: w = [m! / [k! · (m - k)!]) ] · pk · (1 - p)(m-k).
p ist die Wahrscheinlichkeit dafür, dass eine weiße Kugel gezogen wird.
Für
(m! / [k! · (m - k)!]) wird
![]() geschrieben.
geschrieben.
Sprich k aus m oder m über k !
Das Diagramm (Binomialverteilung) in der Abb. 1 zeigt die Wahrscheinlichkeiten zu verschiedenen k für den Fall (m =14, p = q = 0,5). Es wird mit m=14; n=20; z=m! / (k!*(m-k)!)*0,5^m; x=k; k=k+1; l=x erzeugt.
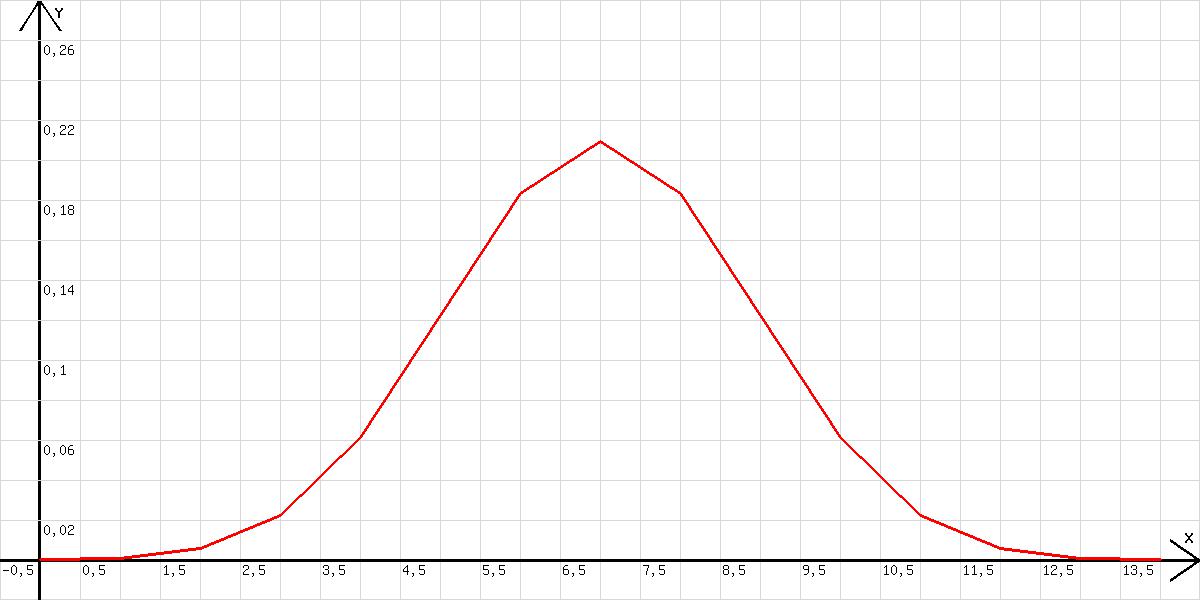
Abb. 1
Mit n=20; x=x+0,01; k=int(x); k=int(x); u=k; v=14!/(k!*(14-k)!)*0,5^14; y=0,21*exp(-0,135*(x-7)^2); l=x wird die Binomialverteilung dargestellt und ihr zugleich der Graph (rot) der Funktion y=a*e-b*(x-m/2)^2 mit a = 0,21 und b = 0,135 angepasst (siehe Abb. 2).
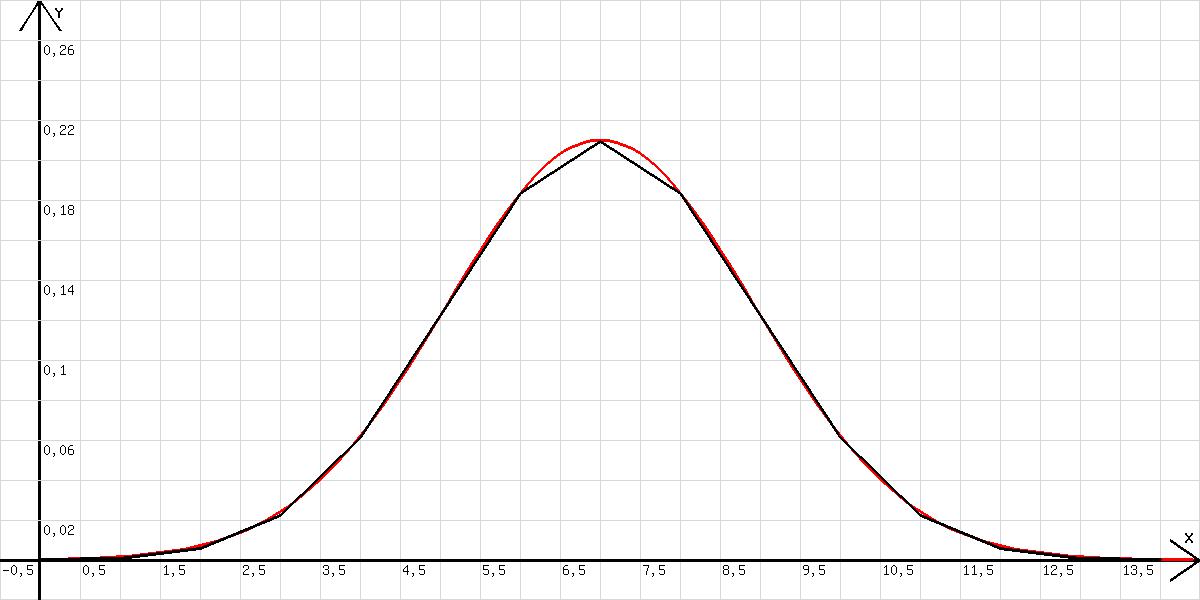
Abb.2
a steht für die Höhe des Diagramms und b ist maßgebend für die Breite. Die Breite nimmt mit wachsendem b ab. In diesem Zusammenhang stellt sich die Frage: In welcher Höhe sollte die Breite gemessen werden ? Die Breitenbestimmung muss zwischen eindeutig definierten Punkten geschehen. In Frage kommen die Wendepunkte der Glockenkurve. Der halbe Abstand dieser Punkte wird σ genannt.
Wendepunkt: Übergang von einer Rechtskurve in eine Linkskurve bzw. einer Linkskurve in eine Rechtskurve. An einem Wendepunkt mit x = xW hat die 1. Ableitung y' ein Extremum und infolgedessen gilt y'' = 0 an einem solchen Punkt.
y = f(x) = a·e-b·(x-m/2)^2 , y' = -a · 2 · b· (x-m/2)·e-b·(x-m/2)^2 ; y'' = -a · 2 · b · e-b·(x-m/2)^2 + a · 4· b2 ·(x-m/2) 2·e-b·(x-m/2)^2
y'' = 0 → -2 · b + 4· b2 ·(xW - m/2)2 = 0 → 1 = 2 · b· (xW - m/2)2 → |xW - m/2| = √( 1/( 2 · b))
Ein Punkt mit x = m/2 halbiert die Abstand der beiden Wendepunkte . |xW – m/2| = σ ist demnach der halbe Abstand der beiden Wendepunkte mit den x- Werten xW und -xW. σ dient als Maß für die Breite.
1 = 2 · b· σ2 → b = 1/(2 · σ2) → σ = √( 1/( 2 · b)
y = a·e-b·(x-m/2)^2 = a·e-0,5·[(x-m/2) / σ]^2
Der Flächeninhalt unter dem Graphen der Exponentialfunktion gleicht dem Flächeninhalt aller in der Abb. 3 sichtbaren Rechtecke mit einer Längeneinheit als Breite. Der Flächeninhalt eines solchen Rechtecks über x = k ist der Größe nach gleich der Wahrscheinlichkeit des zu k gehörenden Ereignisses. Da die Summe aller Wahrscheinlichkeiten gleich 1 ist, folgt: Der Flächeninhalt A der Fläche unter dem Graphen der Exponentialfunktion muss den Wert 1 haben.
|
Abb. 3
|
Die Graphen in der Abb. 3 wurden mit dem folgenden Programm angelegt: u=k+0,5; x=x+0,01; k=int(x);v=14!/(k!*(14-k)!)*0,5^14; y=0,21*exp(-0,135*(x-7)^2); l=x; |
Der Flächeninhalt A unter y= a·e-0,5·[(x-m/2) / σ]^2 unterscheidet sich nicht von dem unter y= a·e-0,5·[x / σ]^2, denn m/2 bewirkt nur eine Verschiebung des Graphen entlang der x -Achse. a·e-0,5·[x / σ]^2 · h ist der Flächeninhalt eines schmalen Rechtecks unter der Glockenkurve mit der Breite Δx = h . x ist die x-Koordinate eines die Grundseite halbierenden Punktes.
A= a ·Σ e- 0,5·[x / σ]^2 · h = a · σ · Σ e- 0,5·[x / σ]^2 · h / σ, x / σ = u, h / σ = Δu
↓
A= a · σ · Σ e- 0,5· u^2 · Δu
Zur Berechnung von Σ e- 0,5· u^2 · Δu wird das Programm „n=10000; S=S+2*exp(-0,5*(u-0,00015)^2)*0,0003; u=u+0,0003;“ im Fenster des hier vorhandenen Rechenprogramms geschrieben.
Wir läuft die Rechnung ( mit Wiederholung) ab?
Das Intervall [0;3] ist gedanklich in Teile Δu = 0,0003 eingeteilt. Zu den Abschnitten werden die Produkte 2*exp(-b*(u+0,00015)^2)*0,0003 gebildet und summiert. Mit dem Faktor 2 vor exp(-b*(x+0,00025)^2) werden die Werte zum Interevall [-3;0] mitgezählt. Die Beschränkung auf das Intervall [0;3] ist angebracht, weil e- 0,5· u^2 für u > 3 kaum von 0 abweicht.
Ergebnis: S = 2,507 → a · σ = 2,507
a hängt der Größe nach von m ab. Diese Abhängigkeit soll nun auch experimentell untersucht werden. Es werden die Höchstwerte a von y=m!/(k!*(m-k)!)*0,5^m für m= 30, 40 und 50 über k = x = m/2 mit dem schon genannten Rechenprogramm bestimmt. In der nächsten Tabelle ist a zu den genannten Werten von m eingetragen.
|
m |
a |
a^2 |
m*a^2 |
|
30 |
0,1446 |
0,02105 |
0,630 |
|
40 |
0,1253 |
0,01562 |
0,625 |
|
50 |
0,1123 |
0,0126 |
0,63 |
Die Tabelle lässt folgenden Schluss zu: m·a2 = 0,63 → a = √ (0,63/m) = 1/√(1,587·m)
1,587 sieht nach 1/2· π aus.
Vermutlich gilt: a = 1/√(0,5· π·m) und nach a · σ · 2,507 = 1 für 1/σ2 = 2,5072 · a2 = 2,507^2 / (0,5· π·m) = 4,00 / m
↓
y = a·e-0,5·[(x-m/2) / σ]^2 = (1/√(0,5· π·m))·e-(2/m)·(x-m/2)^2
Mit dem folgenden Programm können die letzten Aussagen zu verschiedenen Werten m auf ihre Richtigkeit geprüft werden.
m=50;x=x+0,01;k=int(x); u=k; v=m!/(k!*(m-k)!)*0,5^m; y=1/wrz(0,5*pi*m)*exp(-2/m*(x-1/2*m)^2);l=x
Binomialverteilungen und die zu ihrer Beschreibung dienende Exponentialfunktionen werden damit zum Vergleich dargestellt. Für den Fall m = 50 erhält man die in der Abb. 4 sichtbaren Graphen.
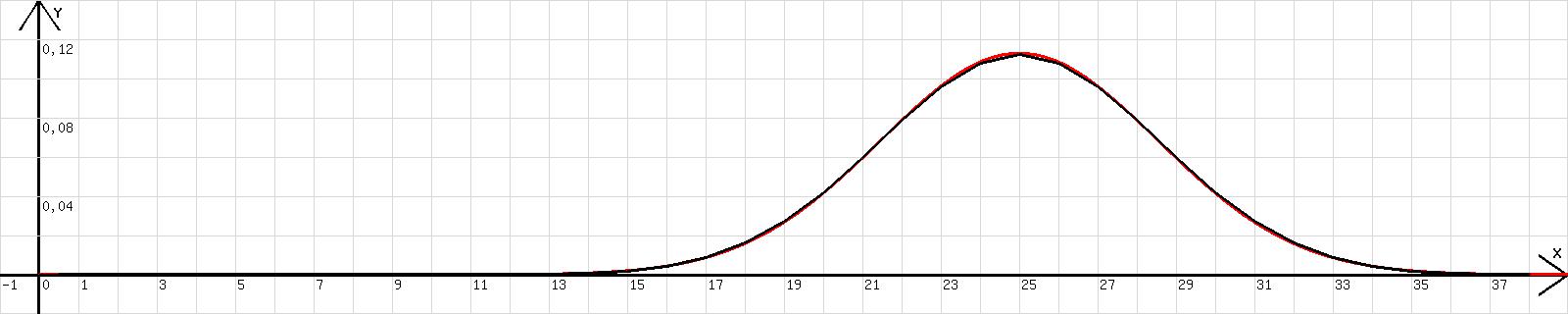
Abb. 4
Wie muss die Funktion y = (1/√(0,5· π·m))·e-(2/m)·(x-m/2)^2 = (1/√(0,5· π·m))·e-(1/(m·0,5))·(x- 0,5·m)^2 geändert werden, wenn sie auch für p≠ 0,5 gelten soll. p· (1-p) muss in die Funktion eingehen, und zwar so, dass die geänderte Funktion für p = 0,5 mit der hier angegebenen Funktion übereinstimmt.
Dies trifft zu, wenn 0,5 durch 2· p· (1-p) ersetzt wird. Diese Korrektur in Bezug auf ein p≠ 0,5 erweist sich nur in (x- 0,5·m)^2 als falsch. In der Klammer darf 0,5 nur durch p ersetzt werden. Mit dem folgenden Programm können die Diagramme in der Abb. 5 erzeugt werden. Die Exponentialfunktion passt sich der Binomialverteilung gut an.
m=30; p=0,3; n =20; x=x+0,01; k=int(x); u=k; v=m!/(k!*(m-k)!)*p^k*(1-p)^(m-k); y= 1/wrz(2*p*(1-p)*pi*m)*exp(-1/(2*p*(1-p)*m)*(x-p*m)^2); l=x
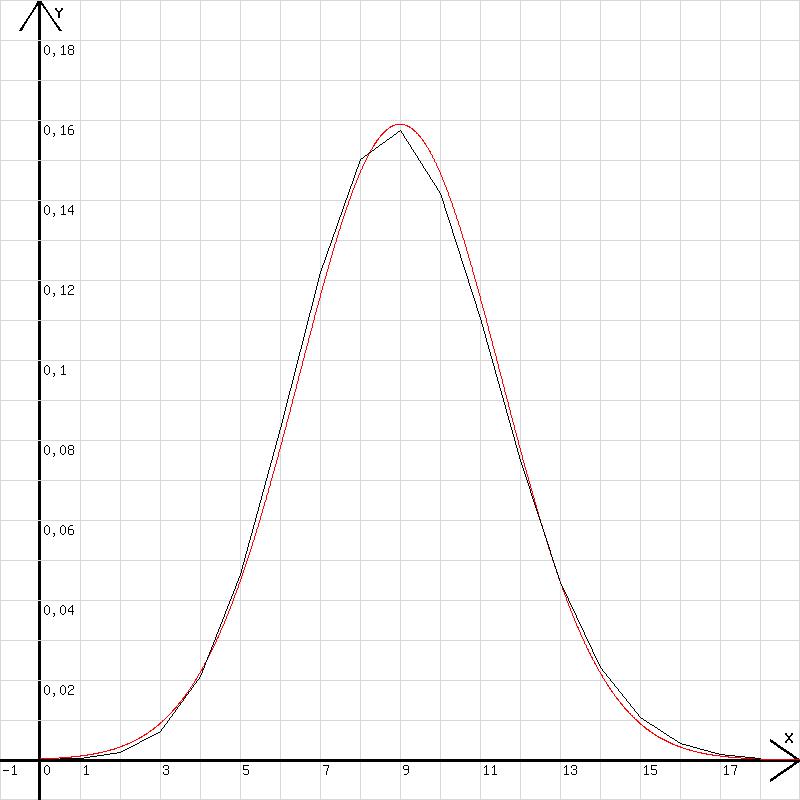
Abb.5
In der Abb.6 ist eine Binomialverteilung mit m = 50 und p = 0,02 (Anfangswert von x = 1) dargestellt. Es ist erkennbar, dass bei kleinem p die Exponentialfunktion (rot) erheblich von der Binomialverteilung abweicht. Wenn p sehr klein ist, dann passt zur Binomialverteilung eine von dem Mathematiker Poisson vorgeschlagene Annäherungsformel .
|
Abb. 6 |
Abb.7 |
m! / [k! · (m – k)!] = m · (m-1) · (m-2).....· (m-k) / k!
Bei einem im Vergleich zu m sehr kleinem k kann geschrieben werden: m · (m-1) · (m-2).....· (m-k) ≈ mk → m! / [k! · (m – k)!] ≈ mk / k!
Wahrscheinlichkeit w(k) ≈ [mk / k! ]· pk ·(1-p)m-k ≈ [mk / k! ]· pk ·(1-p)m = [(m · p)k / k! ] ·(1-p)m
k im Exponent m - k kann gestrichen werden, weil k im Vergleich mit m vernachlässigbar ist.
Wahrscheinlichkeit w(k) ≈ [(m · p)k / k! ] ·(1-p)m = [(m · p)k / k! ] ·[(1-p)1/p] m·p
(1-p)1/p nähert sich mit kleiner werdendem p dem Wert 0,3678776. Es handelt sich um den Kehrwert der Zahl e.
Somit kann für ein kleines p geschrieben werden: w(k) ≈ [(m · p)k / k! ] · e- m·p
Mit dem folgenden Programm wird der Graph zur Binomialverteilung z= (50!/[ x!·(50-x)!]·0,02x ·(1- 0,02)(100-x) mit der dazu passenden Graphen der Funktion y = ( (p·m)x / x!) · e (-p · m) verglichen. Es sind kaum Abweichungen voneinander zu erkennen (siehe Abb. 7),
n=20;x=x+1;p=0,02;m=50;y=((p*m)^x/x!)*e^(-p*m); z=m!/(x!*(m-x)!)*(p^x)*(1-p)^(m-x);l=l+1
Über die Verteilung von Messfehlern
Wir gehen davon aus, dass Messfehler f Summen aus m sehr kleinen mit der Wahrscheinlichkeit p = 0 ,5 auftretenden Fehlern fe und fe' sind. fe vergrößert einen Messwert und fe' verkleinert ihn (er ist negativ). f ist demnach gleich einer Summe aus fe und fe'. Bei vielen Messungen mit jeweils m Fehlern wird sich eine Binomialverteilung der fe und fe' einstellen. Setzt sich ein Fehler f aus k Werten der Größe fe und m-k Werten der Größe fe' zusammen, dann gilt:
f = h·k + (m-k)·h' = h·k – (m-k)·h = 2 · h·k - m·h → f /(2·h) = k - m/2 = k - p·m
h und h' sind die Mittelwerte von fe und fe', für die vermutlich h' = -h gilt.
Die Wahrscheinlichkeit des Fehlers f ist demnach W(f) = 1/√(p· π·m)·e-[1/(p·m)]·(k-p·m)^2 = 1/√(p· π·m)·e-[1/(p·m)]·[f/(2·h)]^2 . Fehler f mit gleichen k gehören zu einem Intervall der Breite 2·h, denn wenn sich k um 1 ändert, dann ändert sich der zugehörende Fehler f um 2·h.
W(f) = [1/√(p· π·m)]·e-[1/(p·m)]·[f/(2·h)]^2 ist die Wahrscheinlichkeit, mit der ein Fehler f in ein Intervall der Breite 2·h fällt.
Experimentelle
Untersuchung der Fehlerverteilung
Ein 2000 Hz - Ton wird mit einem Mikrofon aufgenommen und nach Verstärkung des Signals auf ±1,5V mit Hilfe Rechners mit AD-Wandler (CASSY - E) registriert (siehe Abb. 8). Durch eine gegen das Messsignal wirkende konstante Gegenspannung erreicht man, dass die positiven Halbwellen höchstens 0,5 V erreichen (siehe Abb.9 ). So können die Höhen der Spannungsspitzen in den empfindlichen Messbereichen ±1V und ± 0,3 Volt gemessen werden, in denen die Schwankungen des Messsignals gut erkennbar sind. Je Sekunde werden 2000 Spannungsspitzen ausgemessen. Der Messbereich wird vom Rechner in 256 gleich große Intervalle aufgeteilt. Über jedem Intervall errichtet der Computer auf seinem Bildschirm eine senkrechte Strecke, deren Länge proportional zur Zahl der Messwerte ist, die je Sekunde in dieses Intervall fallen (Zahl aller Messwerte im Intervall / Zeit der Messwertaufnahme).
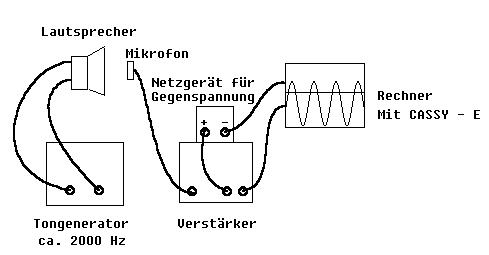
Abb. 8
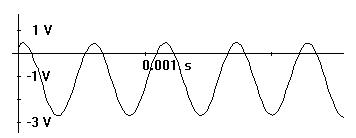
Abb. 9
In den Abb. 10 und 11 sind Ergebnisse dargestellt, die im Messbereich ±1V aufgenommen wurden. Deutlich ist zu sehen, wie die Diagramme mit zunehmender Anzahl von Messungen mehr und mehr eine Glockenform annehmen.
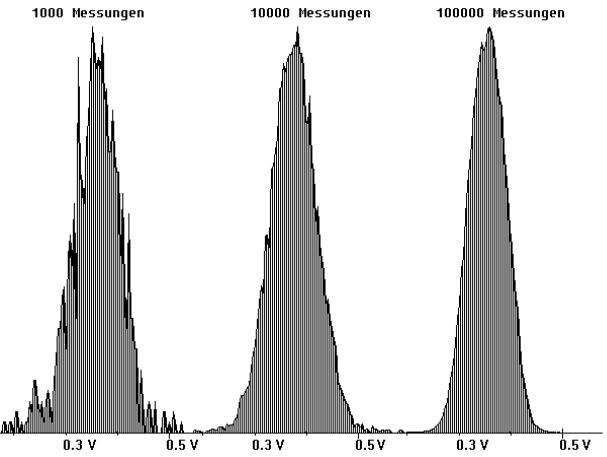
Abb. 10
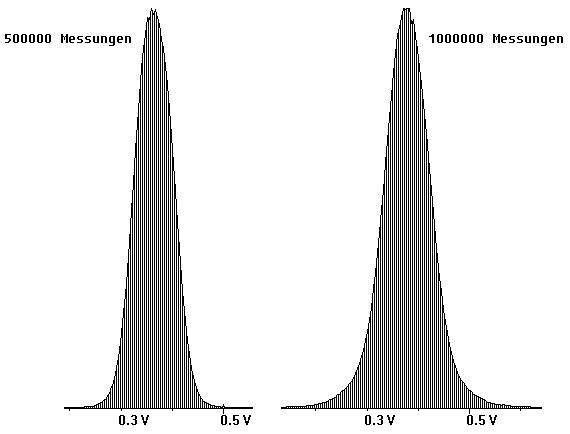
Abb. 11