Über das Auslaufen einer Badewanne

Eine quaderförmige Badewanne mit dem Querschnitt A = 0,8 m² läuft durch eine Öffnung am Boden mit dem Querschnitt B aus.

B = 10 cm² = 0,001 m², anfängliches Wasservolumen = 0,15 m³.

Abb.1

1. Mit welcher Geschwindigkeit tritt das Wasser aus dieser Öffnung ?

2. In welcher Zeit wird die Badewanne geleert ?

Diese beiden Fragen können mit Hilfe des Energiesatzes beantwortet werden. Auf die Frage 1 ist schnell eine Antwort gefunden. Wenn eine kleine Wassermenge der Masse m’ ausläuft, dann fehlt sie an der Oberfläche des Wassers. Die potentielle Energie des Wassers nimmt um m’·g · x ab (x = Höhe des Wasserspiegels). Das unten austretende Wasser hat die kinetische Energie m’ ·v² /2 . Nach dem Energieerhaltungssatz gilt:

m’ ·v² /2 = m’ · g · x → v = √( 2 · g · x )

x ·A = V  → x = V/A, v = √( 2 · g · x)  → v = √( 2 · g · V/A )

Die kinetische Energie des Wassers infolge der Sinkgeschwindigkeit ist vernachlässigbar klein. Aus dem Wasservolumen V und dem Querschnitt A der Badewanne kann der Wasserstand x errechnet werden. Nach einem kleinen Zeitabschnitt Δt = h hat das Volumen der Wassers um v · Δt ·B abgenommen (siehe Abb. 2).

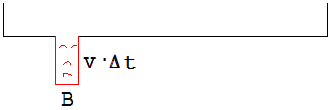
Abb.2

Für das Volumen V' nach Δt gilt: V' = V - √( 2 · g · V/A ) ·B · Δt.

In Abb. 3 ist zu sehen, dass eine Wanne mit einem Querschnitt A =0,8 m² , welche anfangs 0,15 m³  Wasser enthält, in ca. T =155 s durch ein Loch mit dem Querschnitt B = 10 cm² = 0,001 m²  leer läuft.

Mit y=y-wrz(2*9,81*y/0,8)*0,001*h;x=x+h;l=x; wird das Volumen (V=y, A = 0,8 m², B =0,001 m²) in Abhängigkeit von der Zeit angezeigt.

Als Anfangswert von y muss 0,15 eingetragen werden.

Mit y=y-wrz( 2*9,81*y/0,8 )*0,001*h;x=x+h;l=x; w=6,25E-6*(x-155)^2 wird außerdem noch eine Parabel dem Auslaufdiagramm angepasst (siehe Abb. 4).

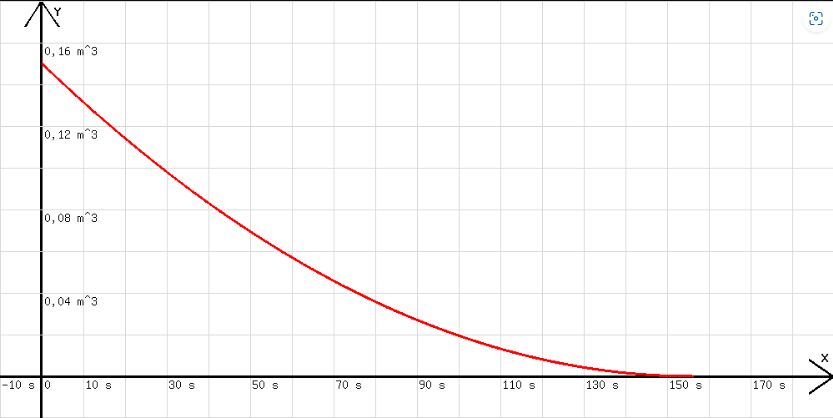
Abb.3

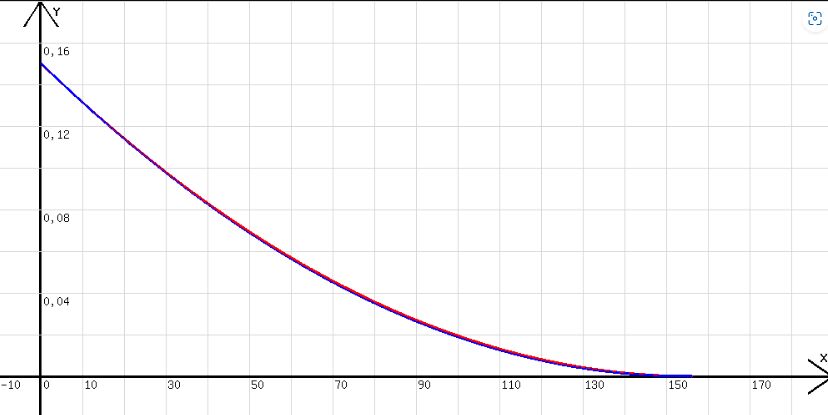
Abb. 4

Einstellungen für das Programm

Zum Programm

Abb.5

In der Abb. 6 ist ein Messdiagramm  zu sehen, welches von einem Schüler (Adalbert-Stifter-Gymnasium in Passau)  im Rahmen einer Facharbeit mit Hilfe der Experimentierwippe aufgenommen wurde. Der Schüler ließ ein an der Schmalseite der Experimentierwippe hängendes,  mit  Wasser gefülltes zylindrisches Gefäß ( Durchmesser = 8 cm) mit einem Loch im Gefäßbodenboden (Durchmesser 3,2 mm) leer laufen. Die Wippe diente in diesem Fall als elektrische Waage. Dem Diagramm ist eine Parabel nach V = f(t) = 0,067 ml/s² ·(88 s – t)² angepasst.

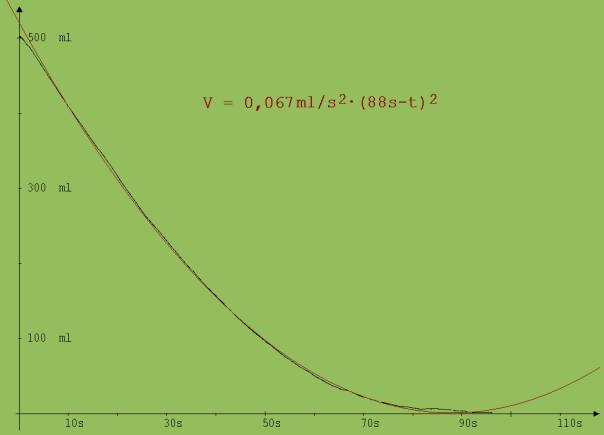
Abb.6