Differentiation von y=sin(x) und y = cos(x)

y = sin(x) , x = Bogenmaß!

Δy/Δx = [sin(x+ Δx) - sin(x)] / Δx = [{sin(x)*cos( Δx)+ sin( Δx) *cos(x)}- sin(x)] / Δx

Angewandt wurde das Additionstheorem zu sin(α+β): sin(α+β)= sin(α)*cos(β)+ sin(β)*cos(α) !

Δy/Δx = [sin(x)*cos( Δx)-sin(x)] / Δx +sin( Δx) *cos(x) / Δx

Δy/Δx = sin(x) *(cos( Δx) - 1)/ Δx + cos(x)*sin( Δx) / Δx

Behauptungen: lim { (cos( x) - 1)/ x} _{x→ 0} =0 , lim {sin(x) / x} _{x→ 0} =1 → lim {Δy/Δx} _{Δx→ 0} = dy/dx = cos(x)

Beweis zu lim { (cos( x) - 1)/ x} _{x→ 0} = 0

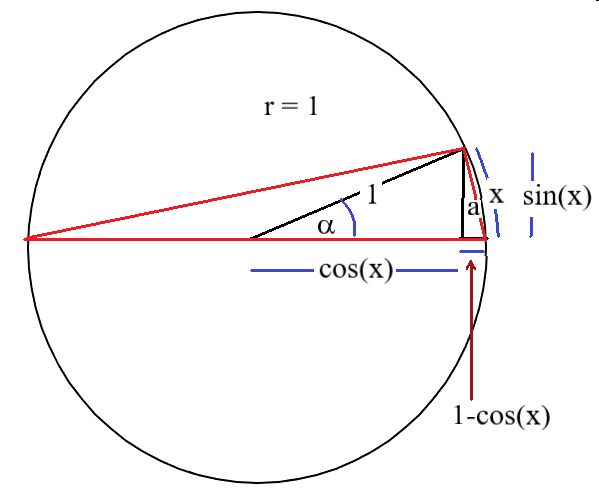
Nach der Abb. 1 gilt: ( 1- cos( x)) * 2 = a² ( Kathetensatz !) → ( 1 - cos( x)) * 2/x = a*a/x

Mit x → 0 strebt a/x gegen 1 und a gegen 0. Folglich strebt (1 - cos( x) ) * 2/x = a*a/x gegen 0.

Folglich gilt auch lim { (cos( x) - 1)/ x} _{x→ 0} = 0.

Beweis zu lim sin( x) / x} _{x→ 0} = 1

sin(x)² = a² - (1 - cos(x))² ( Pythagoras !) → sin(x)² / x² = a² / x² - (1 - cos(x))² / x² .

(1 - cos(x))² / x² strebt im Fall x → 0 gegen 0, a² / x² strebt im Fall x → 0 gegen 1.

Somit gilt: lim {sin(x) / x } _{x→ 0} =1.

y = cos(x)

Δy/Δx = [cos(x+ Δx) - cos(x)] / Δx = {[cos(x)*cos( Δx) – sin(x)* sin( Δx)] - cos(x)} / Δx

Angewandt wurde das Additionstheorem zu sin(α+β): cosα+β)= cos(α)*cos(β) - sin(β)*sin(α) !

Δy/Δx = cos(x)*(cos( Δx) -1) / Δx – sin(x) * sin( Δx)/ Δx

Somit gilt: lim { Δy/Δx} _{x→ 0} = - sin(x) → dy/dx = - sin(x)

Abb.1

y =sin(b*x)

Behauptung: dy/dx = b*cos(b*x).

Beweis:

lim {[sin(b*x- Δ(b*x)) - sin(b*x)] / Δ(b*x)} _{x → 0} = cos(b*x)

dy/dx = lim {[sin(b*x- Δ(b*x))- sin(b*x)] / Δx} _{x → 0} = lim {b*[sin(b*x- Δ(b*x)) - sin(b*x)] / Δ(b*x)} _{x → 0} = b*cos(b*x)

Folglich gilt: dy/dx = b*(cos(b*x)

Entsprechend gilt für y=b*cos(b*x): dy/dx = b*(-sin(b*x))