Gewinnwahrscheinlichkeiten beim Lottospiel

Beim Lottospiel werden 6  Zahlen in einem Feld mit den Zahlen 1 – 49 angekreuzt. Werden bei der Ziehung der Lottozahlen diese 6 angekreuzten Zahlen ausgewählt, dann hat der Spieler einen Hauptgewinn mit dem Ereignis A₆ erzielt. Gewinne fallen auch dann an, wenn nur 5, 4 oder 3 der angekreuzten Zahlen gezogen werden.

Wie groß sind die Wahrscheinlichkeiten P(A₆), P(A₅),  P(A₄),  P(A₃)   dieser Gewinne ?

A₆ wird nur durch ein einziges Ergebnis realisiert.

   P(A₆) = 1 / j ;     j  = Zahl aller möglichen Ergebnisse

Ein Ergebnis kann wie folgt dargestellt werden:

1 (0); 2(0); 3 (#); ………..33(#); 34 (0);………49(#)

Die nicht vom Spieler ausgewählten Zahlen werden mit einem Kreuz, die anderen  mit einer 0 markiert. Die Zahl der möglichen Ergebnisse gleicht der Zahl der Anordnungen (Permutationen), die für 43 Nullen und 6 Kreuze möglich sind. 

Wie kann man die Anzahl j solcher Anordnungen berechnen ?

Eine Antwort hierauf kann zunächst nicht gegeben werden.

Vielleicht ist es hilfreich, wenn es gelingt,  eine ähnliche Aufgabe zu lösen.  Die Nullen und Kreuze kann man durch 49 verschiedene Buchstaben  a, b, c, d, e, f …A, B …ersetzen.  Möglicherweise kann unter diesen Bedingungen die Zahl der Anordnungen gefunden werden. Wir beschränken uns zunächst auf die zwei Buchstaben a und b. Es gibt die beiden Anordnungen a, b und b, a.  Bei drei Buchstaben a, b , c  kann man die möglichen Permutationen (Permutation =Vertauschung) gliedern in 2 Permutationen mit a , 2 Permutationen mit b und 2 Permutationen mit c am Anfang.  Es sind insgesamt 2·3 = 6 Möglichkeiten.   Zum Verständnis dieser Angabe sei darauf hingewiesen, dass wir die Zahl der Anordnungen mit a am Anfang dadurch erhalten, indem wir von den anderen Buchstaben alle möglichen Permutationen bilden und jeweils ein a davor setzen.  Nach Einteilung der Permutationen von vier Buchstaben a, b, c, d nach deren Anfangsbuchstaben fallen vier Gruppen mit je 2·3 = 6 verschiedenen Folgen an.  Es sind insgesamt 2·3·4 = 24 Möglichkeiten.

    Für n verschiedene Buchstaben gibt es 1·2·3·4.......·n Möglichkeiten.

Für das Produkt aus den ganzen Zahlen von 1 bis n schreiben wir n! (sprich n Fakultät)

Fakultät = Möglichkeit ! 

Wir wenden uns nun wieder der Reihenfolge aus Nullen und Kreuzen zu. Aus jeder der j möglichen Anordnungen mit 6 Kreuzen und 43 Nullen können wir 6! verschiedenen Anordnungen erzeugen, wenn wir die Kreuze nummerieren und dann vertauschen. Nach Unterscheidung der Kreuze gibt es insgesamt j · 6! verschiedenen Permutationen. Aus jeder dieser j  · 6! Anordnungen können nach Nummerierung der Nullen  insgesamt 43! verschiedene Folgen erzeugt werden. Nach dieser neuen Unterscheidung gibt es insgesamt j ·6! ·43! Permutationen.

 j ·6! ·43 ! ist die Gesamtzahl der Permutationen von 49 verschiedenen Zeichen. 

    j ·5! ·43 ! = 49!        →       j = 49/[ 6! ·(49-6)!]

Bei n Elemente mit m Nullen und k Kreuzen erhält man:

j = n! / [k! · m!] = n! / [k! · (n-k)!]

’

Nun kann P(A₆) berechnet werden.

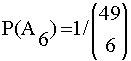
P(A₆) = 6! · 43! / 49! =1/13983816  » 1/ 14000000

Die Berechnung der anderen Gewinnwahrscheinlichkeiten  ist etwas schwieriger, da A₅ , A₄ und A₃ durch viele Ergebnisse realisiert werden. Ein zu A₅ gehörendes Ergebnis ist eine Auswahl von 5 richtigen Zahlen aus 6 richtigen Zahlen in Verbindung mit einer Zahl unter den 43 anderen falschen Zahlen. Da es insgesamt 6! / (5 ! · 1!) Fünferkombinationen aus 6 richtigen Zahlen gibt und diese Kombinationen mit 43 verschiedenen anderen Zahlen kombiniert werden können , gilt für P(A₅):

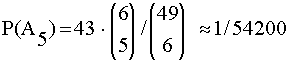
Ein zu A₄ gehörendes Ergebnis erhält man, indem man aus den 6 richtigen Zahlen 4 Zahlen auswählt und diese Kombination dann mit einer Zweierkombination aus den 43 falschen Zahlen verbindet.  Da es insgesamt 6! / (4 ! · 2!) Viererkombinationen aus 6 angekreuzten Zahlen gibt und diese Kombinationen mit 43! /( 2! · 41!) verschiedenen Zweierkombinationen verbunden werden können , gilt für P(A₄):

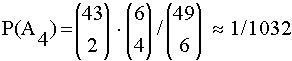
Ein zu A₃ gehörendes Ergebnis erhält man, indem man aus den 6 richtigen Zahlen 3 Zahlen auswählt und diese Kombination dann mit einer Dreierkombination aus den 43 falschen Zahlen verbindet. Da es insgesamt 6! / (3 ! · 3!) Dreierkombinationen aus 6 richtigen Zahlen gibt und diese Kombinationen mit 43! /( 3! · 40!) verschiedenen Kombinationen aus 43 Zahlen verbunden werden können , gilt für P(A₄):

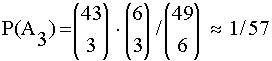
Anmerkung: Zur Berechnung von n über k wird im Rechenfenster von „Mathe.-Physik“  n#k eingegeben. So wird P(A₃)  mit   43#3 · 6#3 / 49#6 berechnet.