­4.2 Varianz und Standardabweichung

Es ist nun zu verstehen, dass ein einzelner Messwert nicht zur Beschreibung einer Größe (Länge, Kraft, Wahrscheinlichkeit ...) geeignet ist. Auch ein Mittelwert M vermittelt nur dann eine Vorstellung von einer Größe, wenn  neben ihm noch eine Angabe über den möglichen zufälligen Fehler gemacht wird.

Wie soll dies geschehen ?

Zu dieser Frage ist ein Messbeispiel hilfreich. Es vermittelt ein Bild über die Verteilung zufälliger Fehler. Das folgende Experiment ist als Beispiel geeignet. Es werden dabei Mittelwerte aus relativen Häufigkeiten (Messwerten der Wahrscheinlichkeit) gebildet.

Das Programm P₁ unter diesen Zeilen wird in das Rechenfenster des hier vorhandenen Rechenprogramms kopiert. Mit ihm wird 10000 mal ein Würfelspiel mit jeweils 40 Würfen simuliert (Ergebnisse sind die gleich wahrscheinlichen Zahlen von 1 bis 6). Dazu werden die absoluten Häufigkeiten z einer 6 sowie die relativen Häufigkeiten x = z/40 bestimmt.

zuf(6) erzeugt diese Zufallsergebnisse. Die Funktion st1() in den Programmzeilen liefert für einen Wert w (0<=w<1) den Wert 1 und andernfalls den Wert 0.

Mit a=st1((x-0,025)*40)+a = st1((x-0,025)/0,025)+a werden die demnach relativen Häufigkeiten x =z/40 (0<=x <0,25) gezählt und mit b=st1((x-0,025)*40)+b alle Werte x =z/40 (0<=x <0,25) usw..

P₁: n=10000;l=l+1;z=0;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z; z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z; z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z; z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z; z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z; z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z; x=z/40;u=u+x;w=u/10000;a=st1((x)*40)+a;b=st1((x-0,025)*40)+b;c=st1((x-0,05)*40)+c;d=st1((x-0,075)*40)+d;f=st1((x-0,1)*40)+f; g=st1((x-0,125)*40)+g;h=st1((x-0,150)*40)+h;i=st1((x-0,175)*40)+i;j=st1((x-0,2)*40)+j;k=st1((x-0,225)*40)+k;m=st1((x-0,25)*40)+m;o=st1((x-0,275)*40)+o;p=st1((x-0,3)*40)+p;q=st1((x-0,325)*40)+q;r=st1((x-0,35)*40)+r;s=st1((x-0,375)*40)+s;t=st1((x-0,4)*40)+t;

P₁ wird nach seinem Ablauf gelöscht, das Tabellenfenster geleert und im Variablenfeld wird L auf 0 gesetzt. Danach wird das folgende Programm P₂ in das Programmfenster des Rechners übertragen (kopieren/einfügen).

P2: n=17;y=st1(l)*a+st1(l-0.1)*b+st1(l-1,1)*c+st1(l-2,1)*d+st1(l-3,1)*f+st1(l-4,1)*g+st1(l-5,1)*h+st1(l-6,1)*i+st1(l-7,1)*j+st1(l-8,1)*k+st1(l-9,1)*m+st1(l-10,1)*o+st1(l-11,1)*p+st1(l-12,1)*q+st1(l-13,1)*r+st1(l-14,1)*s+st1(l-15,1)*t;x=l*0,025;l=l+1

Mit diesen Zeilen wird im Tabellenfenster eine Tabelle erstellt, wie sie neben der Abb.1 zu sehen ist. Die erste Zeile dieser Tabelle zeigt an, dass 58 mal x=z/40 kleiner als 0,025 ist. Dann ist zu sehen, dass x ( 0,025<=x<0,05) 206 mal und x (0,05 <=x<0,075) 527 mal vorkommt usw.. Diese Tabelle wird zur grafischen Darstellung in das Tabellenfenster des hier vorhandenen Grafikprogramms Sim.html übertragen. Mit diesem Programm werden nicht nur die Wertepaare der obigen Tabelle durch Kreuze dargestellt (P hinter die erste Tabellenzeile schreiben !), es wird auch noch der Graph der Funktion y= 1700*exp(-145*(x-0,166)^2) diesen Kreuzen angepasst (siehe Abb.1).

Die Wertepaare passen gut zu der Exponentialfunktion, die durch eine Glockenkurve dargestellt wird. Diese Kurve hat ihr Maximum über dem Mittelwert 0,166.. = 1/6 aller relativen Häufigkeiten x .

Es wird davon ausgegangen, dass eine exponentiellen Fehlerverteilung nach A·e^{-b·f^2} ( f = x-0,166) für jede Art von Messung gilt, weshalb es sinnvoll erscheint, an ihr ein geeignetes Maß für deren Ungenauigkeit zu suchen. Je breiter die Kurve ist, desto größer sind die Abweichungen der Messwerte. Aus einer Angabe ihrer Breite kann auf die Genauigkeit der Messwerte geschlossen werden. In welcher Höhe sollte die Breite gemessen werden. Die Breitenbestimmung muss zwischen eindeutig definierten Punkten geschehen. In Frage kommen die Wendepunkte der Glockenkurve,

Wendepunkt: Übergang von einer Rechtskurve in eine Linkskurve bzw. einer Linkskurve in eine Rechtskurve. Die 1. Ableitung von f(x) hat an einem Wendepunkt ein Extremum.

Der Abstand B der Wendepunkte kann nur dann als sinnvolles Maß für die Genauigkeit der Messwerte eingeführt werden, wenn mit einer zumutbaren Zahl von Messwerten ohne großen Aufwand auf B geschlossen werden kann. Dies ist möglich, denn es kann mit Hilfe des Programms P₃ gezeigt werden, dass (B/2)² gleich dem Mittelwert aus den Quadraten der Fehler f (f = x-wahrer Wert W) ist.

B/2 = σ (Sigma) = √ (Mittelwert von f²)

Der Mittelwert von f² heißt Varianz der Messwerte und die Wurzel daraus heißt Standardabweichung oder mittlerer Fehler .

P₃: n=10000;l=l+1;z=0;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z; z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z; z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z; z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z; z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z; z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;x=z/40;u=(x-0,166)^2+u; w=u/10000;y=W

Mit diesem Programm wird für die Varianz 0,00346522 und für die Wurzel aus dem Mittelwert von f² der Wert 0,058866 gefunden. Dieser Wert stimmt mit dem an dem Graphen ablesbaren Wert B/2 überein.

Wie viele Werte unter den 10000 relativen Häufigkeiten haben ein f (|f| <= σ) ?

Zur Beantwortung dieser Frage wird das folgende Programm P₄ in das Rechenfenster von Rechenprogramms eingefügt. P₄ lietert mit der Varianz 0,00346522 einen Wert ≈ 0,69. Demnach haben ca. 69% aller Messwerte ( relativen Häufigkeiten) einen Fehler <= σ

P₄: n=10000;l=l+1;z=0;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z; z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z; z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z; z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z; z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z; z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;z=int(zuf(6)/6)+z;x=z/40;u=st1((x-0,16666666)^2/0,00346522)+u;w=u/10000

Für die Aussage, dass Messfehler nach A·e^{-b·f^2} verteilt sind, sprechen auch die Ergebnisse des folgenden Experiments (siehe Abb.2). Ein 2000 Hz - Ton wird mit einem Mikrofon aufgenommen. Aus diesem auf ±1,5V verstärkten Signal wird durch eine Gegenspannung das Signal (±1,5 -1)V . Es wird mit dem AD-Wandler (CASSY - E) registriert. Durch die konstante Gegenspannung wird erreicht, dass die positiven Halbwellen nicht über 0,5 V hinausgehen (siehe Abb.3 ). So können die Höhen der Spannungsspitzen in den empfindlichen Messbereichen ±1V und ± 0,3 Volt gemessen werden, in denen die Schwankungen des Messsignals gut erkennbar sind. Je Sekunde werden 2000 Spannungsspitzen gemessen. Der Messbereich wird vom Rechner in 256 gleich große Intervalle aufgeteilt. Über jedem Intervall errichtet der an das CASSY-E angeschlossene Rechner auf seinem Bildschirm eine senkrechte Strecke, deren Länge proportional zur Zahl der Messwerte ist, die je Sekunde in dieses Intervall fallen (Zahl aller Messwerte im Intervall / Zeit der Messwertaufnahme).

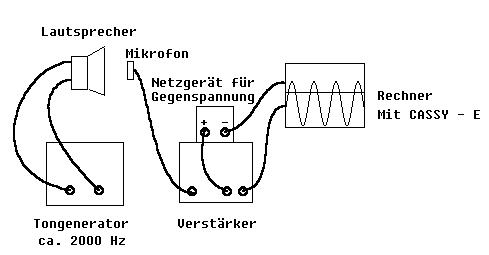
Abb.2

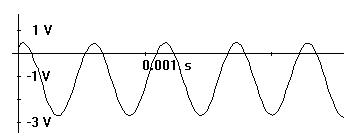
Abb.3

In den Abb. 4 und 5 sind Ergebnisse dargestellt, die im Messbereich ±1V aufgenommen wurden. Deutlich ist zu sehen, wie die Diagramme mit zunehmender Anzahl von Messungen mehr und mehr eine Glockenform annehmen.

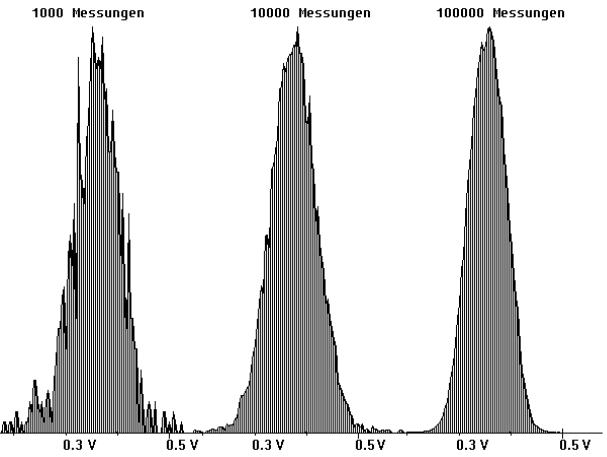
Abb. 4

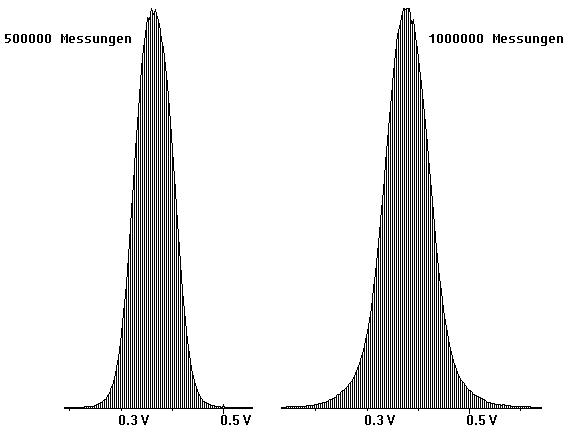
Abb. 5

Eine mathematische Untersuchung wird an dem Diagramm in Abb. 6 durchgeführt. Diese Verteilungskurve zu 1000000 Messungen, welche die Spitzen der erwähnten Strecken verbindet (hier unsichtbar), wurde mit der Gegenspannung -1,374V in dem Messbereich ±0,3V aufgenommen. Auch auf diese Kurve passt ein Graph der Form f(x) = A·e^{-b·(x-W)^2} . f(x) steht für die Zahl der Messwerte einem Intervall um einen Messwert x. W ist der „wahre Wert“ 0,126 V und (x-W) ist der Fehler f des Messwerts.

Für B/2 = σ (Sigma) gilt auch in diesem Fall; σ = √ (Mittelwert von f²) .

Die geschweifte Kurve unterhalb der Glockenkurve beschreibt die 1. Ableitung der Exponentialfunktion, Ihr Maximum und ihr Minimum weist auf die Wendepunkte hin, An den Wendepunkten ist der Graph am steilsten. Demnach ist die 2.Ableitung der Exponentialfunktion an den Wendepunkten gleich 0. Diese Tatsache ermöglicht die Berechnung von σ .

y = f(x) = A·e^{-b·(x-W)^2} , y' = -A · 2 · b· (x-W)·e^{-b·(x-W)^2} ; y'' = -A · 2 · b · e^{-b·(x-W)^2} + A · 4· b² ·(x-W) ²·e^{-b·(x-W)^2}

An den Wendepunkten mit (x- W)² = σ² gilt: y'' =0.

y'' = -A · 2 · b · e^{-b· σ^2} + A · 4· b² ·σ ²·e^{-b· σ^2} = 0 → 1 = 2 · b· σ² → σ = √( 1/( 2 · b))

b = 280 → σ = 0,042 V

Dieser Wert gleicht dem am Diagramm messbaren σ.

In A·e^{-b·f^2} kann b durch 0,5 · 1/ σ² ersetzt werden

A·e^{-b·f^2} = A·e^{- 0,5 · (f/ σ)^2}

f/σ heißt standardisierter Zufallsfehler fs.

A·e^{-b·f^2} = A·e^{- 0,5 · fs^2}

Wie groß ist die Wahrscheinlichkeit für einen Fehler |f|<= σ bzw. |f_s| <= 1?

Die Wahrscheinlichkeit p, mit der ein Messwert mit einem Fehler |f_s| <=1 behaftet ist, erhält man, indem man die Zahl der zum Intervall (-1<=f_s<=1) gehörenden Messwerte y durch die Zahl aller Messwerte z teilt ( P =y/z). Hierbei wird eine sehr große Zahl von Messwerten vorausgesetzt.

Mit steigender Zahl von Messwerten z passt sich das Diagramm zur Häufigkeitsverteilung immer besser dem A·e^{-0,5·fs^2} - Graphen an. Daraus kann geschlossen werden, dass die relative Häufigkeit y/z für ein Ereignis mit |f_s| <= 1 mit steigender Zahl der Messwerte gegen den Quotienten B/C strebt. B ist der Flächeninhalt der Fläche zwischen dem Intervall [-1; +1] und der Glockenkurve. C ist der Flächeninhalt der gesamten Fläche zwischen der x-Achse und der Glockenkurve.

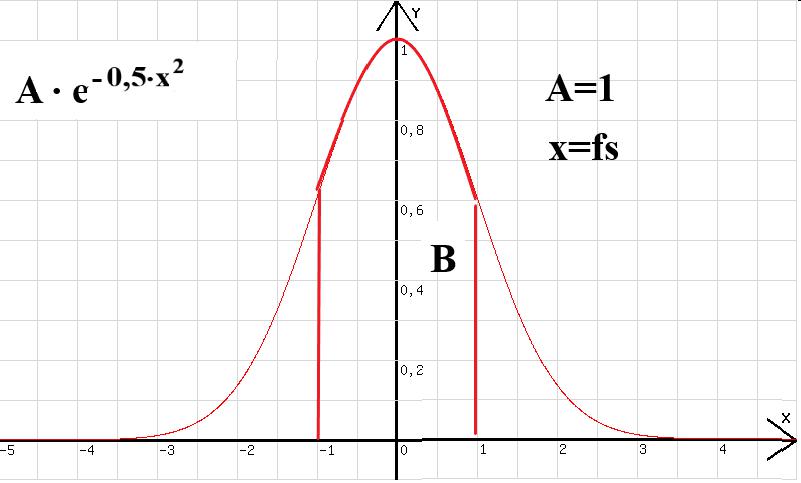
Abb.8

Wahrscheinlichkeit p = B/C = b/ c, b=B/2, c= C/2

Die Berechnung von b und c geschieht nach Einstellung auf „mit Wiederholung“ mit den Programmen P5 und P6.

P₅: n=1;b=exp(-0,5*(x+0,005)^2)*0,01+b; x=x+0,01;l=x;

P₆: n=5;b=exp(-0,5*(x+0,005)^2)*0,01+b; x=x+0,01;l=x;

Mit P₅ und P₆ werden Flächeninhalte von Rechtecken summiert. Die x-Achse wird von x =0 bis x = 5 in Intervalle der Länge 0,01 aufgeteilt. Über jedem Intervall wird ein Rechteck errichtet, welches über der Mitte des Intervalls an den Graphen von y = e ^{-0,5*x^2} stößt. Mit P₅ werden die Flächeninhalte aller Rechtecke summiert die auf dem Intervall [0;1] stehen. Die Summe kann mit b gleichgesetzt werden. Mit P₆ werden die Flächeninhalte aller Rechtecke summiert die auf dem Intervall [0;5] stehen. Die Summe kann mit c gleichgesetzt werden.

Die angegebenen Programme liefern für b =0,085 und für 1,253313418864 → b/c = 0,067820226545602≈ 68%

Im Fall A<> 1gilt: b/c = (A· 0,085)/(A· 1,253313418864) = 0,085/ 1,253313418864

Die Wahrscheinlichkeit p ist unabhängig von A ≈ 68%

Ergebnis:

Bei sehr vielen Messwerten fallen 68% der Werte in den Bereich W± σ. Das heißt ein Messwert M hat mit der Wahrscheinlichkeit 0,68 einen Fehler f mit einem Betrag ≤ σ.

Der mittlere Fehler des Mittelwerts

Der mittlere Fehler σ von n Messwerten ist größer als der entsprechende Fehler σ_M von n Mittelwerten aus je n Einzelwerten einer Folge von Messwerten.

Kann von σ auf σ_M geschlossen werden ?

Werden n Messwerte mit den Fehlern f₁ , f₂........f_n gemittelt, dann ist [(f₁+f₂......+f_n)/ n]² das zum Mittelwert gehörende Fehlerquadrat.

[(f₁+f₂......+f_n)/ n]² = [f₁² + f₂² + f₃² ….+ f_n² + 2·(f₁·f₂ + f₁·f₃ + f₁·f₄ ..+ f₂·f₃ + f₂·f₄ + f₂·f₅ …..)]/ n²

Bei großem n heben sich die Produkte in den runden Klammern gegenseitig auf, da z.B. das Produkt f₁·f₂ ebenso wahrscheinlich ist wie das Produkt f₁·(-f₂).

↓

[(f₁+f₂......+f_n)/ n]² = (f₁² + f₂² + f₃² ….+ f_n²) / n²

↓

σ_M² = Mittelwert von [(f₁+f₂......+f_n)/ n]² = Mittelwert von (f₁² + f₂² + f₃² ….+ f_n²) / n² = (σ₁² + σ₂² + σ₃².....+ σ_n²)/ n²

σ_M² = σ²/n

σ² ist der Mittelwert von σ₁² , σ₂² , σ₃²...= (σ₁² + σ₂² + σ₃².....+ σ_n²) / n

σ² ist normalerweise die Varianz in Bezug auf einen Mittelwert vieler Messwerte und nicht in Bezug auf einen „wahren Wert“ , denn Letzterer ist in der Regel unbekannt. Die mittlere Fehler in Bezug auf den „wahren Wert“ soll σ und der entsprechende Fehler in Bezug auf den Mittelwert soll σ' heißen.

Kann die Differenz zwischen σ' und σ geschätzt werden ?

f sei die Abweichung eines Messwertes vom „wahren Wert“ und f' sei die Abweichung von einem aus n Messwerten gebildeten Mittelwert.

Es gilt: f = f' + d , d ist die Abweichung des Mittelwerts vom wahren Wert.

f² = (f' + d)² = f '² + 2·d·f' + d²

Für alle n Messwerte mit den Fehlern f₁, f₂ ,f₃ gilt somit:

f₁² +f₂² +f₃² +f₄²….= f '₁² +f '₂² +f '₃² +f '₄² +... 2·d·( f '₁ +f '₂ +f '₃ +f '₄......) + n·d²

Für die Abweichungen vom Mittelwert gilt: ( f '₁ +f '₂ +f '₃ +f '₄......) = 0

↓

(f₁² +f₂² +f₃² +f₄²…)/n = (f '₁² +f '₂² +f '₃² +f '₄² +... )/n + d²    →    σ² = σ'² + d²

σ²: Varianz in Bezug auf den „wahren Wert“, σ'²: Varianz in Bezug auf einen Mittelwert

Werden n Mittelwerte aus n Folgen von jeweils n Einzelwerten gebildet, dann gilt für die Folgen 1, 2, 3...:

σ₁² = σ'₁² + d₁²,   σ₂² = σ'₂² + d₂²,   σ₃² = σ'₃² + d₃²….......

Der Mittelwert von d₁², d₂², d₃²… ist die Varianz σ_M² der Mittelwerte.

↓

(Mittelwert von   σ²) = (Mittelwert von σ'² ) + σ_M², σ_M² = (Mittelwert von σ²) /n

↓

σ_M² ·n = (Mittelwert von σ'² ) + σ_M² → σ_M² ·n - σ_M² = Mittelwert von σ'² → σ_M² ·(n-1) = Mittelwert von σ'²

σ_M² = Mittelwert von σ'²/ (n-1)

Da die Varianzen der Folgen von jeweils n Messwerten bei großem n nur wenig voneinander abweichen, kann zur Berechnung von σ_M² statt des (Mittelwerts aller Varianzen σ'²) die zu einer Folge gehörende Varianz genommen werden.

σ_M² = σ'²/ (n-1)