1.9.5 Erzwungene Schwingung

Wird eine von zwei einander gegenüber stehenden Stimmgabeln gleicher Frequenz angeschlagen, dann beginnt auch die zweite Gabel zu schwingen; sie empfängt einen Ton von der ersten und tönt zurück. Man spricht in diesem Fall von Resonanz (Widerhall). Die zweite Stimmgabel wird in diesem Fall von den Kräften einer Schallwelle, die periodisch ihre Richtung wechseln, zu Schwingungen angeregt. Das Ausmaß der Anregung ist von der Frequenz des Erregers abhängig. Vermindert man die Frequenz der ersten Stimmgabel durch Anheften eines kleinen Massestücks, dann tönt nach Anschlagen dieser Gabel die zweite weit weniger stark. Mit der im folgenden beschriebenen Anordnung soll diese Abhängigkeit von der Erregerfrequenz etwas genauer untersucht werden. Ein über der Wippe aufgehängter Magnet (siehe Abb. 1) taucht in eine auf der Wippe stehende Spule, die von einem Wechselstrom durchflossen wird, dessen Frequenz von kleinen Werten an kontinuierlich ansteigt. Der Magnet wirkt mit einer periodisch wechselnden Kraft über die Spule auf die Wippe und erregt diese zum Schwingen.

Abb. 1

Hierbei wird deutlich, dass die Schwingungsamplitude dann am größten ist, wenn die Erregerfrequenz mit der Eigenfrequenz der Wippe (10Hz) übereinstimmt (siehe Abb.2). In diesem Fall sagt man, die Wippe sei in Resonanz mit dem Erreger.

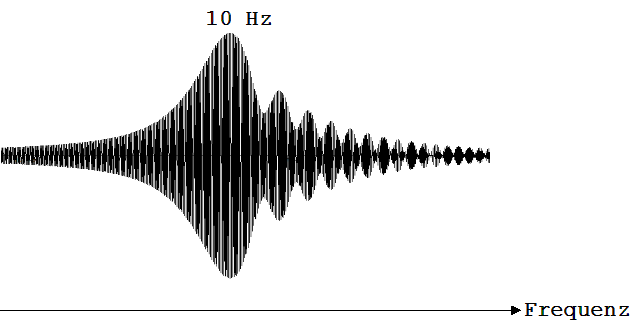
Abb. 2

Diese Resonanz wird oft als lästige Erscheinung wahrgenommen. Der Autofahrer erlebt sie manchmal als unangenehme Vibration im Fahrzeug, wenn die Reifen nicht richtig ausgewuchtet sind und infolgedessen eine Schwingung auf ein Autoteil ( z.B. das Lenkrad) übertragen, dessen Eigenfrequenz der Umlauffrequenz der Reifen gleicht.

Quantitative Untersuchung einer erzwungenen Schwingung

Zur mathematischen Behandlung der erzwungenen Schwingung stellen wir uns einen Körper der Masse m vor, der zwischen 2 Schraubenfedern mit der gemeinsamen Federkonstante D um den Nullpunkt eines Koordinatensystems entlang der y-Achse schwingt. Neben der Federkraft - D·y (die Federkraft ist der Auslenkung entgegen gerichtet) erfahre dieser Körper noch eine Kraft F = F₀ ·sin(ω·t) von außen. Somit gilt:

m ·a = - D · y + F₀ · sin(ω·t).

Wenn noch ­eine von der Geschwindigkeit abhängige Reibungskraft F_R = - k · v zu berücksichtigen ist, dann muss die Gleichung noch durch - k· v ergänzt werden.

­ m ·a = - D · y + F₀ · sin(ω·t) – k·v

Mit der folgenden Programmzeile in sim.html entsteht das Diagramm in der Abb. 3.

D=1 ; h=0,0012; m=0,01;t=t+h; r =-D*y - k*c+0,5*sin(9*t); b=r/m; b=0,5*j*(b-p)+b; y=0,5*b*h^2+c*h+y ; c=c+b*h; p=b; j=1; x=t;

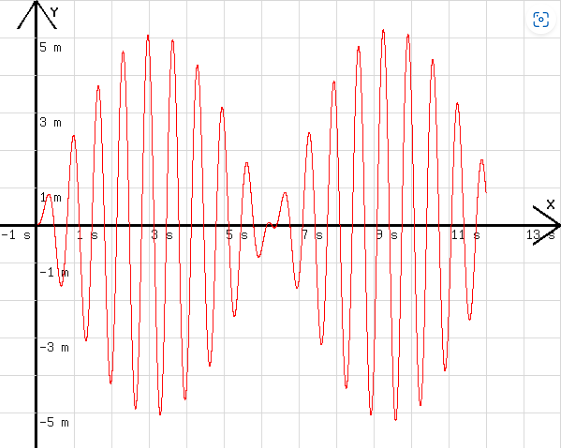
Abb. 3

Das Diagramm beschreibt die Schwingung eines Körpers mit der Eigenfrequenz ω_E = 10 s^-1 und k = 0, dessen Schwingung von einer mit ω = 9,5 s^-1 periodisch schwankenden Kraft veranlasst wird. Die Amplitudenschwankung werden im Hinblick auf die Abb.4 verständlich. In dieser Abbildung ist neben dem v-t-Diagramm des schwingenden Körpers (blau) auch noch ein schwarzes Diagramm zu sehen, welches das Fünffache der erregenden Kraft in Abhängigkeit von der Zeit darstellt. Es wird mit der folgenden Programmzeile erzeugt.

D=1 ; h=0,0012; m=0,01;t=t+h; r =-D*q - k*c +0,2*sin(9*t); b=r/m; b=0,5*j*(b-p)+b; q=0,5*b*h^2+c*h+q ; c=c+b*h; w=0,2*c; p=b; z = sin(9*t); j=1; x=t;

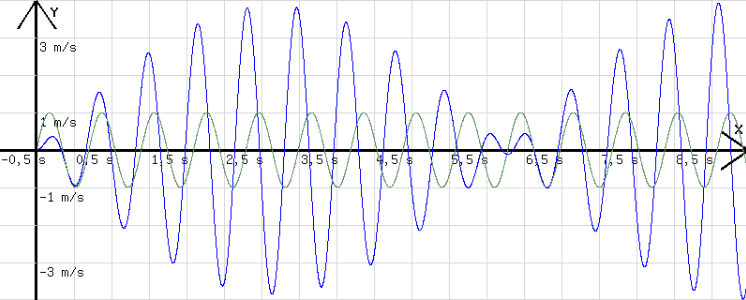
Abb.4

Zunächst hat F die Richtung von v (c), demzufolge wird der schwingende Körper fortwährend angetrieben und die Amplitude wächst. Ist das Amplitudenmaximum erreicht, dann hat die Kraft nur noch während zweier Viertelperioden die Richtung von v, folglich wird in gleichem Maß angetrieben wie abgebremst. Nach dem Maximum wird mehr abgebremst als angetrieben, weshalb die Amplitude abnimmt. Wenn die Geschwindigkeitsamplitude fast den Wert 0 erreicht hat, sind Kraft und Geschwindigkeit während der gesamten Periodendauer einander entgegen gerichtet. Hiernach erzwingt die Kraft eine Umkehr der Geschwindigkeitsrichtung (Phasensprung) und verstärkt wieder die Schwingung.

Wenn die Frequenz der erregenden Kraft gleich der Eigenfrequenz des schwingenden Körpers ist, dann wirkt die erregende Kraft immer in Bewegungsrichtung (siehe Abb.5). Die Amplitude wird bei fehlender Reibung unendlich groß.

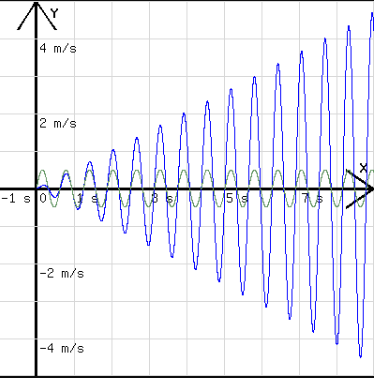
Abb. 5

Wenn Reibungskräfte im Spiel sind, dann klingt die Eigenschwingung schnell ab, und die Schwankungen der Amplitude unterbleiben (siehe Abb.6).

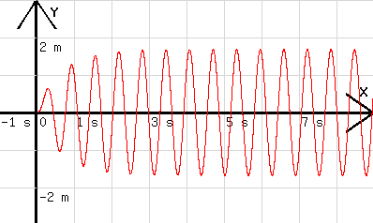
Abb. 6

Herleitung einer Formel für die Elongation einer erzwungenen Schwingung

Das Schwingungsdiagramm zu einer erzwungenen Schwingung ohne Reibung gleicht einem Schwebungsdiagramm, weshalb die folgende Summe für die Elongation y in Frage kommt.

y = A· sin(ω · t) + B· sin(ω_E ·t)

ω = Erregerkreisfrequenz, ω_E = Eigenkreisfrequenz

Die Geschwindigkeit v(0) zum Zeitpunkt t = 0 ist 0. Wie im Kapitel 1.9.1 erläutert wurde, gelten für die Geschwindigkeiten v₁ und v₂ der Schwingung y = A· sin(ω · t) und y = B· sin(ω_E ·t):

y = A· sin(ω · t); v₁ = A · ω · cos(ω ·t)

y = B· sin(ω_E ·t); v₂ = B·ω_E· cos(ω_E ·t)

↓

y = A· sin(ω · t) + B· sin(ω_E ·t); v = v₁ + v₂ = A · ω ·cos(ω ·t) + B· ω_E· cos(ω_E · t)

v(0) = 0 → A · ω = - B · ω_E → B = - A· ω /ω_E

↓

y = A· sin(ω · t) - A· (ω /ω_E) · sin(ω_E ·t) = A· [sin(ω · t) - ω · sin(ω_E ·t)/ω_E]

v = v₁ + v₂ = A· ω · cos(ω · t) -A · ω ·cos(ω_E ·t)

a = dv/dt = - A· ω² · sin(ω · t) + A · ω ·ω_E · sin(ω_E ·t)

Die Gültigkeit der letzten Gleichungen kann wie folgt geprüft werden:

y =A· [sin(ω · t) - ω · sin(ω_E ·t)/ω_E] und die zugehörende Beschleunigung a = dv/dt werden in die Gleichung m·a = - D·y + F₀ ·sin(ω·t) eingesetzt.

- m·A·ω²·sin(ω·t) + m·A·ω·ω_E·sin(ω_E·t) = -D·A·sin(ω·t) + D·A·ω· sin(ω_E ·t)/ω_E + F₀·sin(ω·t)

Die fett markierten Terme heben sich wegen D = m · ω_E² auf.

- m · A· ω² · sin(ω · t) = - D· A· sin(ω · t) + F₀ ·sin(ω·t)- m · A· ω² = - D· A + F₀ → A = F₀ /(D - m ·ω²) ; D/m = ω_E²

↓

A = (F₀/m)/ (ω_E² - ω² )

y = A·[sin(ω · t) - ω · sin(ω_E ·t)/ω_E] erfüllt mit A = (F₀/m)/ (ω_E² - ω² ) die Gleichung m·a = - D·y + F₀ ·sin(ω·t).

Der Vorzeichenwechsel von A beim Übergang ω < ω_E zu ω > ω_E deutet nicht auf einen Phasensprung hin, wie dies oft fälschlicherweise sogar in manchen Schullehrbüchern behauptet wird, denn mit A ändert auch die Differenz sin(ω · t) - ω · sin(ω_E ·t)/ω_E ihr Vorzeichen.

Wenn die Erregerfrequenz mit der Eigenfrequenz übereinstimmt (ω = ω_E), dann nimmt nach Abb. 5 die Amplitude gleichmäßig mit der Zeit zu. Das muss aus y = A·[sin(ω · t) - ω · sin(ω_E ·t)/ω_E] hervorgehen, wenn wir ω an ω_E heranrücken.

ω - ω_E = Δ ω → ω = ω_E + Δ ω

y = A·[sin(ω_E · t + Δ ω · t) - (ω_E + Δ ω) · sin(ω_E ·t)/ω_E]

y = A·[sin(ω_E · t + Δ ω · t) - sin(ω_E ·t) - Δ ω · sin(ω_E ·t)/ω_E]

A = (F₀/m)/ (ω_E² - ω² ) = (F₀/m)/ [(ω_E + ω ) ·( ω_E- ω) ]= - (F₀/m)/ [(ω_E + ω ) · Δ ω]

y = [- (F₀/m)/ (ω_E + ω ) ]· {[sin(ω_E · t + Δ ω · t) - sin(ω_E ·t) ]/ Δ ω - sin(ω_E ·t)/ω_E}

y = [- (F₀/m)/ (ω_E + ω )]·{t·[sin(ω_E · t + Δ ω · t) - sin(ω_E ·t)] / (Δ ω·t) - sin(ω_E ·t)/ω_E}

ω_E · t = u, Δ ω·t = Δu

y = [- (F₀/m)/ (ω_E + ω )]·{t·[sin(u+ Δ u) - sin(u) ]/ (Δ u) - sin(ω_E ·t)/ω_E}

Für ω → ω_E gilt : ω_E + ω → 2· ω_E

[sin(u+ Δ u) - sin(u)] / (Δ u) → cos u = cos ( ω_E· t)

y = [- (F₀/m)/ (2·ω_E )] ·{t· cos ( ω_E· t) - sin(ω_E ·t)/ω_E} = [F₀/ (2·ω_E · m)] ·{sin(ω_E ·t)/ω_E - t· cos ( ω_E· t)}

Ein Schüler, der mit der Differentialrechnung vertraut ist, kann mit der Regel von L'Hospital den hier gewonnenen Grenzwert ermitteln (nach ω differenzieren !) .

lim _{ω → ωE} [sin(ω · t) - ω · sin(ω_E ·t)/ω_E] / (ω_E² - ω² ) = lim _{ω → ωE} [t · cos (ω ·t) - sin(ω ·t)/ ω_E]/ (-2 ·ω )

Ist die Schwingung einer Schraubenfeder gedämpft, dann stellt sich bei einer erzwungenen Schwingung unter der Kraft F₀ · sin(ω·t) ein Amplitudenmaximum ein, wenn die Erregerfrequenz f gleich der Frequenz f_E = [1/(2·π)]·√(D/m) ist. f_E ist die Frequenz bei fehlender Dämpfung.

Es gilt: m·a = - D·y - k·v + F₀ ·sin(ω·t)

Nach dem Einschwingen kommt y = A·cos(ω·t) mit ω² = D/m als Lösung der Gleichung in Frage.

v = -A·ω· sin(ω·t); a = -A·ω²· cos(ω·t)

-m·A·ω²· cos(ω·t) = -D·A·cos(ω·t) + k·A·ω· sin(ω·t) + F₀ ·sin(ω·t)

Die fett gedruckten Terme heben sich wegen ω² = D/m auf.

↓

k·A·ω· sin(ω·t)+ F₀ ·sin(ω·t) = 0 → A = -F₀ /(k· ω) → y = [-F₀ /(k· ω)]·cos(ω·t)