
1.9.2 Gedämpfte Schwingung
Die Glasplatte der Wippe schwingt nach einem Stoß schnell hin und her (T = 0,1s) mit stark abklingender Amplitude (siehe Abb. 1). Wegen ihrer Amplitudenabnahme, sie erfolgt hier nach einer Exponentialfunktion, nennt man diese Schwingung gedämpft.

Abb. 1
Ebenfall stark gedämpft ist das Hin- und Herschwappen von Wasser in einer Wanne (Abb. 2) oder das Schwingen einer Wassersäule in einem U-Rohr ( Abb. 3).

Abb. 2
In der Abb. 3 ist ein U-Rohr zu sehen, welches bis zu den roten Markierungen mit Wasser gefüllt ist. Auf dem rechten Schenkel sitzt ein Stopfen, durch den ein Glasrohr hindurch geführt ist.

Abb. 3
Berechnung des vom Wasser ausgehenden Drehmoments
Wird mit einem an das Glasrohr angeschlossenen Schlauch in das U-Rohr hinein geblasen, dann stellt sich in den beiden Schenkeln ein verschieden hoher Wasserstand ein. Das Wasser schwingt, wenn der Schlauch freigegeben wird. Die Dämpfung der Schwingung kann mit einer am Schlauch angebrachten Schlauchklemme geregelt werden. Je mehr der Schlauch zusammen gequetscht wird, desto größer ist die Dämpfung. Bei sehr großer Dämpfung schwingt der Körper nicht mehr um die Ruhelage, er nähert sich ihr einseitig an (siehe Abb. 4).

Abb. 4
Ist eine solche einseitige Annäherung an die Ruhelage so, dass bei geringfügiger Verminderung der Dämpfung wieder eine gedämpfte Schwingung erkennbar ist, dann spricht man vom aperiodischen Grenzfall. Für schwingungsfähige Anzeigeteile von Messinstrumenten, zum Beispiel für den Zeiger eines Amperemeters, wird dieser aperiodische Grenzfall als Bewegungsform angestrebt, weil mit ihm die schnellste Einstellung auf den Messwert erfolgt.
Das Schwingungsverhalten eines Federpendels mit einer der Geschwindigkeit proportionalen Reibungskraft FR= -k·v kann mit dem folgenden Programm in sim.html (ist dem gegebenen Fall angepasst) etwas genauer untersucht werden.
|
D=1 ; h=0,01; m=1; K=0,5; r =-D*y - K*c; b=r/m; b=0,5*j*(b-p)+b; y=0,5*b*h^2+c*h+y ; c=c+b*h; p=b; K=2,5; r =-D*z - K*g; f=r/m; f=0,5*j*(f-q)+f; z=0,5*f*h^2+g*h+z ; g=g+f*h; q=f; K=1,7; r =-D*w - K*o; a=r/m; a=0,5*j*(a-i)+a; w=0,5*a*h^2+o*h+w ; o=o+a*h; i=a; t=t+h; x=t;j=1; l=l+1;
Für y, z und w sind die Werte 4 (4m) in das Variablenfeld einzutragen ! |
In der Abb. 5 sind Bewegungsdiagramme zu sehen, die mit diesem Programm berechnet wurden. Vorausgesetzt wurde ein 1kg schwerer Körper an einer Feder mit D = 1kg/s2, der sich unter der Kraft F = -D·y - k·v entlang der y-Achse eines Koordinatensystems bewegt. Für die Anfangswerte von y, w und z wurden die Werte 4 m in das Variablenfeld von sim.html eingetragen. Die Diagramme sind den k-Werten 0,5 kg/s (rot), 1,7 kg/s (blau) und 2,5kg/s (grün) zuzuordnen. K = 1,7 kg/s liefert den aperiodischen Grenzfall.
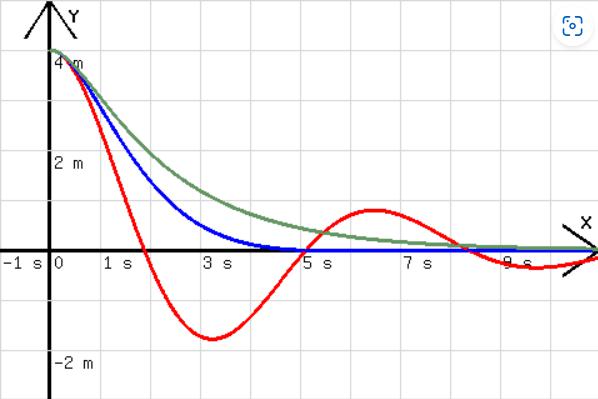
Abb. 5
Zur Berechnung dieser Diagramme ist folgendes anzumerken:
Die Bewegungszeit wird in kleine Zeitabschnitte Δt =h zerlegt. Ein Δt = h ist so klein, dass innerhalb dieses Zeitabschnitts die Kraft als konstant angesehen werden kann. Mit den für eine konstante Kraft geltenden Bewegungsgleichungen werden die Orts- und Geschwindigkeitsänderung während des ersten Zeitabschnitts h unter Berücksichtigung der für h geltenden Kraft berechnet. Nach dieser Rechnung ist der Ort und die Geschwindigkeit zu Beginn des zweiten Abschnitts der Dauer h bekannt. Die zuvor durchgeführte Rechnung wird für das neue h wiederholt usw..
1.) v2 = a·h+ v1 ; 2.) y2 = 0,5·a·h2 +v1 ·h + y1
y2 , y1: y-Werte vor und nach h
v1 , v2 : Geschwindigkeiten vor und nach h
Bei der Behandlung einer gedämpften Schwingung wird für F der Term F = - D·y - k·v gewählt. - D·y ist die zurück treibende Federkraft, - k·v beschreibt eine der Geschwindigkeit proportionale Reibungskraft FR entgegen der Bewegungsrichtung. Es wird davon ausgegangen, dass die Reibungskraft FR der Geschwindigkeit proportional ist.
|FR|/v = k (Konstante)