Schwierigkeiten in elementaren Dingen (ein Lehrerstreit)

Anlass zu der in einer 11. Klasse nicht üblichen, genauen Beschreibung der Schwerpunkteigenschaften gab ein lang anhaltender Streit um eine Schulaufgabe in einer 11. Klasse. Von einem Fachbetreuer Physik (Gymnasium) und Fachreferenten des zuständigen Kultusministeriums wurden dazu derart fachlich falsche Entscheidungen getroffen, dass es angebracht erschien, die Aufgabe in der Praxis der Naturwissenschaften unter dem Titel

„Ist der Impulssatz noch gültig ?“

vorzustellen ( Praxis der Naturwissenschaften PdN-Ph. 8/39. Jg. 1990). In diesem Aufsatz wird gezeigt, dass die genannten Personen sehr wahrscheinlich bei besserer Kenntnis der Schwerpunkteigenschaften solche elementaren Fehler nicht gemacht hätten.

Aufgabe:

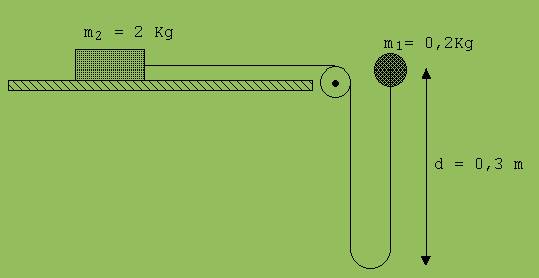
Abb. 1

Ein 2 kg schwerer Quader ( Abb. 1) liegt lose auf einer waagrechten Ebene. Ein an ihm angebundener Faden ist über eine Rolle R geführt. Der hinter der Rolle R durchhängende Faden verbindet den Quader mit einer 0,2 kg schweren Kugel in Höhe der Ebene. Wir lassen den 0,2 kg- Körper fallen.

a) Welche Geschwindigkeit haben beide Körper, wenn sich der Faden gerade gestrafft hat?

Auf den 2 kg-Körper wirkt neben dem Faden noch die waagrechte Ebene mit der Reibungskraft 10 N.

b) Welchen Weg legen beide Körper gemeinsam zurück?

Bei der Behandlung von Teil a muss der Impulssatz angewandt werden. Gegen diese Anwendung wurden überraschenderweise folgende Argumente vorgebracht:

1.) Die Anwendung des Impulssatzes ist nur dann erlaubt, wenn keine Reibungskräfte auftreten.

2.) Die Anwendung des Impulssatzes ist nur dann korrekt, wenn der Vorgang als unelastischer Stoß behandelt werden kann.

Auf Anweisung des Ministeriums wurden  falsche Lösungen zum Teil a als richtig bewertet, die mit Hilfe des Energieerhaltungssatzes berechnet wurden (kinetische Energie vor Straffung des Fadens = kinetische Energie nach Straffung des Fadens).

Behandlung der Aufgabe

Man stelle sich zunächst vor, der Körper 1 werde mit der Kraft m₁ · g nicht nach unten sondern nach rechts bewegt. Diese gedankliche Änderung ist zwar für die Behandlung der Aufgabe ohne Bedeutung, erscheint jedoch zum Verständnis des nachfolgenden Ansatzes angebracht.

Für die Änderung der Schwerpunktgeschwindigkeit ist zunächst nur die Kraft m₁·g maßgebend. Wenn sich der Faden gestrafft hat (vernachlässigbare Dehnbarkeit wird bei einem Faden vorausgesetzt), ist die Geschwindigkeit des Schwerpunkts v gleich der Geschwindigkeit des Systems aus den beiden Massen m₁ und m₂. Für die Beschleunigung  des Schwerpunkts a = v/t  während des freien Bewegung von m₁ in der Zeit t gilt :

(m₁ + m₂) · a = F;   F = m₁· g    →    (m₁ + m₂) · v/t = m₁ · g    →    (m₁ + m₂) · v = m₁· g · t

In der letzten Gleichung ist der Impulssatz zu erkennen ( v₁ = g · t ist die Geschwindigkeit von m₁ am Ende des freien Falls ).

0,6m  =  0,5 · g · t²    →     t ² = 1,2 m/9,81 m/s²       →   t = 0,35 s

v  =  0,2 kg/2,2 kg · 9,81 m/s² · 0,35 s = 0,31 m/s

Nur bei geringer Dehnbarkeit des Fadens ( sie wird normalerweise vorausgesetzt) kann der Gesamtimpuls kurz vor der Straffung des Fadens gleich dem Gesamtimpuls zu Beginn der Rutschbewegung von m₂ gesetzt werden.

Für die Weiterbehandlung der Aufgabe ist es ohne Bedeutung, ob m₁ z.B. nach der Straffung des Fadens eine geringe Hüpfbewegung macht. Wenn der Bremsklotz rutscht wirkt von nun an die Kraft F - m₁· g  (F = Gleitreibungskraft, F > m₁· g ) und bestimmt somit die Geschwindigkeitsänderung des Schwerpunktes. Auf die Bewegung dieses Punktes hat somit eine Hüpfbewegung von m₁ kurz nach seiner ungehemmten Bewegung keinen Einfluss. Das System kann so behandelt werden, als ob sich der Abstand zwischen m₁ und m₂ nicht ändert. Es sei noch angemerkt, dass der Impuls des Bremsklotzes (nicht der Gesamtimpuls) nach dem Impulssatz größer wird, wenn m₁ hoch hüpft.

Für die Zeit t₂ der gemeinsamen Bewegung gilt somit:

(m₁+m₂)·v/t₂ = F - m₁· g       →       t₂ = (m₁+m₂) · v/(F- m₁· g)

und für den gemeinsamen Weg : s = t₂ · 0,5 · v      (0,5 · v = mittlere Geschwindigkeit)

Es handelt sich um eine gleichförmig-beschleunigte Bewegung, die mittlere Geschwindigkeit ist deshalb der Mittelwert aus der Anfangsgeschwindigkeit v und Endgeschwindigkeit 0.

t₂ = ( 2,2 kg · 0,31 m/s) / (10 N - 0,2 kg · 9,81 m/s²) = 0,08 s

s = 0,08 s · 0,5 · 0,31 m/s = 12 mm

Experimentelle Behandlung

Zur experimentellen Untersuchung des beschriebenen Sachverhalts ist die Experimentierwippe besonders gut geeignet, da mit ihr Schwerpunktsbewegungen registriert werden können. Zunächst wird der Impulssatz in einer Weise demonstriert, die der geschilderten Aufgabe entspricht. Auf der Wippe sind zwei Experimentierwagen zu sehen (Abb. 2) , die mit einem Faden verbunden sind. Wenn der vordere Wagen angestoßen wird, dann bewegt sich der hintere Wagen etwas später nach Straffung des Fadens. Trotz dieser Wechselwirkung zeichnet der Rechner ein lineares Diagramm (Abb. 3) zur Schwerpunktsbewegung. Selbstverständlich muss vor diesem Experiment ein Reibungsausgleich in Bewegungsrichtung vorgenommen werden.

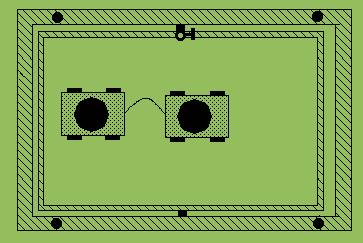
Abb. 2

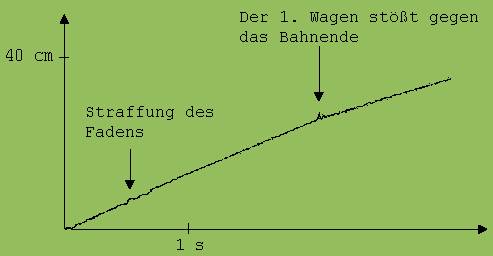
Abb. 3

Das Diagramm der Abb. 4 beschreibt die Bewegung eines Bremsklotzes, der wie in Abb. 1 sichtbar von einem zunächst fallenden Zuggewicht über die Wippe gezogen wird.

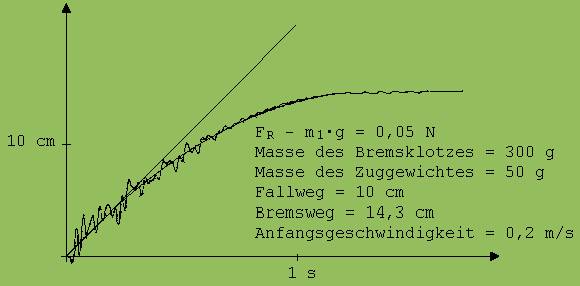
Abb. 4

An diesem Diagramm (gute Reproduzierbarkeit) kann die Übereinstimmung von Theorie und Praxis gezeigt werden. Die Abweichungen sind erstaunlich gering. Die eingezeichnete Parabel beschreibt die Bewegung des Bremsklotzes unter der Kraft F_R - m₁·g = 0,05 N (Reibungskraft - Gewichtskraft von m₁). Die Steigung der eingezeichneten Tangente gleicht der Geschwindigkeit nach Straffung des Fadens (Anfangsgeschwindigkeit des Bremsklotzes). Die Schwankungen des Diagramms beruhen auf Schwingungen der Glasplatte. Die plötzlich am Bremsklotz angreifende Kraft ist für ein Drehmoment verantwortlich, welches der Wippe mitgeteilt wird und diese zu Schwingungen anregt. Dieses Drehmoment ist um so größer, je höher der Faden oberhalb der Gleitfläche am Bremsklotz angebunden ist.