1.3.7 Momentangeschwindigkeit und Beschleunigung

Bei dem in 1.3.6  dargestellten Experiment wurde zum Zeitpunkt 2,2 s der Luftstrom vom Experimentierwagen weg gelenkt, damit dann an einer gleichförmigen Bewegung die Geschwindigkeit v zu diesem Zeitpunkt bestimmt werden kann.

Kann man an einem s-t- Diagramm die Geschwindigkeit zu einem bestimmten Zeitpunkt t auch auf andere Weise bestimmen ?

Folgendes Vorgehen erscheint angemessen. Es wird die Strecke Δs bestimmt, die während eines kurzen, auf den Zeitpunkt t folgenden Zeitabschnitts Δt zurückgelegt wird. Δt wird so klein gewählt, dass sich in dieser kurzen Zeit die Kraft nur wenig auf die Bewegung auswirken kann, weshalb Δs/Δt kaum von der Geschwindigkeit v abweicht, die sich einstellt, wenn nach t keine Kraft wirkt. Die Abweichung |Δs/Δt – v| strebt mit kleiner werdendem Δt gegen 0. Man sagt in diesem Fall, v ist der Grenzwert von Δs/Δt für Δt → 0.

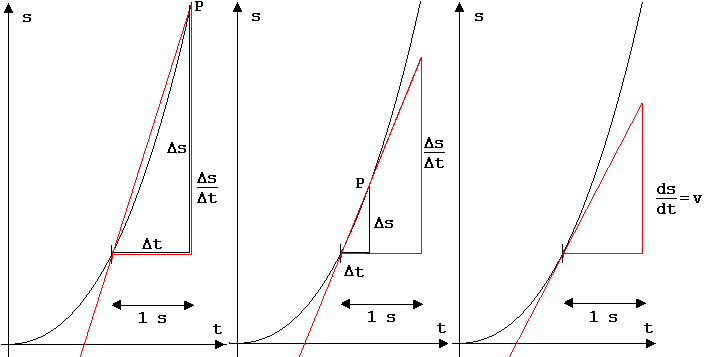
An der Bilderserie in Abb. 1 ist die Entwicklung zu dem genannten Grenzwert v zu erkennen. Durch Anfang und Ende von Kurvenabschnitten, die in Zeitintervallen Δt unmittelbar nach dem Zeitpunkt t = 1 s entstehen, werden Geraden gelegt. Die Steigung einer Geraden ist gleich dem Quotienten Δs/Δt. Mit kleiner werdendem Δt streben die Geraden gegen eine Grenzlage. Eine Gerade in dieser Grenzlage wird Tangente (Berührungsgerade) genannt. Ihre Steigung ist gleich der Momentangeschwindigkeit v. Für den Grenzwert von Δs/Δt schreibt man lim Δs/Δt_{( Δt → 0)} oder ds/dt ( sprich ds nach dt). Mit der Sprechweise „ds nach dt“ anstelle von „ds durch dt“ soll vermieden werden, dass dieser Grenzwert (Differentialquotient) als Quotient bestimmter endlicher Größen aufgefasst wird. Lim ist eine Abkürzung für Limes (Grenze).

Abb.1

Vorführung

Als Momentangeschwindigkeit v zu einem bestimmten Zeitpunkt t wir der Grenzwert von Δs/Δt definiert.

v = lim Δs/Δt_{( Δt → 0)}

lim Δs/Δt_{( Δt → 0)} = ds/dt

v = ds/dt

Zu einer Bewegung nach s = ½ ·a ·t² kann die Momentangeschwindigkeit in Abhängigkeit von der Zeit t berechnet werden.

Nach s = ½·a · t² gilt für die mittlere Geschwindigkeit v_m in einem Zeitabschnitt zwischen den Zeiten t und t' (t < t' ) :

Δs = ( ½ ·a · t'² - ½ ·a · t²), Δt = (t' – t), v_m = Δs / Δt

v_m = ( ½ ·a · t'² - ½ ·a · t²) / (t' – t) = ½ ·a ·(t'² - t²) / (t' – t) = ½ ·a ·(t' + t )

(t'² - t²) = (t' + t )·(t' – t) !

Unter einer mittleren Geschwindigkeit v_m = s/t verstehen wir das Verhältnis aus einem zurückgelegten Weg s und der zugehörenden Zeit t. Diese Definition ist an keinen besonderen Bewegungsablauf geknüpft; die Bewegung kann in der Zeit t langsamer oder schneller werden. Lässt man t' schrittweise näher an t heranrücken, somit Δt immer kleiner werden, dann strebt v_m = Δs/Δt gegen den Wert ½ ·a ·(t + t ) = a · t

v (Momentangeschwindigkeit zum Zeitpunkt t ) = ds/dt = lim Δs/Δt_{( Δt → 0)} = a · t

Nach v_m = ½ ·a ·(t' + t ) = ½ · (a ·t' + a · t ) ist die mittlere Geschwindigkeit in einem Zeitabschnitt gleich dem Mittelwert aus der End- und Anfangsgeschwindigkeit v_t' = a ·t' und v_t = a ·t'.

Hier ist anzumerken, dass der Satz „Die mittlere Geschwindigkeit ist der Mittelwert aus der Anfangs- und Endgeschwindigkeit“ nur bei einer gleichförmig - beschleunigten Bewegung gilt.

Es stellt sich nun die Frage, welche der uns bekannten Bewegungen als gleichförmig-beschleunigt anzusehen sind. In Frage kommt z.B. die Fallbewegung eines Körpers. Wir werden diese Bewegung daraufhin untersuchen.

 Untersuchung einer gleichförmig-beschleunigten Bewegung mit der vorliegenden On-Line-Stoppuhr

2. Der Freie Fall (Gewichtskraft)

Aufgaben