
1.3.6 Definition der Kraft und des Kraftmaßes
Da in einem abgeschlossenen System die Summe aus den Impulsen der Systemteile konstant ist, können wir eine Impulsänderung immer auf eine äußere Einwirkung, eine Kraft, zurückführen.
Erfährt ein Gegenstand A unter Einwirkung eines Gebildes B eine Impulsänderung, wenn keine Bewegungshemmnisse vorhanden sind, dann sagt man, B übe eine Kraft F (Force) auf A aus.
Wenn der Impulssatz nicht gelten würde, dann wäre selbst bei einem einzigen Teilchen eine Impulsänderung nicht als Zeichen einer äußeren Einwirkung zu deuten. Die Summe aus den Impulsen seiner Atome könnte schwanken, was nicht ohne Einfluss auf die Teilchengeschwindigkeit bliebe.
Die Wirkung auf A kann durch eine ihr entgegengesetzte Einwirkung aufgehoben werden. Man denke an zwei gedehnte Schraubenfedern, die von links und rechts an A angreifen. Auch wenn unter diesen Umständen keine Impulsänderung stattfindet, sondern eine solche nur ohne Gegenwirkung zu erwarten ist, spricht man von einer von B ausgehenden Kraft . Es ist demnach angebracht, die Kraft wie folgt zu definieren:
Unter einer Kraft versteht man die Fähigkeit eines Gebildes, den Impuls eines Körpers zu ändern.
Wie wird ein beweglicher Gegenstand unter einer gleichbleibenden Kraft angetrieben ? Eine Antwort dazu finden wir mit dem folgenden Experiment.

Abb. 1

Abb. 2
Auf der ebenen Glasplatte der Wippe wird ein Experimentierwagen vom Luftstrom eines dem Wagen nachgeführten Föhns angetrieben. Die Impulsänderung des Wagens ist der Zeit des Anblasens proportional, denn die aus dem Föhn strömende Luft erfährt am Wagen in gleichen Zeiten Δt gleiche Impulsänderungen entgegen der Fahrtrichtung, welche nach dem Impulssatz dem Betrage nach gleiche Impulsänderungen des Wagens in Fahrtrichtung zur Folge haben.
Demnach ist der Impuls m· v und somit auch die Geschwindigkeit v des Wagens der Zeit t des Anblasens proportional. Das konstante Verhältnis v/t wird Beschleunigung a genannt.
Die Beschleunigung a beschreibt die Geschwindigkeitszunahme in einer Zeiteinheit, wenn a konstant bleibt oder bliebe.
v / t = a → v = a·t
Da mit der Experimentierwippe kein v-t-Diagramm, sondern nur ein Weg-Zeit-Diagramm aufgenommen werden kann, stellt sich folgende Frage: Wie ist ein Weg-Zeit-Diagramm beschaffen, wenn v = a · t gilt? Anhand eines beliebig gewählten linearen v-t-Diagramms nach v = a·t (siehe roter Graph in der Abb. 2) kann gezeigt werden, wie der zurückgelegte Weg s in Abhängigkeit von der Zeit t bestimmt werden kann.
Die Beschleunigungszeit t ist in viele kleine Zeitabschnitte gleicher Größe Δt eingeteilt. Die Wegänderung Δs in einem solchen Abschnitt erhält man mit Δs = v' · Δt. v' ist die Geschwindigkeit in der Mitte von Δt. Wenn im Diagramm zur Darstellung von 1 s und 1m/s jeweils 1cm gewählt wird, dann stimmt Δs = v'· Δt zahlenmäßig mit dem Flächeninhalt des über Δt sichtbaren Rechtecks überein und der gesamte Weg s, die Summe aller Δs, wird durch den Flächeninhalt des Dreiecks unter dem v-t-Diagramm beschrieben.
s = (a·t) ·t / 2 = ½ · a ·t2
In der Abb. 3 ist ein s-t-Diagramm zu sehen, welches während des in der Abb. 1 dargestellten Experiments aufgenommen wurde. 2,2 Sekunden nach Beginn der Bewegung wurde der Föhn vom Wagen abgedreht. Die Bewegung wurde daraufhin gleichförmig, was an der linearen Fortsetzung des s-t-Diagramms erkennbar ist. An dem linearen Teil des Diagramms kann Geschwindigkeit 0,164 m/s zum Zeitpunkt 2,2 s bestimmt werden.

Abb.3
Die Beschleunigung a ist demnach (0,164 m/s) / 2,2s = 0,074 m/s2. Der Kurvenverlauf innerhalb der ersten 2,2 s wird genau durch die Funktion s = ½ · (0,074 m/s2) · t2 beschrieben. Somit ist bestätigt, dass während des in der Abb. 1 gezeigten Versuchs die Geschwindigkeit der Zeit proportional zunimmt. Man spricht in einem solchen Fall von einer gleichförmig - beschleunigten Bewegung.
Der Wagen mit der Masse 461g hat nach 2,2s den Impuls 0,461 kg·0,164m/s = 0,076 kg ·m/s.
Wenn es um ein geeignetes Maß für die Stärke des Luftstroms geht, dann muss man feststellen, dass die Impulsänderung in Richtung des Luftstroms allein als Maß für die Stärke des Luftstroms ungeeignet ist, denn bei schwachem Strom erreicht der Experimentierwagen auch eine große Impulsänderung, wenn man sich genügend Zeit lässt. Je kürzer die Zeit Δt für ein bestimmtes Δ(m· v) ist, desto stärker ist der Luftstrom. Δ(m· v) / Δt erscheint somit als passendes Maß für die Kraft F. Während des hier beschriebenen Experiments wirkte die Kraft F = (0,076 kg ·m/s ) / 2,2s = 0,034 kg ·m/s2 . Die Einheit kg · m/s2 wird Newton (Abkürzung: N) genannt. Mit dem Anhängsel kg · m/s² (Einheit der Kraft) wird zum Ausdruck gebracht, wie und in welchen Einheiten die zugehörigen Größen verrechnet werden. Der Leser sollte nicht versuchen, diese Einheit zu veranschaulichen, wie dies zum Beispiel bei den Grundeinheiten Meter oder Kilogramm möglich ist.
Wenn Δ(m· v) / Δt konstant ist, dann ist die Impulsänderung der Beschleunigungszeit proportional. Man kann deshalb sagen: F =Δ(m· v) / Δt steht für die Änderung des Impulses während einer Zeiteinheit unter der Voraussetzung, dass Δ(m· v) / Δt in dieser Zeit konstant gehalten wird.
Nach Einführung des Kraftmaßes ist man geneigt, nach den Kräften zu fragen, die von verschiedenen Dingen z.B. von gedehnten Schraubenfedern (Gummifäden) ausgehen. In Abb. 4 ist dargestellt, wie man entsprechend der Definition des Kraftmaßes die Kraft einer gedehnten Schraubenfeder oder eines gedehnten Gummifadens ermitteln kann.

Abb.4
Ein auf der Wippe stehender Experimentierwagen W der Masse m ist mit einer langen von 0,2 m auf 0,7m gedehnten Schraubenfeder (Gummifaden) verbunden. Mit Hilfe des Zugfadens Z wird der Wagen ein wenig nach links gezogen und danach losgelassen. Ein Faden Fa, der beiderseits am äußeren Rahmen der Wippe befestigt ist, schränkt die Bewegungsfreiheit der Feder auf etwa 5 cm ein. Unter Einwirkung der Schraubenfeder (Gummifaden) schnellt der Wagen nach rechts (an den Reibungsausgleich denken). Der Rechner zeichnet hierbei ein s-t-Diagramm zur Bewegung des Wagens W. Der Punkt A dieses Diagramms kennzeichnet den Anfangszustand. Bei B wird der Wagen freigegeben. Bei C ist die Feder wieder in ihrer Anfangslage; die Schraubenfeder (Gummifaden) wird dann von dem gespannten Faden Fa gehalten und wirkt deshalb nicht mehr auf den Wagen ein. Der sich an C anschließende Teil des Diagramms beschreibt eine gleichförmige Bewegung. Aus seiner Steigung kann die Endgeschwindigkeit Δv des Wagens (Geschwindigkeitsänderung des Wagens nach seiner Freigabe) bestimmt werden. Die Wirkungszeit Δt der Schraubenfeder (Beschleunigungszeit) ist gleich dem zeitlichen Abstand der Punkte B und C. Anhand der am Diagramm ablesbaren Werte erhält man für die Kraft: F = (0,45 kg · 0,2 m/s) /0,34s = 0,26 N.
Folgendes ist zu beachten: Die Masse der Schraubenfeder sollte im Vergleich zur Wagenmasse vernachlässigbar klein sein. Andernfalls hätte auch die Masse der Feder einen messbaren Einfluss auf die Impulsänderung des Wagens. Gummifäden eignen sich für diesen Versuch besser als Schraubenfedern.
In der nächsten Abb. 5 ist ein in der Zeit Δt von A nach B fliegender Körper K der Masse m zu sehen, der von der Seite her angeweht wird. Hierbei ändert K seine Geschwindigkeit v' sowie seinen Impuls m· v' in Windrichtung nicht aber seine Geschwindigkeit v'' quer zu ihr. Unter der Geschwindigkeit von K in einer bestimmten Richtung ist die Geschwindigkeit der rechtwinkligen Projektion K' bzw. K'' von K auf eine in diese Richtung weisende Strecke zu verstehen. Für die Kraft F gilt in diesem Fall: F = Δ(m· v' ) / Δt .
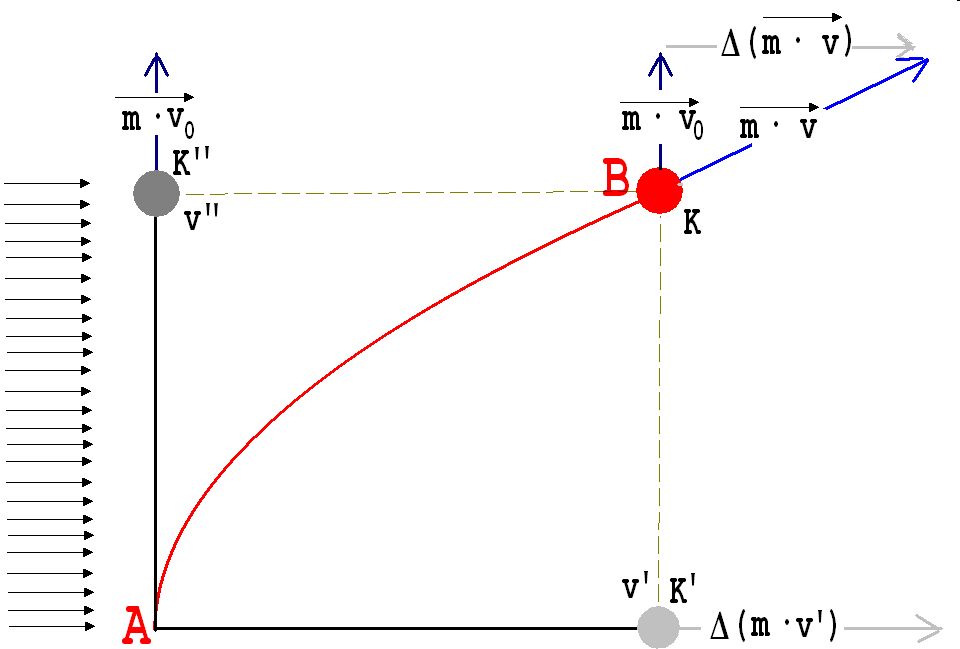
Abb. 5
Δ(m· v' ) ist dem Betrage nach gleich Δ (m · v) = m · v - m · v0. Der als Kraftvektor bezeichnete Quotient Δ (m · v)/ Δt beschreibt die Kraft nach Richtung und Größe.
Wenn die Masse m sich nicht ändert, dann kann für F geschrieben werden: F = m · Δ v/ Δt, Δ v/ Δt = a → F = m · a.
Δ v/ Δt heißt Beschleunigungsvektor a. Er zeigt in die Richtung, in der K beschleunigt wird und gibt mit seinem Betrag die Beschleunigung a an, die K in dieser Richtung erfährt.