Warum wählen wir die Namen sinh(x) und cosh(x)?

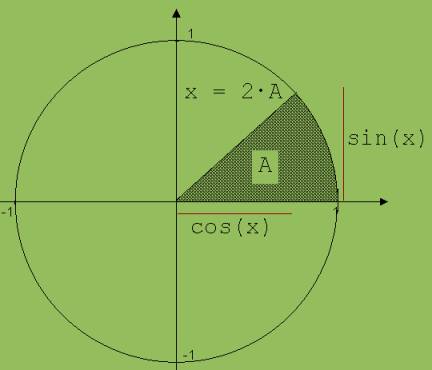
 Abb. 1

In der Abb. 1 ist die Bedeutung von sin(x) und cos(x) veranschaulicht.

x ist der zum Sektor mit dem Flächeninhalt A gehörende Winkel im Bogenmaß.

Für A gilt: A = x ·  Längeneinheit² / 2

→  x = 2·A / Längeneinheit²

Die Variable x in sin(x) und cos(x) kann demnach auch über den Flächeninhalt des Sektors definiert werden.

Zu dieser Definition muss noch vereinbart werden, dass A bei einer Linksdrehung positiv und bei einer Rechtsdrehung negativ gewertet wird.

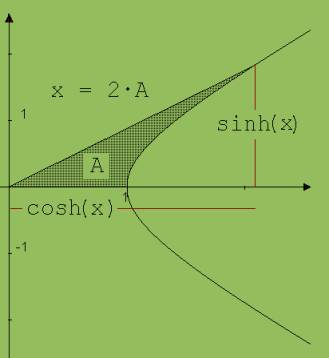
 Abb. 2

In der Abb. 2 ist die Bedeutung von sinh(x) und cosh(x) veranschaulicht.

Hier wird A nicht durch einen Einheitskreis, sondern durch die Hyperbel  x² - y² =1 begrenzt.

x = 2·A/ Längeneinheit²