1.    Keplersches Gesetz

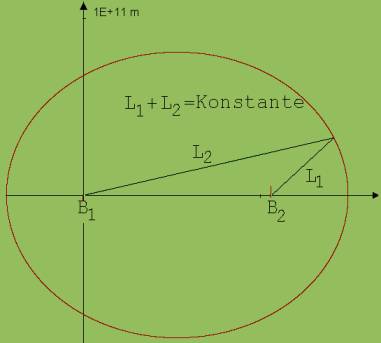
Abb. 1

Die Planeten bewegen sich auf Ellipsen um die Sonne, welche in einem Brennpunkt der Ellipse steht.

Das besondere Wesensmerkmal einer Ellipse ist in Abb. 1 angedeutet.

Zu einer Ellipse gibt es zwei Punkte B₁ und B₂, deren Abstände L₂ (r) und L₁ (L) zu einem gegebenen Ellipsenpunkt P eine von der Wahl dieses Punktes unabhängige, konstante Summe ergeben.  

Vorführung

Die genannte Summe ist gleich der Breite 2·a der Ellipse. B₁ (Sonne) und B₂ werden Brennpunkte genannt. Das 1. Keplersche Gesetz kann mit dem folgenden Programm in sim.html überprüft werden.

Beachte: In dem genannten Programm steht r für L₂ und L für L₁ !

Neben der Planetenbahn wird eine waagrechte Strecke angezeigt. Es ist das Diagramm zu w=(r+L)/2 = (r+wrz(y^2+(x-8,3E10)^2))/2, dessen waagrechter Verlauf die Richtigkeit des ersten Keplerschen Gesetzes anzeigt. 8,3E10 m ist der Abstand des zweiten Brennpunkts B₂ vom Nullpunkt des Koordinatensystems. B₁ und B₂ sind von der Mitte der Ellipse gleich weit entfernt.

h=800; m=2E30; G=6,67E-11; R = wrz(x*x+y*y);i=G*M/R^3; a=-i*x; b=-i*y; a=0,5*j*(a-o)+a;b=0,5*j*(b-p)+b; x=0,5*a*h^2+c*h+x;

y=0,5*b*h^2+d*h+y ; c=c+a*h; d=d+b*h; o=a;p=b; j=1; w=(r+wrz(y^2+(x-8,3E10)^2))/2;t=t+h

Anfangswerte von x =1E11 m und d= v_y =20000 m/s

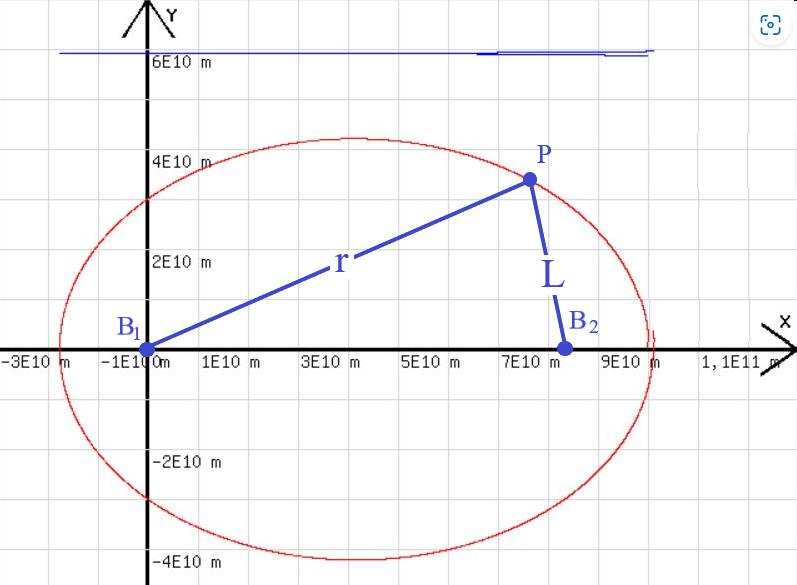
Abb.1

Anmerkung zum Begriff „Brennpunkt“:

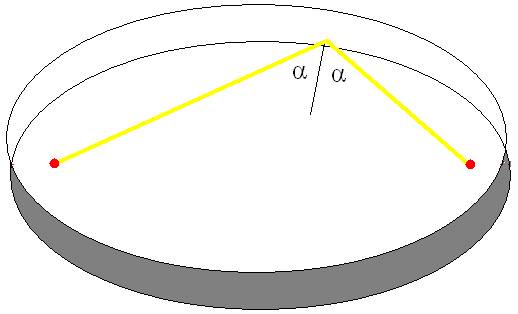
Abb. 2

Ein spiegelndes Band auf einer Ellipse ( siehe Abb. 2) reflektiert einen Lichtstrahl, der von einem Brennpunkt ausgeht, zu einem anderen Brennpunkt.