Die Flächengeschwindigkeit
(das Vektorkreuzprodukt )
Das 2. Keplersche Gesetz gilt nicht nur für
Planeten in Bezug auf die Sonne, sondern für jeden Körper
K, der sich unter einer Kraft bewegt, die auf ein bestimmtes Zentrum
gerichtet ist. Man spricht in diesem Fall von einer Zentralkraft. Zur
Prüfung dieser Behauptung muss eine Gleichung zur Berechnung der
Flächengeschwindigkeit hergeleitet werden. Unter dieser
Flächengeschwindigkeit vA verstehen wir das
Verhältnis A/Δt.
A ist die Fläche, welche in der Zeit Δt von der
Verbindungsstrecke Körper-Zentrum (Länge = r) überstrichen
wird. In der Abb.1 ist die Bewegung (rot)
während eines kleinen Zeitabschnitts Δt
dargestellt.
|
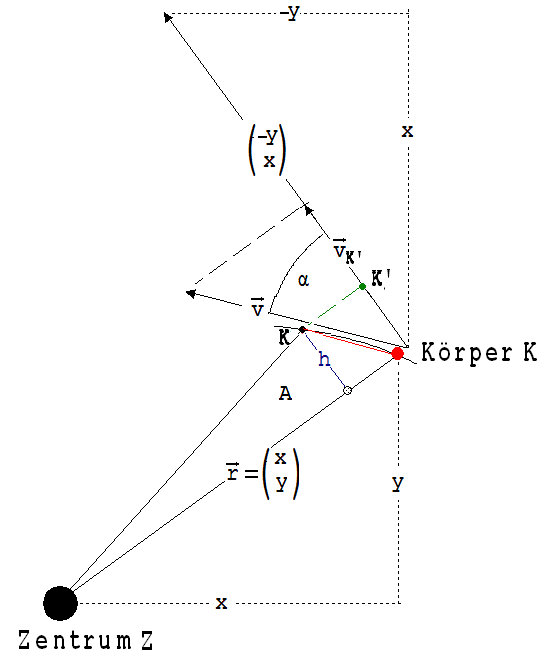
Abb. 1
|
A
= ½ ·h ·|r|
; vA
=
A / Δt = ½·(h /Δt) ·|r|
(h
/ Δt) = |vK'|
ist die Geschwindigkeit von Kʼ, der Projektion von K auf den
Vektor {-y,x}. {-y,x} bildet mit r
einen
rechten Winkel.
vA
=
A/ Δt = 0,5·|vK'|
·|r|
Da
{-y,x} den gleichen Betrag wie r
hat,
können wir |r|
durch |{-y,x}| ersetzen.
vA
=
½ ·|vK'|
·|{-y,x}|; |vK'
|
=
|v|·cos
(α)
vA
=
|v|
· |{-y,x}| · cos (α)
|v|
· |{-y,x}| · cos (α) = v·
{-y,x} = -v1·
y + v2
·
x
Skalarprodukt !
|
Behauptung:
vA
ist
konstant.
Beweis: dvA/dt
= 0,5 ·
[- (dv1/dt)
·
y - v1
·
dy/dt + (dv2/dt)·
x + v2
·
dx/dt]
Produktregel
der Differentialrechnung !
dx / dt = v1,
dy / dt = v2 , dv2 / dt = a2 , dv1
/ dt = a1
dvA/dt
= 0,5 · (-a1
·
y - v1
·v2
+
a2
·
x + v2
·
v1)
= 0,5 · (-a1
·
y + a2·x
)
dvA/dt
= 0,5 · {a1
,
a2
}
· {-y, x}, {a1
,
a2
}
┴
{-y,
x} → {a1
,
a2
}
· {-y, x} = 0 → dvA/dt
= 0
Demnach
ist vA
während
einer Bewegung unter einer Zentralkraft konstant. Das zweite
Keplersche Gesetz ist somit bewiesen.
Vektor der
Flächengeschwindigkeit
Der
Flächengeschwindigkeit ordnen wir einen Vektor vA
mit
|vA|
= vA
zu,
der mit seiner Richtung die Orientierung der Ebene E anzeigt, in der
sich r
dreht.
vA
steht
definitionsgemäß so senkrecht auf E, dass ein Betrachter
mit Blick auf seine Vektorspitze den rotierenden Körper K
in
einer
Linksdrehung (positive Drehung) sieht (siehe Abb.2).
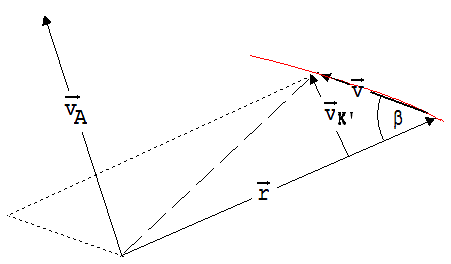
Abb.2
{0;
0; 0,5· (x ·v2
-
y·v1)}
ist vA
bei
einer Bewegung in der x-y-Eben.
{0;
0,5·(-x ·v3
+
z·
v1)
;0} ist vA
bei
einer Bewegung in der x-z-Ebene.
{0,5·
(y ·v3
-z
· v2);
0; 0} ist vA
bei
einer Bewegung in der y-z-Ebene.
Behauptung:
vA
=0,5·
{ (y ·v3
-
z · v2
)
; (-x ·v3
+
z· v1
);
(x ·v2
-y·v1)
}
gilt allgemein.
Beweis:
1.
Die
Skalarprodukte
von { (y ·v3
-
z · v2
)
; (-x ·v3
+
z· v1
);
(x ·v2
-y·v1)
}
mit
r
und
v
sind
Nullvektoren.
Folglich
steht der Vektor 0,5· { (y ·v3
-
z · v2
)
; (-x ·v3
+
z· v1
);
(x ·v2
-y·v1)
}
senkrecht auf der von r und v aufgespannten Ebene .
2.
|{ (y ·v3
-
z · v2
)
; (-x ·v3
+
z· v1
);
(x ·v2
-y·v1)
}|2
=
(y ·v3
-
z · v2
)2
+
(-x ·v3
+
z· v1
)2
+
(x ·v2
-y·v1)2
ist
gleich der doppelten Flächengeschwindigkeit.
(2·vA)2
=
(|vKʼ|
· |r|)2
(siehe
Abb.2 )
(|vKʼ|
· |r|)2
= (|v|
· sin(β) · |r|
)2
= |v|2
· |r|2
· sin2(β)
sin2(β)
= [1 - cos2(β)
], |-r| = |r|
|v|2
· |r|2 ·
sin2(β)
= v2 · r2 -
[|v| · |-r| ·
cos(β)] 2
|v|
· |-r| ·
cos(β) = v
·
(-r
)
(2·vA)2
=
v2
·
r2
-
[v
·
(-r
)]2,
[v
·
(-r
)]2
=
[v
·
r]2
↓
(2·vA)2
=
v2
·
r2
-
[v
·
r]2
Die Gleichheit von
(2·vA)
2
=
(v12
+
v22
+
v32
) ·
(x2
+ y2
+ z2
) –
(x· v1
+ y·
v2
+ z·
v3
) 2
und (y·
v3–
z · v2
) 2
+ (z· v1–
x · v3
) 2
+ ( x· v2-
y · v1
) 2
erkennt man nach
Ausmultiplikation beider Terme.
Kreuzprodukt
{
y· v3
– z
· v2
;
z· v1
– x
· v3
;
x· v2
-
y · v1
}
wird Kreuzprodukt
r x
v
aus
den Vektoren r
und
v
genannt.
Diese Bezeichnung
verdankt der angegebene Vektor der nun folgenden Regel zur
Berechnung seiner Koordinaten.
Die Koordinaten der
beiden Vektoren r
und v
werden nebeneinander in Säulen
angeordnet.
x
|
v1
|
Zur
Berechnung der x - Koordinate wird diese 1. Zeile gestrichen
|
y
|
v2
|
Zur
Berechnung der y Koordinate wird diese 2. Zeile gestrichen
|
z
|
v3
|
Zur
Berechnung der z Koordinate wird diese 3. Zeile gestrichen
|
Zur
Berechnung der n. Koordinate von r
x
v
wird die n. Zeile gestrichen. Anschließend wird der erste Wert
der verkürzten 1. Spalte mit dem zweiten Wert der anderen Spalte
und hiernach der zweite Wert der ersten mit dem ersten Wert der
zweiten Spalte multipliziert. Schließlich wird das zweite
Produkt vom ersten subtrahiert. Bei
Berechnung der y-Koordinate ist dann noch das Vorzeichen der
Differenz umzukehren.
Es
muss angemerkt werden, dass Kreuzprodukte nicht nur aus Orts- und
Geschwindigkeitsvektoren, sondern aus vielerlei Vektoren a
und
b
gebildet
wird.
a
x
b
= {
a2·
b3
– a3
·
b2;
a3·
b1
– a1
·
b3;
a1·
b2
– a2
·
b1
}
a,
b und
a x
b
verhalten
sich der Richtung nach wie der Daumen, der Zeige- und der
Mittelfinger der rechten Hand, wenn der Mittelfinger von den beiden
anderen rechtwinklig abgespreizt ist (
Rechte-Hand-Regel ).
|a
x
b|
ist gleich dem Flächeninhalt des von
a
und
b
aufgespannten
Parallelogramms, wenn als Flächeneinheit ein Rechteck gewählt
wird mit der Einheit von a
als
Länge und der Einheit von b
als
Breite.

Abb. 3


