1. Kugelvolumen
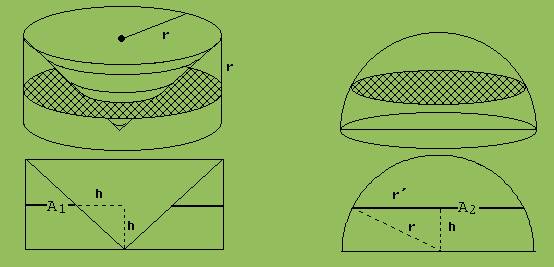
Nach Anklicken dieser Zeile sehen wir einen Zylinder mit einer kegelförmigen Bohrung und eine Halbkugel. Beide Körper stimmen in der Grundfläche und der Höhe überein und haben nach dem Prinzip des Cavalieri gleiche Volumina.

Abb. 1
A1: Inhalt der Ringfläche in der Höhe h A2: Inhalt der Kreisfläche in der Höhe h
A1 = π · r2 - π· h2 = π · ( r2 – h2) A2 = π · r’2 = π · ( r2 – h2 )
→ A1 = A2
Nach Cavalieri habe beide Körper gleiche Volumina. Für das Volumen V des Zylinders mit kegelförmiger Bohrung gilt:
V = π · r2 · r – 1/3 · π · r2 · r = 2/3 · π · r3 ( Höhe des Zylinders = r)
V gleicht dem Volumen einer Halbkugel mit dem Radius r.
Für das Volumen VK der Vollkugel gilt demnach: VK = 4/3 · π· r3
2. Volumen eines Kugelsegments
Wird eine Kugel durch einen ebenen Schnitt in zwei Kugelsegmente geteilt (siehe Abb. 2).
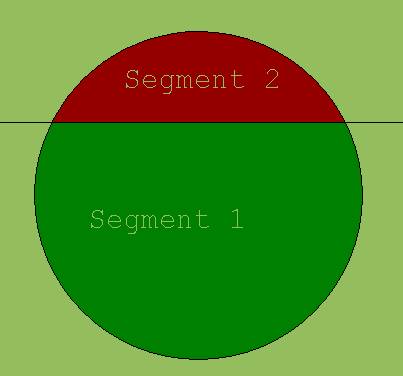
Abb. 2
Nach dem Prinzip des Cavalieri erhält man einen Körper mit dem Volumen des oberen Segments, wenn man aus einem Zylinder mit dem Radius r und der Höhe h einen Kegelstumpf herausdreht (siehe Abb. 3).
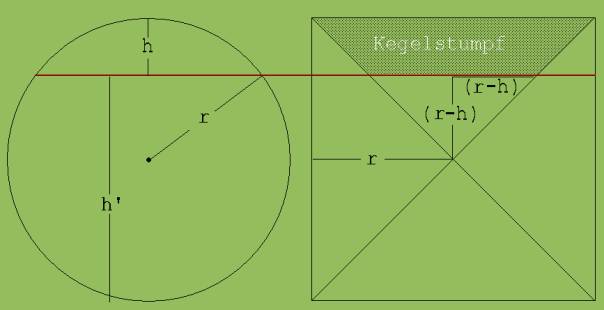
Abb. 3
Volumen VSt des Kegelstumpfs:
VSt = 1/3 ·π · r2
· r – 1/3 ·π · (r-h)2
· (r-h) = 1/3 ·π · r3 -1/3 ·π
· (r3 –h3 – 3 · r2
· h + 3·r · h2)
Volumen des Kegels mit der Höhe r – Volumen des Kegels mit der Höhe r – h !
VSt = π · (1/3 · h3 + r2 · h - r · h2)
Volumen VSegment :
VSegment = π · r2 · h - π · (1/3 · h3 + r2 · h - r · h2) = π · (r · h2 - 1/3 · h3 )
Soll das untere Segment berechnet werden, dann muss h durch h’ ersetzt werden.