|
|
|
|
Abb. 1 |
Abb. 2 |
Prüfung der Planetenbahn auf Ellipsenform mit Hilfe einer Gleichung für die x- und y-Koordinaten der Ellipse
Der Ellipse wird ein Koordinatensystem zugeordnet. Die x –Achse läuft durch die beiden Brennpunkte, die y-Achse halbiert die Verbindungsstrecke der Brennpunkte rechtwinklig. Die halbe Abstand der Brennpunkte von einander wird Exzentrizität e genannt. Mit a und b werden die halben Ellipsendurchmesser auf der x- und y-Achse bezeichnet.
|
|
|
|
Abb. 1 |
Abb. 2 |
L1 = [(x-e)2 + y2 ] ½ ; L2 = [(x+e)2 + y2 ] ½ → [(x-e)2 + y2 ] ½ + [(x+e)2 + y2 ] ½ = Konstante
Behauptung: Konstante = 2· a
Zur Begründung betrachten wir den Punkt P auf der x-Achse ( siehe Abb. 2) und stellen fest: L1 + L2 = (a - e) + (a + e) = 2· a
[(x-e)2 + y2 ] ½ = 2·a - [(x+e)2 + y2 ] ½ → (x-e)2 + y2 = 4·a2 + (x+e)2 + y2 - 4· a · [(x+e)2 + y2 ] ½
beide Seiten wurden quadriert !
↓
4·a2 + (x+e)2 + y2 - (x-e)2 – y2 = 4· a · [(x+e)2 + y2 ] ½
↓
e·x + a2 = a · [(x+e)2 + y2 ] ½ → e2 · x2 + a4 + 2·e·x·a2 = a2 · [(x+e)2 + y2 ]
↓
e2 · x2 + a4 + 2·e·x·a2 = a2 · x2 + a2 · e2 + 2·e·x·a2 + a2 · y2
e2 = a2 – b2
↓
a2 · x2 - b2 · x2+ a4 + 2·e·x·a2 = a2 · x2 + a4 - a2 · b2+ 2·e·x·a2 + a2 · y2
↓
- b2 · x2 = - a2 · b2 + a2 · y2 → x2 / a2 + y2 / b2 = 1 (Ellipsengleichung)
↓
|y| = b · (1 - x2 / a2 )½ → y = b · (1 - x2 / a2 ) ½ ; y = - b · (1 - x2 / a2 ) ½
Nach der Eingabe von „36“ und „START“ erscheint eine errechnete Planetenbahn zusammen mit den hier angegebenen Funktionsgleichungen. Es kann gezeigt werden, dass x2 / a2 + y2 / b2 = 1 die Planetenbahn beschreibt.
Anmerkung:
Es liegt nahe, die Ellipsengleichung mit dem Term z2 / c2 zu ergänzen. Alle Punkte, deren Koordinaten die Gleichung x2 / a2 + y2 / b2 + z2 / c2 = 1 erfüllen, bilden ein Ellipsoid (siehe Abb. 3).
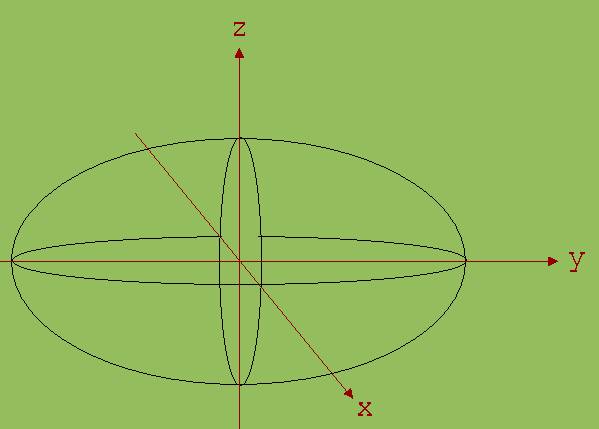
Abb. 3