Aufgaben

Die Lösungen zu diesen Aufgaben finden Sie in der zweiten Hälfte dieser Seite !

Zur Behandlung der hier gegeben Aufgaben muss das Additionsgesetz der Kräfte bekannt sein, welches erst in den folgenden Kapiteln behandelt wird. Dieses Gesetz besagt:

Wirken auf einen Körper K zwei Kräfte F1 und F2 , dann verhält sich der Schwerpunkt von K so, als ob nur eine der Vektorsumme von F1 und F2 gleichende Kraft F3 auf ihn einwirke.





1. Ein kleiner mit Wasser gefüllter Eimer wird in einer vertikalen Ebene auf einer Kreisbahn mit r = 0,8 m gedreht.

Welche Geschwindigkeit muss der Eimer am höchsten Punkt seiner Bahn mindestens haben, wenn das Wasser nicht auslaufen soll ?



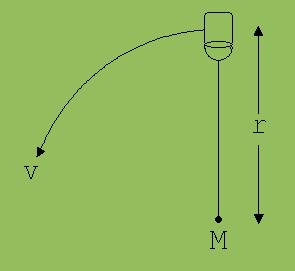
2. Ein Auto fährt in einer ebenen Kurve mit dem Radius r = 50 m.

Welche Geschwindigkeit v darf das Auto maximal haben, wenn es nicht aus der Kurve heraus rutschen soll ?

Der Reibungskoeffizient µ betrage 0.9.




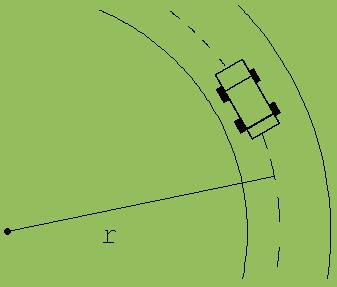
3. Wenn die Straße glatt ist (vernachlässigbarer Reibungskoeffizient ), dann muss sie in einer Kurve nach dem äußeren Kurvenrand hin ansteigen, wenn ein Auto nicht aus der Kurve heraus rutschen soll.

Wie groß muss der Anstiegswinkel α in einer Kurve mit dem Radius r = 50 für ein Auto mit 100 km/h sein ?



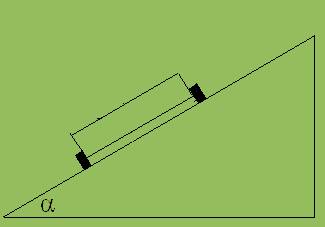
4. Mit v = 20 km/h fährt ein Radfahrer in eine Kurve, deren Radius r = 20 m beträgt.

Mit welchem Winkel α legt sich der Radfahrer hierbei in die Kurve ?



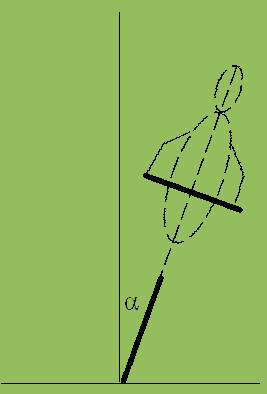
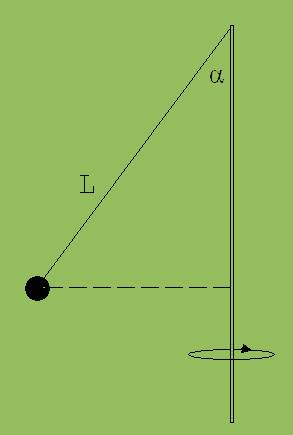
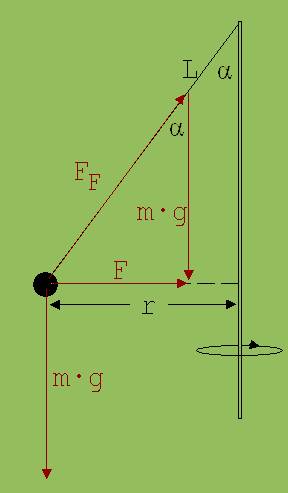
5. Am oberen Ende eines rotierenden senkrechten Stabes ist eine Kugel mit einem Faden der Länge L = 50 cm angebunden. Sie dreht sich mit der Winkelgeschwindigkeit ω = 10 ·1/s. Welchen Winkel α bildet der Faden mit dem Stab ?



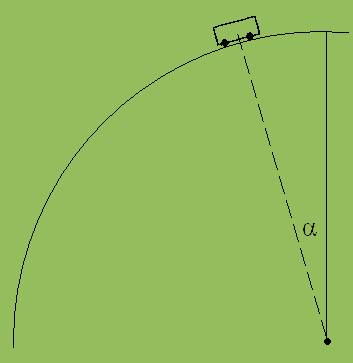
6. Auf die höchste Stelle eines Rohres mit dem Radius r = 0,5 m wird ein Experimentierwagen gesetzt. Nach einem leichten Stoß rollt es reibungsfrei abwärts. Bei welchem Winkel α löst es sich vom Rohr ?




7. Ein Hohlkugel mit dem Volumen V sei mit Gas gefüllt. Dieses Gas bestehe aus n Teilchen der Masse m, die immer wieder mit der Geschwindigkeit v auf die Innenwand der Hohlkugel stoßen und damit einen Druck p auf diese Wand bewirken. Wir setzen voraus, dass die Kraft der Teilchen auf die Gefäßwand nicht vom Verlauf der Teilchenbahn abhängt, dass es in bezug auf die Kraft gleichgültig ist ob ein Teilchen immer wieder auf die Wand stößt oder an ihr entlang gleitet.

  1. Wie hängt der Druck p von V, n, m und v ab ?

  2. Welche Geschwindigkeit hat ein Sauerstoffmolekül in einem Behälter mit V = 22 Liter der 32 g Sauerstoff unter 1 bar enthält.







Lösungen

Zu 1.:

Der Boden des Eimers und die Erde üben Kräfte auf das Wasser aus. Am höchsten Punkt ist die Summe aus der Bodenkraft FB und der Gewichtskraft m · g die Zentripetalkraft auf das Wasser der Masse m.

m ·g + FB = m ·v2 /r


Ist FB = 0, dann hält sich das Wasser gerade noch im Eimer.


m·g = m ·v2 /r    →    g = v2 /r    →    v2 = g·r    →    v = 2,8 m/s




Zu 2.:

Die Zentripetalkraft geht von der Straße aus. Sie beträgt höchstens µ ·m ·g.


µ ·m ·g = m ·v2 /r    →   µ ·g = v2 / r   →    v2 = µ ·g · r   →   v = 21 m/s = 75.6 km/h


Hinweis:

In der Aufgabenstellung wird man zunächst eine Angabe über die Masse m vermissen. Wenn eine Zahlenangabe zu fehlen scheint, dann sollte man eine Variable für sie setzten in der Hoffnung, dass diese bei der Behandlung der Aufgabe durch Kürzen herausfällt.



Zu 3.:

Die Straße und die Erde üben die Kräfte FB und m · g auf das Auto aus. Die Zentripetalkraft F ist die Resultierende aus diesen beiden Kräften.


tan α = F / (m · g );   F = m ·v2 /r   →   tan α = v2 /(g · r)   →    α = 57°





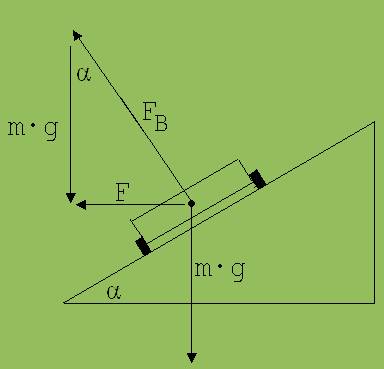
Zu 4.:

Die Straße und die Erde über auf den Fahrer und das Fahrrad die Kräfte FB und m·g aus ( m = Masse des Fahrrads + Masse des Fahrers).


tan α = F / (m · g);     F = m ·v2 /r   →    tan α = v2 / (r · g)   →   α = 8,9 °






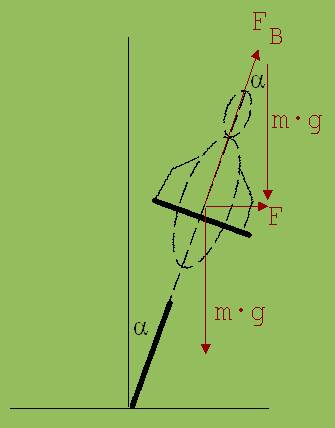
Zu 5.:

Der Faden und die Erde wirken mit den Kräften FF und m · g auf die Kugel ein. Die Resultierende dieser beiden Kräfte wirkt als Zentripetalkraft F.


tan α = F/(m · g);    F = m · ω2 · r   →    tan α = ω2 · r/ g

r = L · sin α;    sin α / cos α = ω2 · r/ g    →    sin α / cos α = ω2 · L · sin α /g    →    1/cos α = ω2 · L /g

→    cos α = g /(ω2 · L )    →    α = 78°






Zu 6.:

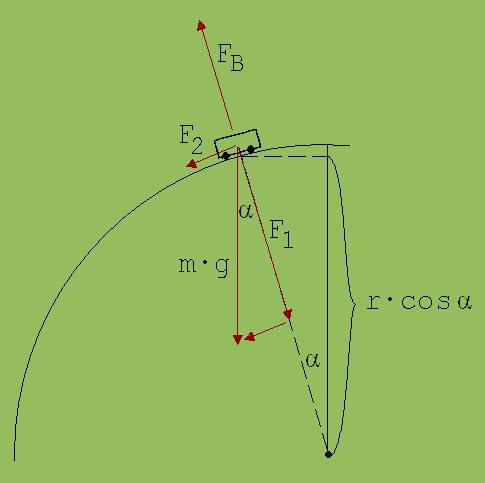
Die Gewichtskraft kann man in die zwei Komponenten F1 und F2 zerlegen. F2 sorgt für die Beschleunigung entlang der Bahn. F1 bildet mit FB die Zentripetalkraft. FB ist die Kraft, welche das Rohr auf das Wägelchen ausübt. An der Ablösestelle ist FB = 0.

In diesem Fall gilt: F1 = m · v2 /r ; F1 = m · g · cos α    →    m · g · cos α = m · v2 /r    →    cos α = v2 /(r · g)

v2 ist durch die Höhenänderung h = r - r · cos α = r · ( 1 – cos α ) bestimmt.

Es gilt : v2 = 2 ·g · h = 2 ·g · r · ( 1 – cos α )

v2 = 2 ·g · h = 2 ·g · r · ( 1 – cos α ) ; cos α = v2 /(r · g)

↓

cos α = 2 ·g · r · ( 1 – cos α ) / (r · g ) = 2 · ( 1 – cos α )    →    cos α = 2/3    →    α = 48°





Zu 7. :

1. Wir denken uns ein Teilchen der Masse m, dass mit der Geschwindigkeit v an der Innenseite der Kugelwand entlang gleitet. Die Hohlkugel mit dem Innenradius r übt die Zentripetalkraft m · v2 / r auf das Teilchen aus. Die Wand erfährt eine gleich große Gegenkraft. n Teilchen verursachen die Kraft Fg = n · m ·v2 / r. Den Druck p auf die Wand erhalten wir nach p = Fg / (4 · π · r2 ).

p = n · m· v2 /(4 · π · r2 )

Unter Berücksichtigung von V = (4/3) · π · r3 gelangt man zu: p = 1/3 · n · m· v2 /V → p · V = 1/3 · n · m· v2


2.

n · m = 32 g = 0,032 kg; V = 22 Liter = 0,022 m3; 1 bar = 105 N/m2

v2 = 105 N/m2 · 0,022 m3 · 3 / 0,032 kg = 206250 m2 / s2 → v ≈ 454 m/s