Die Lösungen zu diesen Aufgaben finden Sie in der zweiten Hälfte dieser Seite !
1. Ein Gegenstand wird mit v0 = 10 m/s senkrecht nach oben geworfen.
Welche Höhe erreicht er und wie lange dauert der Wurf ?
2. Ein Gegenstand wird mit v0 = -5 m/ s von einem y0 = 10 m hohen Turm senkrecht nach unten geworfen.
Wie lang ist die Wurfzeit ?
Mit welcher Geschwindigkeit schlägt der Gegenstand auf den Boden ?
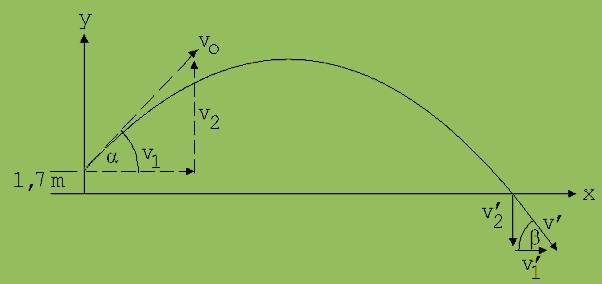
3. Ein Ball wird mit 15 m/s unter dem Höhenwinkel 45° aus 1,7 m Höhe nach oben geworfen.
Welche Höhe erreicht der Ball ?
Wie weit fliegt der Ball ?
Mit welcher Geschwindigkeit und unter welchem Winkel schlägt der Ball auf den Boden ?
Lösungen
Zu 1.:
Der Gegenstand erreicht in der Zeit t seinen höchsten Punkt mit der Koordinaten y ( am Koordinatenursprung beginnt der Wurf) und hat dann die Geschwindigkeit 0.
Die Geschwindigkeitsänderung in t ist somit v0 .
v0 / t = g ; t = v0 / g = 10m/s / 9,81m/s2 = 1,02 s
y = - ½ · g ·t2 + v0 ·t = 5,1 m
Wurfdauer tW = 2·t = 2,04 s
Zu 2.:
Am Ort des Aufschlags sei der Ursprung eines Koordinatensystems, dessen y-Achse nach oben weist.
y = - ½ ·g · t2 + v0 · t + y0 ; beim Aufschlag gilt : y = 0 → - ½ · g · t2 + v0 · t + y0 = 0
Es handelt sich um eine quadratische Gleichung mit den Lösungen: t1 = - 2s (unpassend) und t2 = 1s
v = -g·t + v0 ; v = - 9,81 m/s2 · 1 s – 5 m/s ; v = - 14,81 m/s
Zu 3.:

v1 = v0 · cos α ; v2 = v0 · sin α
Wurfhöhe
Am höchsten Punkt ist v2 = 0; t ist die Steigzeit
v2 / t = g → t = v2 / g
y = - ½ ·g · t2 + v2 · t + y0 ( y0 = 1,7 m )
→ y = - ½ ·g · v22 / g2 + v22 / g + y0
→ y = ½ · v22 / g +y0
→ y = ½ · v02 · sin2(α) / g + y0
y = 7,4 m
Wurfweite
y = - ½ · g · t2 + v2 · t + y0 ( t steht nun für die Wurfzeit ). Beim Aufschlag gilt : y = 0
→ 0 = - ½ · g · t2 + t· v0 · sin α + y0 (quadratische Gleichung für t ); t1 = - 0,15 s (unpassend) ; t2 = 2,3 s
Wurfweite x = v1 · t2 = v0 · (cos α ) · t2; x = 24,4 m
Geschwindigkeit des Aufschlags:
Vektor v der Endgeschwindigkeit: v = v0 + a· t = {v0 · cos(α) ; v0 · sin(α) - g· t2 } = { 10,6 m/s= v’1; -12 m/s = v’2}
|v| = 16 m/s
tan β = 12 / 10,6 ; β = 48, 5°
tan (α ) bedeutet im Rechenfenster von „Mathe.-Physik“ den Tangens zum Bogenmaß α
tang(α) bedeutet den Tangens zum Gradmaß α (Altgrad)
arctan(x) gibt das Bogenmaß und arctang(x) das Gradmaß an.
Entsprechendes gilt für sin und cos.
Quadratische Gleichungen können sofort mit „Mathe._ Gleichungen n. Grades“ gelöst werden ( „48“ und „START“).
Eine quadratische Gleichung kann auch im Rechenfenster gelöst werden. Zur Lösungen von 0 = - (g/2) · t2 + t· v0 · sin α + y0 wird gl(t): 0 = - (g/2) * t^2 + t *v *sing(a) + y in das Rechenfenster geschrieben. Nach einem Doppelklick auf der Zeile dieser Gleichung werden die beiden Lösungen angegeben. Selbstverständlich müssen g, v, a und y zunächst festgelegt werden.