Fourier-Analyse von Klängen mit Hilfe der Programme Audacity (Freeware) und Mathe.-Physik

Bei der Behandlung der Kreisfunktionen werden Sin- und Cos-Funktionen addiert. Interessant wird diese Thematik für Schüler erst dann, wenn sie erfahren, dass jede periodische Funktion durch eine Summe von Sin-Funktionen beschrieben, bzw. in eine Summe von Sin-Funktionen zerlegt werden kann. Dies ist vor allem im Hinblick auf Klänge interessant, denn damit ist eine Analyse nach Grund-und Obertönen möglich.

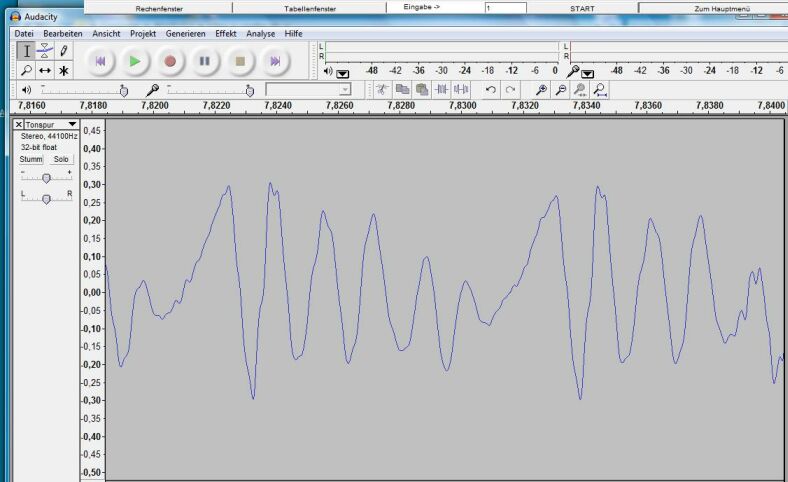
Hier wird nun die Durchführung einer solchen Analyse mit dem Programm „Mathe.-Physik“ beschrieben. Analysiert wird das Klangdiagramme des Vokals a, welches mit dem Programm „Audacity“ ( Freeware, kann aus dem Internet geholt werden) aufgenommen wurde. Es wird mit der Taste „Drucken“ kopiert und in das Bildfenster von „Mathe.-Physik“ eingefügt (siehe Abb.1).

Abb. 1

Damit den Diagrammabschnitten richtige Zeiten zugeordnet werden, erfolgt eine Kalibrierung des Bildfeldes in horizontaler Richtung. Zu diesem Zweck wird „Mathe._Kalibrieren_Kalibrieren in x-Richtung“ gewählt (siehe Abb. 2). Hiernach erscheint ein Kreuz auf dem Bildfeld, mit ihm werden nebeneinander liegende Punkte angeklickt (Linksklick), deren zugehörende Zeiten bekannt sind. Die Zeitdifferenz wird hiernach mit der Maßeinheit eingegeben. Zur Kalibrierung sind die Zeitangaben 7,8200 s, 7,8220 s... über dem Diagramm zu nutzen.

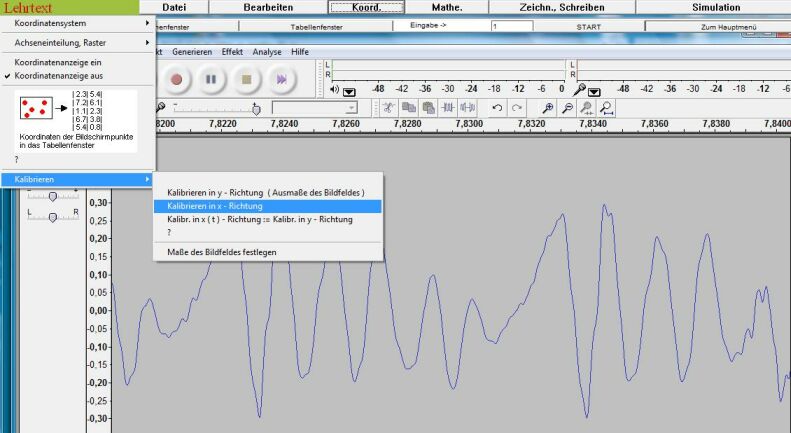
Abb. 2

Nach Anklicken von „Mathe_Fourieranalyse“ (siehe Abb. 3) wird eine Periode aus dem Diagramm mit einem Rechteck eingegrenzt (siehe Abb.4).

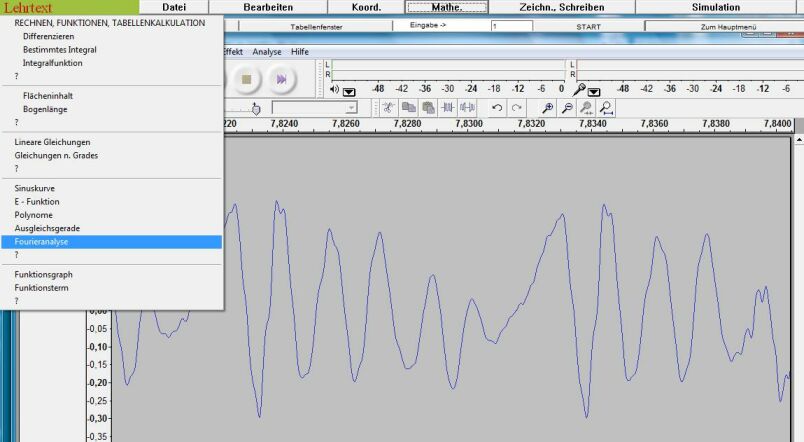
Abb. 3

Mit einem Linksklick wird ein Eckpunkt des Rechtecks gesetzt, mit gedrückter Maustaste wird es aufgespannt und mit der Entlastung dieser Taste fertiggestellt (siehe Abb. 4). Es ist darauf zu achten, dass im markierten Bereich über dem Diagramm keine Punkte mit einer anderen Farbe als Grau oder Weiß liegen. Der Rechner sucht vom oberen Rand des Rechtecks ausgehend die nicht grauen oder weißen Punkte des Diagramms, ermittelt deren Koordinaten und bestimmt a₁ · sin(ω · t + φ₁) , a₂·sin(2 · ω · t + φ₂ ) …

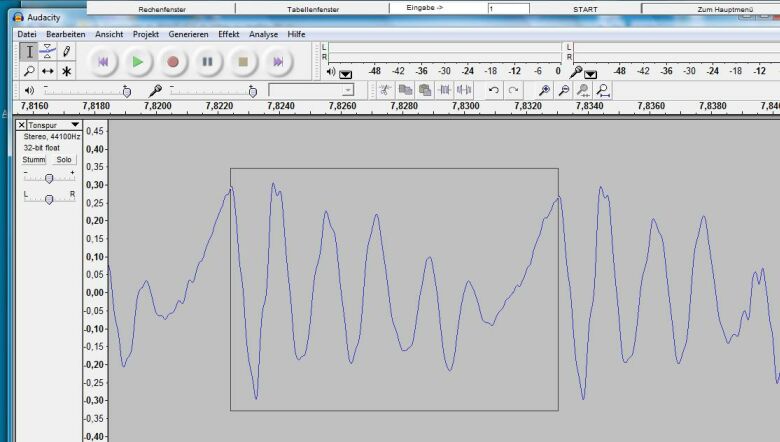
Abb. 4

Hiernach erscheint eine Abfrage mit „Nach und nach“ und „Alle zugleich“(siehe Abb. 5).

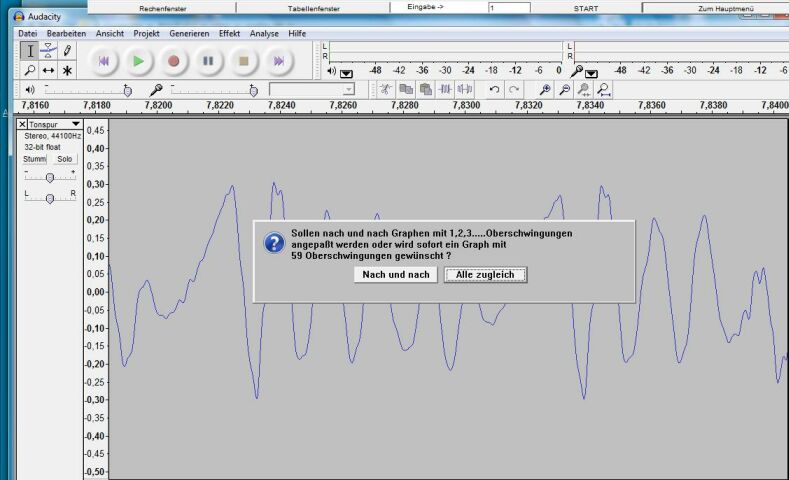
Abb. 5

Bei der Wahl von „Nach und nach“ zeichnet der Rechner den Graphen zu y = a₁ · sin( ω · t + φ₁) und eine waagrechte Mittellinie (siehe Abb. 6).

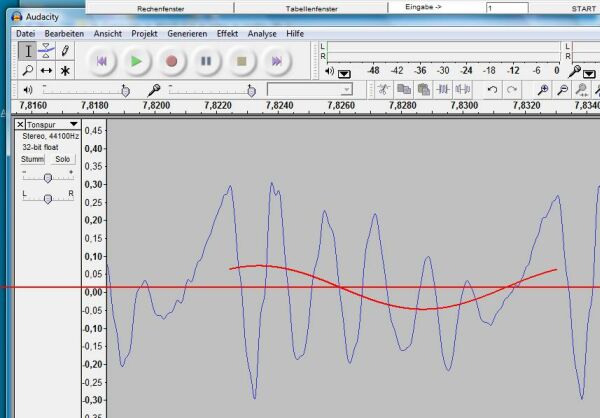
Abb. 6

a₁· sin( ω · t + φ₁): Grundschwingung

a₂· sin(2 · ω · t + φ₂): 1. Oberschwingung

a₃· sin(3 · ω · t + φ₃): 2. Oberschwingung

Nach Anklicken von „ Es werden mehr als 0 Oberschwingungen gewählt “ (siehe Abb. 7) erscheint zunächst der Graphen zu y = a₁· sin(ω · t + φ₁) + a₂· sin(2 · ω · t + φ₂), dann mit dem nächsten Anklicken der zu y = a₁· sin( ω · t + φ₁) + a₂· sin(2 · ω · t + φ₂) + a₃· sin(3 · ω · t + φ₃) usw. . Das Verfahren wird dann abgebrochen, wenn der Graph von y = a₁· sin( ω · t + φ₁) + a₂· sin(2 · ω · t + φ₂) + a₃· sin(3 · ω · t + φ₃).... nur noch wenig von der ursprünglichen Kurve abweicht (siehe Abb. 8).

Abb. 7

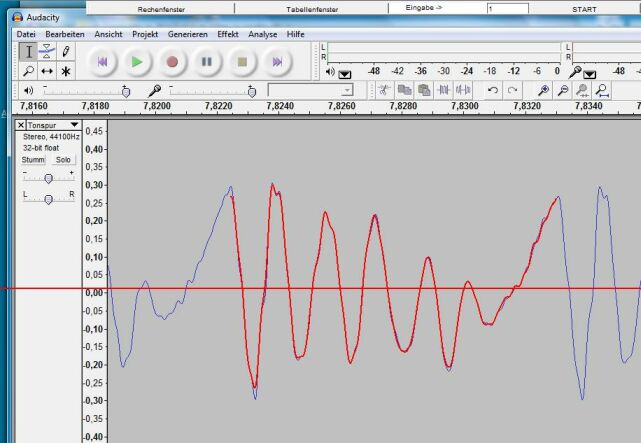
Abb. 8

Hiernach werden die einzelnen Amplituden a₁, a₂, a₃, a₄ .... in einem Säulendiagramm angezeigt (siehe Abb.9).

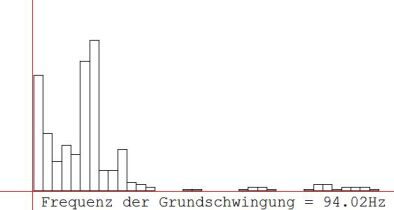
Abb. 9

Nach Wahl von „Funktionsterm _Summe der Schwingungsterme" unter „Mathe.“ (siehe Abb. 10) ist die zum Graphen gehörende Funktionsgleichung im Rechenfenster zu sehen (siehe Abb. 11).

Abb. 10

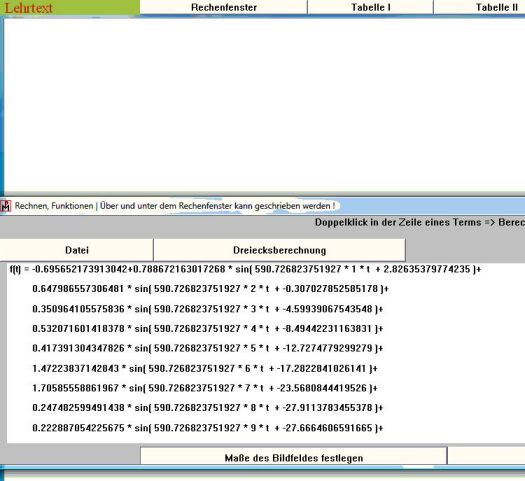
Abb. 11

Eine grafische Darstellung ist möglich (siehe Abb. 12). Nach einem Doppelklick auf der Funktionszeile erscheint eine bewegliche, senkrechte Strecke zur Angabe des Darstellungsintervalls. Die Intervallgrenzen werden mit einem Linksklick markiert. Der Graph entsteht. Nach einem Rechtsklick wird der Graph über das gesamte Bildfeld gezeichnet. Ist der Graph gezeichnet, dann können Ausschnitte gebildet werden.

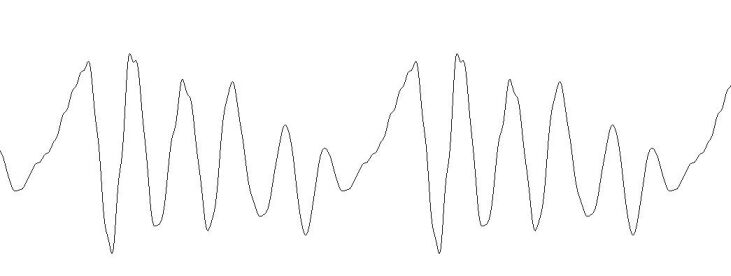
Abb. 12