3.3.3 Arbeit und Leistung des elektrischen Feldes
3.3.3.1 Arbeit des Feldes
Wenn Elektronen vom – Pol zum +Pol eines elektrochemischen Elements fließen, dann werden sie vom elektrischen Feld geschoben und erhalten dementsprechend Energie aus diesem Feld. Da die beweglichen Ladungen hierbei über den Leiter gleichmäßig verteilt bleiben ( geladene Leiterabschnitte sind nicht erkennbar), kann auf eine konstante Elektronengeschwindigkeit geschlossen werden.
Was geschieht mit der Energie der Elektronen ?
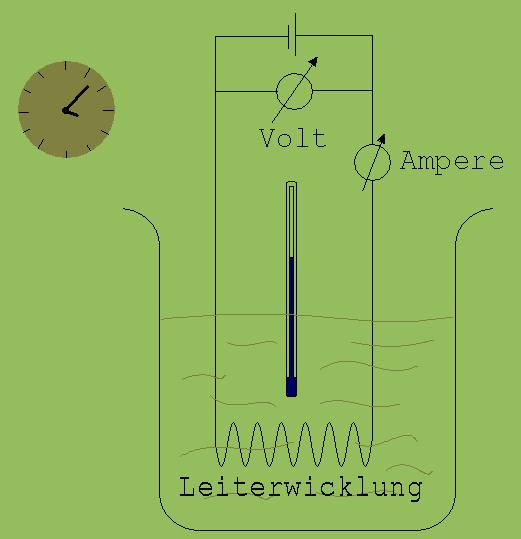
Die Elektronen stoßen auf Atome des Leiters und geben so ihre gewonnene kinetische Energie immer wieder an die Atome des Leiters ab. Die Zunahme an Bewegungsenergie bei den Atomen des Leitermaterials macht sich am Leiter als Temperaturanstieg bemerkbar. Taucht der Leiter in Wasser, dann geben seine Atome ihre beim Zusammenstoß mit Elektronen gewonnene Energie fast vollständig an die Atome des umgebenden Wassers ab. Mit der in Abb. 1 dargestellten Anordnung kann diese Energie gemessen werden.

Abb. 1
Die Atome in der Leiterwicklung geben ihre Energie E an das Wasser ab und bewirken somit in einer Zeit Δt eine Temperaturänderung ΔT.
E = m ·cW ·ΔT; m: Masse des Wassers ; cW: Spezifische Wärmkapazität des Wassers
Die spezifische Wärmekapazität eines Materials beschreibt die Energie, die notwendig ist, um eine Masseneinheit (z.B. 1g) dieses Materials um 1 K zu erwärmen. m ·cW steht für die Energiezunahme der Gesamtmasse m bei einer Temperatursteigerung um 1 Kelvin und m·cW·ΔT für den Energiezuwachs nach Erwärmung um ΔT.
Spezifische Wärmekapazität = E/(m · Δt)
Die an das Wasser abgegebene Energie ist gleich der vom elektrischen Feld beim Verschieben der Ladung Q verrichteten Arbeit W.
W/Q = U → W = U · Q
Um welchen Wert ΔT steigt die Temperatur in einer Zeit Δt an ?
Unter Berücksichtigung von I = Q/Δt ( I: Stromstärke) ↔ Q = I ·Δt kann geschrieben werden:
W = I · Δt · U
W = E
E = m ·cW ·ΔT
↓
I · Δt · U = m ·cW ·ΔT
↓
ΔT = I · Δt · U/ (m ·cW)
Da diese Gleichung einer experimentellen Nachprüfung standhält, können die Voraussetzungen für die Spannungsmessung z.B. E = σ/ ε0 als richtig angesehen werden.
3.3.3.2 Leistung des Feldes
Die Arbeit des Feldes wird nach W = U · Q = I · Δt · U berechnet. Für seine Leistung P = W/ Δt (Arbeit in der Zeiteinheit) gilt somit:
P = I· U
Die Einheit Volt · Ampere = Joule/Sekunde heißt Watt (W) .