1.11 Trägheitskräfte
1.11.1 Was versteht man unter einer Trägheitskraft
Ein Omnibus fährt mit der Beschleunigung a an. Hierbei fällt ein im Omnibus frei stehender Passagier nach hinten. Er führt seine Beschleunigung im Omnibus auf eine der Erdanziehungskraft vergleichbare Kraft zurück, die ihn nach hinten zieht. Hält er sich an einem Sitz fest, dann wird er mit F = m · a beschleunigt. Er meint jedoch, eine Kraft FT = - m·a drücke ihn nach hinten und werde von einer vom Sitz ausgehenden Gegenkraft ausgeglichen. FT ist eine Scheinkraft in einem beschleunigten System S; wir nennen sie Trägheitskraft.
Für eine Kraft F (z.B. für die vom Sitz des Omnibusses ausgehende Kraft) auf einen Körper K mit der Masse m in einem beschleunigten System S gilt:
F = m·a ; a = aB + a' ; F = m· aB + m·a'; m·a' = F – m·aB .
aB ist der durch die Systembeschleunigung verursachter Anteil der Beschleunigung und a' ist die Beschleunigung von K innerhalb von S. Für einen Beobachter in S ist m·a' gleich der Summe der auf K wirkenden Kräfte. Nach seiner Sichtweise wirkt neben F noch die Trägheitskraft – m·aB. Wenn er meint, in einem ruhenden System zu sein, dann muss er bei seinen Rechnungen diese Trägheitskraft – m·aB berücksichtigen, nur dann kann er die Vorgänge in S richtig berechnen. Hält er sich im Omnibus an einem Sitz fest, dann gilt: F – m·aB = 0. In diesem Fall ist die Trägheitskraft dem Betrage nach gleich der Kraft des Sitzes. Die bekanntesten Trägheitskräfte sind die Zentrifugal- und die Corioliskraft, es sind Trägheitskräfte in einem rotierenden Raum.


Abb. 1.11.1 Abb. 1.11.2
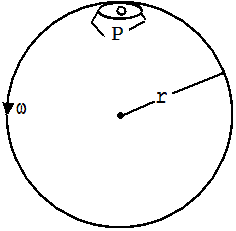
Abb. 1.11.1 zeigt einen rotierenden, zylindrischen Raum in der Draufsicht ( Rotor auf einem Jahrmarkt ). Ein an der Außenwand stehender Mann P wird von einer Zentripetalkraft F = m·ω2· r auf einer Kreisbahn gehalten. P übt eine gleich große Gegenkraft FT auf die Wand aus. Da sich P im rotierenden Raum als ruhend ansieht, erkennt er FT nicht als Reak-tion auf die beschleunigende Kraft der Wand. Er deutet sie stattdessen als eine ausder Ferne wirkende Kraft, der Gravitationskraft vergleichbar, die von ihm an die Wand weitergegeben wird und nennt sie Zentrifugalkraft.
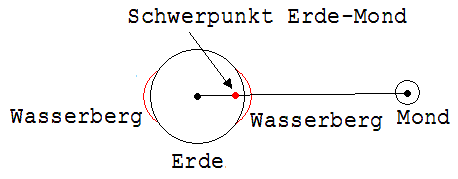
Hier ist es angebracht auf das Zustandekommen von Ebbe und Flut einzugehen. Erde und Mond drehen sich um einen gemeinsamen Schwerpunkt (siehe Abb. 1. 11.2). Das Wasser der Meere unterliegt deshalb nicht nur der Anziehungskraft FM des Mondes, sondern auch noch der durch die genannte Drehung bedingten Zentrifugalkraft FZ . In der Erdmitte heben sich die beiden Kräfte auf. Auf der dem Mond abgewandten Seite überwiegt die Zentrifugalkraft und führt zur Bildung eines Wasserberges. Auf der dem Mond zugewandten ist die Anziehungskraft des Mondes größer als die Zentrifugalkraft, rechts vom Schwerpunkt hat sie sogar die gleiche Richtung wie die Zentrifugalkraft. Auch dort entsteht infolgedessen ein Wasserberg. Die Erde dreht sich unter diesen Wasserbergen. Aus der Sicht eines Erdenbewohners laufen in 24 Stunden zwei Wasserberge über die Erdkugel, die sich jeweils mit einer Flut ankündigen.
Aufgaben
1. Ein Kind dreht sich in einem Kettenkarussell so, wie dies in der Abb. 1.11.3 angedeutet ist.Welche Geschwindigkeit hat das Kind ?
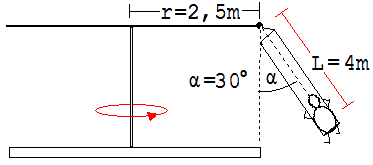
Abb. 1.11.3
2. Eine mit Wasser gefüllte Küvette rotiert mit der Winkelgeschwindigkeit ω = 15 s-1 um ihre Symmetrieachse. Hierbei bildet das Wasser eine parabelförmige Oberfläche aus. Bestimme den Funktionsgrafen y = k·x2 der zugehörenden Parabel !
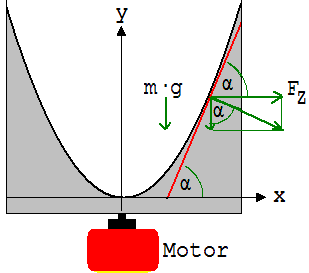
Abb. 1.11.4
3. Auf einer um eine senkrechte Achse mit der Winkelgeschwindigkeit ω = 2 s-1 rotierenden Scheibe schwingt eine von einem Stab geführte Kugel K der Masse m = 100 g um den Scheibenmittelpunkt. Die Schwingungsfrequenz der Kugel auf einer ruhenden Scheibe beträgt 1 Hz. Mit welcher Frequenz schwingt die Kugel auf der rotierenden Scheibe ?
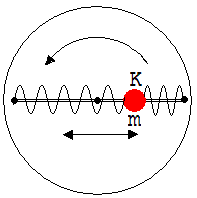
Abb. 1.11.5
1.11.3.1 Der Coriolis-Durchflussmesser
In Abfüllanlagen findet man manchmal große, vibrierende Röhren, mit denen durchfließende Flüssigkeitsmassen mit sehr hoher Genauigkeit gemessen werden können. Es heißt, die Fließgeschwindigkeit (der Massedurchfluss) werde mit Hilfe einer Corioliskraft bestimmt.
Was ist dies für eine Kraft und wie kommt sie zustande?

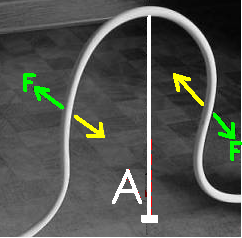
Abb. 1. 11.6 Abb. 1.11.7
In Abb. 1.11.6 sehen wir ein gebogenes, von Wasser durchflossenes Rohr (Fließgeschwindigkeit v). Wenn dieses am Boden befestigte Rohr so zum Schwingen angeregt wird, wie es die beiden Pfeile am Scheitel des Rohrs in der Abb. 1.11.6 anzeigen, dann machen sich am linken und rechten Schenkel hin- und her biegende Kräfte F bemerkbar, unter denen das Rohr noch eine Drehschwingung um die in der Abb. 1.11.7 gezeichnete Achse A ausführt. Die zur Strömungsgeschwindigkeit v proportionale Amplitude dieser Drehschwingung ermöglicht die Bestimmung von v mit sehr hoher Genauigkeit. Im Handel (Hersteller: Firma Endress+Hauser in Reinach bei Basel) gibt es Coriolis-Masseflussmeßgeräte für unterschiedlichen Bedarf über mehr als sieben Größenordnungen (von etwa 20 mg/s bis etwa 600 kg/s) mit großer Genauigkeit (0,1%).
Wie kommt es zu diesen Kräften F ?
Zur Erklärung dient die Abb. 1.11.8 auf der nächsten Seite. Zu sehen ist eine kleine Lokomotive L auf einer Schiene, die auf einer mit der Winkelgeschwindigkeit ω rotierenden Scheibe liegt. Die in Bezug auf die Scheibe mit konstanter Geschwindigkeit v fahrende Lokomotive habe zum Zeitpunkt t = 0 die Rotationsachse überquert. Zu diesem Zeitpunkt sei die x-Achse eines über der Scheibe ruhenden Koordinatensystem in Fahrtrichtung ausgerichtet worden.
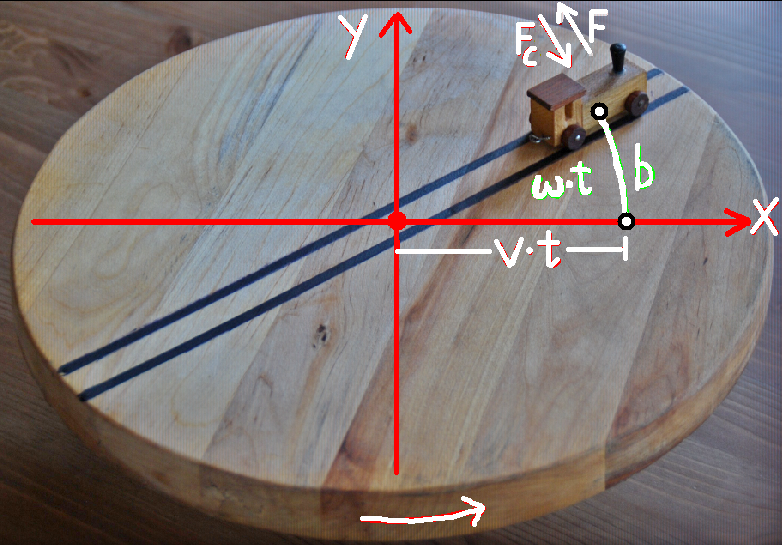
Abb. 1.11.8
Die Lokomotive L übt wie das Wasser im U-Rohr eine Kraft FC quer zur Bewegungsrichtung aus. Die Existenz dieser auf die Schiene wirkenden Kraft FC kann hier leicht begründet werden. L bewegt sich aus der Sicht eines auf die Scheibe schauenden, ruhenden Beobachters B nicht nur entlang der Schiene. Infolge der Rotation wird L in Richtung der y-Achse beschleunigt. Dieser Beschleunigung ist die Kraftkoordinate Fy = m · ay zuzuordnen. Wenn die x-Achse des Koordinatensystems mit der Schiene einen sehr kleinen Winkel bildet, dann steht Fy für eine zur Fahrtrichtung orthogonale Kraftkomponente Fq , mit der die Schiene auf die Lokomotive einwirkt. Ein auf der rotierenden Scheibe sitzender Beobachter B' kann keine Beschleunigung an der Lokomotive erkennen. Für ihn bewegt sie sich gleichförmig auf einer geraden Spur und erfährt keine beschleunigende Kraft durch die Schiene.
Ihm fällt aber die nach dem Wechselwirkungsgesetzt zu erwartende Gegenkraft FC zu Fq auf, welche die Lokomotive auf die Schiene ausübt und er denkt sich, die Lokomotive übertrage eine aus der Ferne wirkende Kraft auf die Schiene. Er nennt sie Corioliskraft (nach dem französischen Mathematiker Coriol).
Der y-Wert, den L nach Überqueren der Rotationsachse in einer Zeit t annimmt, weicht bei kleinem t (kleiner Winkel) nur wenig vom Bogen b ab, weshalb unter dieser Bedingung y = b geschrieben werden kann.
ω·t = b / (v·t) Bogenmaß ! → y = b = ω· v · t2
v ist die Geschwindigkeit der Lokomotive aus der Sicht von B'.
Bekanntlich beschreibt ein solcher Term mit t2 eine Bewegung mit konstanter Beschleunigung ay.
Es gilt : y = (ay /2) · t2 ; y = ω· v · t2 → ay = 2 · v · ω → Fy = 2 · m · v · ω
Bei jeder Bewegung auf der rotierenden Scheibe wirkt aus der Sicht von B' eine Corioliskraft FC = 2 · m · v · ω ( Gegenkraft zu Fq) quer zur Bewegungsrichtung auf den bewegten Körper. Ein das bewegte Objekt begleitender Beobachter registriert bei einer Linksdrehung (Draufsicht) eine nach rechts und bei einer Rechtsdrehung eine nach links wirkende Corioliskraft.
Messung der vom Wasserstrom verursachten Corioliskraft

Abb. 1.11.9
Zum Nachweis dieser Kraft im Unterricht eignet sich die in Abb.1.11.9 dargestellte Anordnung. Zu sehen ist ein von Wasser durchflossenes U-Rohr mit der Höhe r und der Breite b, welche um eine waagrechte Achse pendelt, die von der beweglichen Glasplatte der Wippe gehalten wird. Ein Elektromotor bewirkt ein gleichmäßiges Pendeln. Er dreht ein Rad mit einem exzentrisch, parallel zu Drehachse angebrachten Stäbchen S. Das mit der Geschwindigkeit vS rotierende Stäbchen S ist über einen Faden mit dem U-Rohr verbunden. Ein an der Hinterwand angebundener Gummifaden (gestrichelt) sorgt dafür, dass dieser Faden während der Drehung von S gespannt bleibt. Die Schenkel des U-Rohrs rotieren mit veränderlicher Winkelgeschwindigkeit ω, sie haben in senkrechter Stellung die höchste Winkelgeschwindigkeit
ω = vS/r.
Wir stellen uns einen parallel zu Pendelachse ausgerichteten Beobachter B vor (siehe Abb. 1.11.9), der auf dem linken Schenkel des Rohrs der Strömung folgt. Da das Rohr zu seinen Füßen ein rotierendes System ist, wirken aus seiner Sicht auf das im linken und rechten Schenkel fließende Wasser einander entgegen gerichtete, seitliche Corioliskräfte mit den Beträgen FC = 2· m ·vW · ω.
m: Masse des Wassers in einem senkrechten Schenkel des U-Rohrs; vW: Strömungsgeschwindigkeit des Wassers
Sind die Schenkel des U-Rohres genau nach unten gerichtet, dann wirken diese beiden Kräfte zusammen mit dem Drehmoment
M = 2 ·FC ·(b/2) = 2 · m · vW · ( vS/r) · b auf die Wippe.
b : Breite des U-Rohrs; b/2 : Hebelarm zu der Corioliskraft auf einen Schenkel
In einer Zeit t fließe das in einem senkrechten Schenkel vorhandene Wasser mit der Masse m aus dem U-Rohr.
vW = r/t ; M = 2 · m · (r/t ) · ( vS/r) · b = 2 · (m/t) · vS· b
m/t beschreibt den Massedurchfluss, die Masse die in einer Zeiteinheit aus dem Rohr fließt.
m/t = M/ ( 2 · vS · b)
Während des oben beschriebenen Experiments wurde das in der Abb. 1.11.10 sichtbare M-t-Diagramme aufgenommen. Die Amplitude des Diagramms zeigt das für die Berechnung von m/t nach m/t = M/ ( 2 · vS · b) notwendige Drehmoment M an. Mit diesem M = 0,09 N·m wurde für m/t der Wert 0,18 kg/s errechnet.
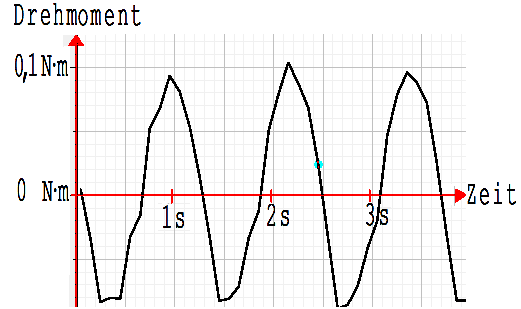
Abb. 1.11.10
Das Messergebnis kann man überprüfen, indem man das austretende Wasser kurzzeitig mit einem Eimer auffängt. Auch anhand der Reichweite des aus dem Rohr austretenden Wasserstrahls ist m/t bestimmbar. Somit ist die Prüfung der gewonnenen Ergebnisse leicht möglich. Bei dem hier beschriebenen Experiment wurde anhand der erwähnten Reichweite 0,17 kg/s ermittelt.
Anmerkung zur Messung:
Bemerkenswert ist, dass der Schlauch über die Mitte der Wippe in das U-Rohr eingeführt ist. Dieser Anschluss über der Wippenachse wurde gewählt, damit geringe Verschiebungen des Schlauchs nicht zu störenden Drehmomenten führen.
Das hier vorgestellte Experiment kann auch mit einem geschlossenen Wasserkreislauf vorgestellt werden. Passende Wasseranschlüsse sind somit nicht unbedingt erforderlich.
1.11.3.2 Pendel mit rotierender Masse (Pendelkreisel)
Ein interessantes Experiment zur Corioliskraft ist in der Abb. 1. 11.11 dargestellt. Am unteren Ende eines schwingenden Pendels (variable Winkelgeschwindigkeit des Pendels = ω’) rotiert ein 420 g schwerer Zylinder mit der Winkelgeschwindigkeit ω um die Achse eines Elektromotors. Wenn man den Halter des Pendels nicht fest in die Hand nimmt, dann weicht das Pendel quer zur Schwingungsebene aus (weißer Pfeil) und dreht hierbei den Haltegriff.

Abb. 1.11.11
Achtung !
Es kann nicht ausgeschlossen werden, dass sich der rotierende Eisenzylinder von der Welle des Motors löst. Deshalb sollte man beim Experimentieren mit dem Pendelkreisel immer einen Karton unter dieses Gerät stellen.
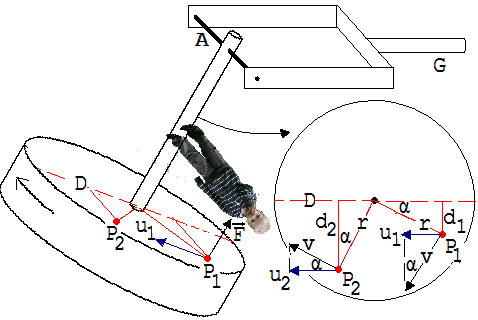
Abb. 1.11.12 Seitenansicht und Draufsicht
Wir betrachten das Geschehen aus der Sicht eines Beobachters B , der auf der Pendelstange parallel zur Pendelachse A steht (siehe Abb. 1.11.12). Für ihn sind Corioliskräfte F für das merkwürdige Verhalten des Pendels verantwortlich. Wir können uns den Zylinder in viele kleine Teile P1, P2 .. der Masse m’ zerlegt denken. Die zu einem solchen Punkt gehörende Geschwindigkeitskomponente u parallel zur Schwingungsebene verursacht eine Corioliskraft F auf P. Für die Corioliskraft auf den Punkt P1 gilt: F = 2·m’·ω’·u1 .
ω’ ist die augenblickliche Winkelgeschwindigkeit des Pendels. F ist nach oben gerichtet und demnach bestrebt, das Pendel mit dem Drehmoment 2 · m’ ·ω’ · u1 ·d1 nach vorne aus der Schwingungsebene zu drehen. d1 ist der Abstand des Punktes P1 von der Schwingungsebene der Pendelstange. Auf der dem Betrachter abgewandten Seite des Zylinders sind die Corioliskräfte nach unten gerichtet und haben somit den gleichen Drehsinn. Zur Berechnung des Drehmoments wählen wir zunächst zwei Massepunkte P1 und P2, deren Radien übereinstimmen und einen rechten Winkel miteinander bilden. Das Drehmoment dieses Punktepaars in Bezug auf den Durchmesser D rechnen wir aus. Hiernach kann leicht auf das Gesamtmoment Mg aller Massepunkte P geschlossen werden.
Für die Corioliskraft F auf P1 gilt : F = 2· m’ · ω’· u1 , u1 = v· sin α , v = ω· r
v: Umlaufgeschwindigkeit von P1 in Bezug auf die Zylinderachse
↓
F = 2 · m’ · ω’·ω· r · sin α
In Bezug auf den Durchmesser D des Pendels wirkt F mit einem Drehmoment M1.
M1= F·d1 = 2·m’ · ω’· ω · r · sin α · d1; d1 = r· sinα → M1 = 2 · m’·ω’·ω· r2 ·sin2 α
Für P2 finden wir: M2 = 2 · m’ · ω’· ω· r2 · cos2 α
M1 + M2 = 2 · m’ · ω’·ω· r2 · ( sin2 α + cos2 α ) = 2 · m’ · ω’·ω· r2
sin2 α + cos2 α = 1; 2 · m’ = m ist die Gesamtmasse beider Punkte.
↓
M1 + M2 = m · ω’·ω· r2
Addiert man die Drehmomente aller denkbaren Paare P1 , P2 , dann erhält man als Gesamtdrehmoment:
Mg = ω’ · ω · Σ m · r2
Σ m · r2 ist als Trägheitsmoment J des Zylinders bekannt.
Mg = ω’ · ω · J

Abb. 1.11.13
Zur Messung von Mg lässt man das Pendel genau über der Achse der Wippe schwingen. Während der Schwingung wird ein Diagramm gezeichnet, welches dem einer Schwingung ähnelt. Es zeigt an, dass unter dem Einfluss von Mg die Wippe um ihre Achse hin und her gedreht wird. Beim Schwingen durch die Ruhelage wird das Drehmoment in Bezug auf den Durchmesser D insgesamt auf die Wippe übertragen. Seine Größe kann am Diagramm abgelesen werden. Zur Kalibrierung der Wippe für Drehmomentmessung werden Gewichte auf den linken oder rechten Wippenrand gelegt.
1.11.4 Berechnung einer Bewegung in einem rotierenden System unter Berücksichtigung der Zentrifugal- und Corioliskraft
Die Bewegung in einem rotierenden System wird nur dann richtig berechnet, wenn man neben den wirklichen Kräfte auch noch die Zentrifugal- und die Corioliskraft in die Rechnung eingehen lässt.
Beispiel:
Wir stellen uns einen Massepunkt P vor, der sich auf einem ruhenden Strahl nach s = v·t (v = 4 m/s) von der Drehachse eines mit ω = 0,5 s-1 links herum rotierenden Systems entfernt (siehe Abb. 1.11.14). Aus der Sicht des rotierenden Systems wird dieser Strahl mit der Winkelgeschwindigkeit ω nach rechts gedreht und bildet zum Zeitpunkt t den Winkel ω·t mit der x-Achse des zum rotierenden System gehörenden x-y-Koordinatensystems. In der Abb. 1.11.15 ist die mit dem Open-Office-Tabellenkalkulationsprogramm errechnete Bahn im rotierenden System dargestellt.
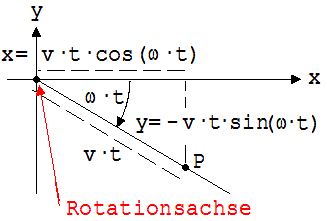
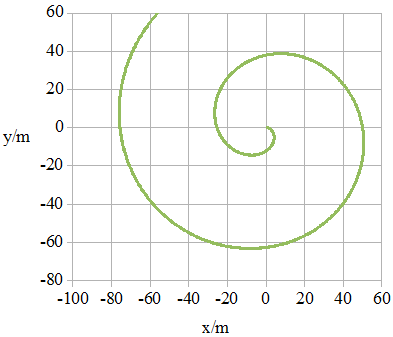
Abb. 1. 11.14 Abb. 1.11.15 Tabelle 16
Für einen Beobachter im rotierenden System entsteht diese Bahn unter der Wirkung der Zentrifugal- und der Corioliskraft.Er berechnet die Bahn mit Hilfe dieser Kräfte. Die Corioliskraft hat den Betrag 2·m·ω·v und die Koordinaten: C1 = 2 · m· ω· v2 ; C2 = - 2·m· ω· v1
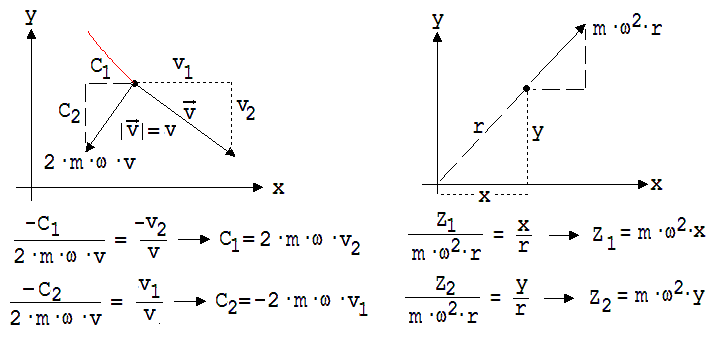
Abb. 1.11.16 Abb. 1. 11.17
Corioliskraft FC = {C1; C2 } = {2 · m· ω· v2 ; - 2·m· ω· v1} = 2·m· ω· {v2; -v1 }
Die Zentrifugalkraft hat den Betrag m·ω2·r und die Koordinaten Z1 = m·ω2·x und Z2 = m· ω2· y (siehe Abb. 1. 11.17).
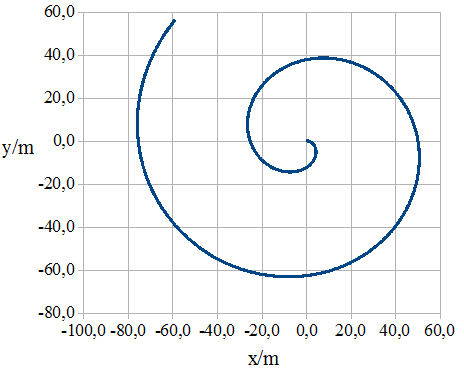
Abb. 1. 11.18 Tabelle 17
Die Coriolis- und die Zentrifugalkraft bilden zusammen die Kraftkoordinaten: F1 = 2·m·ω·v2 + m·ω2 · x und F2 = -2·m·ω·v1 + m·ω2 · y. Mit diesen Kräften erhält ein Beobachter im rotierenden System die in der Abb. 1.11.18 sichtbare Bahn. Sie gleicht der Bahn in der Abb. 1.11.15.
Erscheinungen auf der Erde, die als Zeichen der Corioliskraft gedeutet werden können
Es sind einige Erscheinungen auf der Erde zu nennen, die als Zeichen der Corioliskraft gedeutet werden können. So ist bekannt, dass bei den Flüssen Sibiriens das rechte Ufer steiler ist als das linke. Hierfür ist die Corioliskraft verantwortlich, welche den Wasserstrom nach rechts drückt. Die Erde dreht sich nach Osten, dies bedeutet, dass ein über dem Nordpol schwebender Beobachter die Erde in einer Linksdrehung sieht.

Abb. 1.11.19
Die Auswirkung der Corioliskraft sind bei genauer Betrachtung auch an mitteleuropäischen Flüssen wahrnehmbar. So sind zum Beispiel die flachen Uferzonen an der Donau östlich von Passau zwischen Obernzell und Schlögen auf der linken Seite des Flusses insgesamt erheblich länger als auf der rechten Seite (siehe Abb. 1.11.19). Auch Passatwinde sind Zeichen von Corioliskräften.
Am Äquator aufsteigende Luftmassen werden nach Westen gelenkt. Ebenfalls bekannt ist die Tatsache, dass abfließendes Badewasser das Abflussloch der Badewanne auf der Nordhalbkugel meistens mit einer Rechtsdrehung verlässt.
1.11.5 Das Foucaultpendel
Ein Fadenpendel schwinge über dem Nordpol. Aus der Sicht eines über dem Nordpol schwebenden Beobachters dreht sich die Erde links herum. Die Schwingungsebene des Pendels dreht sich dabei nicht mit. Für einen Beobachter auf der Erde dreht sich deshalb die Schwingungsebene des Pendels in 24 Stunden um 360° rechts herum. Er führt dies auf die am Pendelkörper angreifende Corioliskraft FC = 2 · m · ω · {vy ; -vx } mit ω = 2·π / 24h zurück.
Drehung des Foucaultpendels an einem Ort mit dem Breitengrad α < 90°
Ein Pendel schwinge an einem Ort mit dem Breitengrad α. Ihm sei ein Koordinatensytem zugeordnet, dessen y-Achse nach Norden und dessen x-Achse von Osten nach Westen weist. In der hier sichtbaren Abbildung zeigt die x-Achse in Blickrichtung.
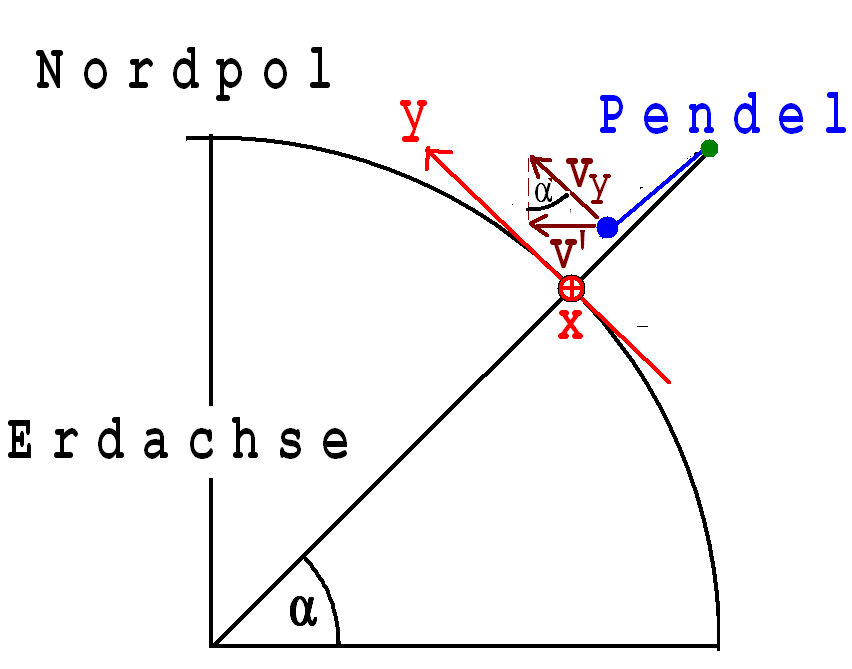
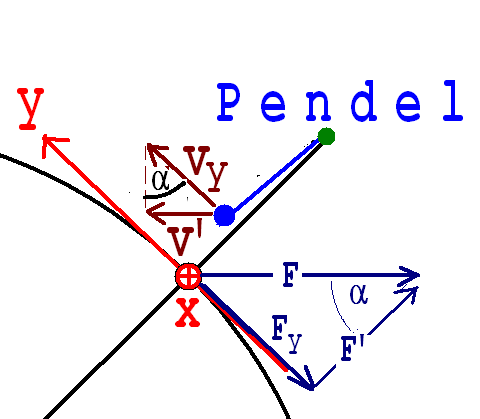
Abb. 1. 11.20 Abb. 1. 11.21
Für die x-Komponente der Corioliskraft ist die Geschwindigkeit v' (siehe Abb.1.11.20) maßgebend. Es ist die Komponente von vy parallel zur Äquatorebene.
v' = vy · sin α
Dementsprechend gilt für die x-Koordinate Fx der Corioliskraft:
Fx = 2 · m · v' · ω = 2 · m · vy· (sin α)· ω
Die Geschwindigkeit vx bewirkt im Fall vx > 0 eine von der Erdachse weg zeigende Kraft mit dem Betrag F = | 2 · m · vx · ω |. Diese Kraft kann als Summe der Kräfte F' und Fy aufgefasst werden (siehe Abb.1.11.21) Für die Drehung der Schwingungsebene ist F' ohne Bedeutung. Nur Fy in y-Richtung ist wichtig.
Fy = -F· (sin α) = - 2 · m · vx· (sin α)· ω
FD = {2 · m · vy· (sin α)· ω; - 2 · m · vx· (sin α)· ω} = 2 · m · sin (α)· ω ·{ vy ; - vx } ist die für die Drehung des Pendels maßgebende Kraft.
Am Nordpol ist sin (α ) = sin (90°) = 1. Dementsprechend wird dort ein Pendel unter der Kraft 2 · m · ω ·{ vy ; -vx } in 24h um 360° gedreht.
Ein Pendel an einem Ort mit 50° Breite verhält sich so wie auf dem Pol eines Planeten der sich mit der Winkelgeschwindigkeit (sin α)· ω dreht. Seine Pendelebene dreht sich deshalb nicht wie auf dem Pol der Erde um 360°, sondern um 360° ·sin(50°) = 275°.

Abb. 1.11.22: 1850 zeigt der französische Physiker Jean-Bernard-Leon Foucault durch einen Pendelversuch in der Pariser Sternwarte, dass sich die Erde dreht.