2.8 Transformationsgleichungen für eine Drehung

Mit der Programmzeile x=x+0,1; y=sin(x); u=x*cosg(a)-y*sing(a); v =x*sing(a)+y*cosg(a) in sim.html wird eine Sinuskurve gezeichnet und dann noch eine zweite Kurve, von der man annehmen kann, dass sie ursprünglich auf der ersten Kurve gelegen habe und dann von dieser um 120° weggedreht worden sei (siehe Abb.1).



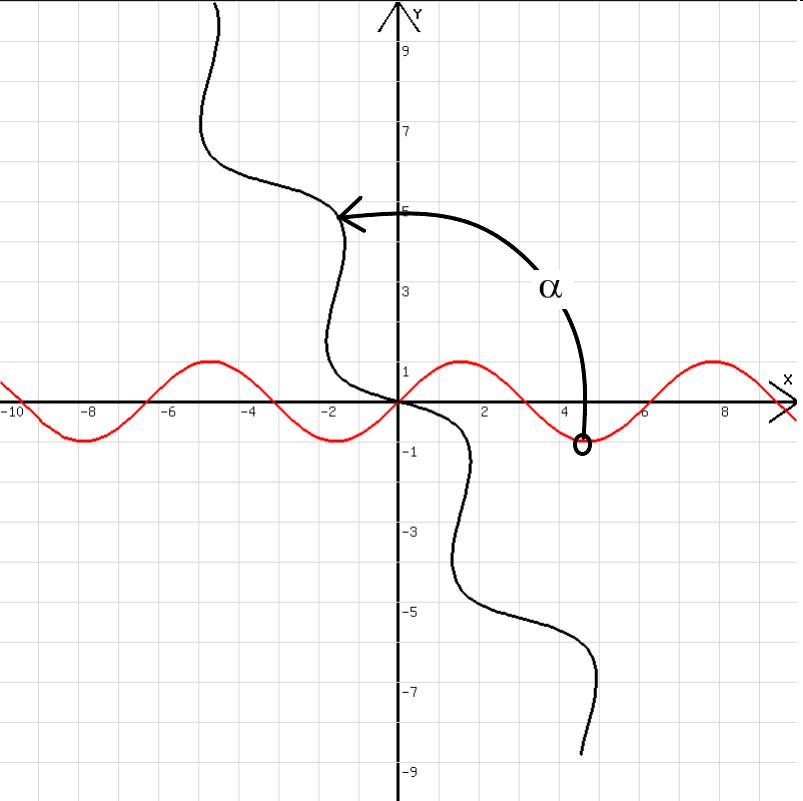
Abb.1

Wie führt ein Rechner dies Drehung aus ?

Mit  „x=x+0,1; y=sin(x);“ wird ein Punkt (x;y) gesetzt und mit „u=x*cosg(a)-y*sing(a); v =x*sing(a)+y*cosg(a)“ wird dem Punkt (x;y) einen Punkt (u;v) zugeordnet, der sich so verhält, als ob er vom Punkt P(x;y) um 120° um den 0-Punkt des Koordinatensystems weggedreht worden sei.

Herleitung der Zuordnungsvorschrift „u=x*cosg(a) -y*sing(a); v =x*sing(a)+y*cosg(a)“

Wie können die Koordinaten (u , v) eines um α gedrehten Punktes P mit  Hilfe   seiner   ursprünglichen Koordinaten (x; y)  berechnet werden ?

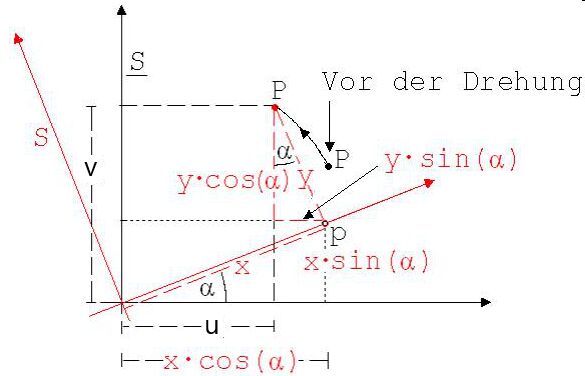
Abb. 2

Vor der Drehung gilt für P: u = x ; v = y.

P werde mit eine Kopie S des Achsensystems S um α (a) gedreht. Die x, y-Koordinaten  von P in S ändern sich dabei nicht. P wird nach der Drehung um einen Winkel α auf einen Punkt p der zu S gehörenden x-Achse projiziert. Für die Koordinaten dieses Punktes p gilt:

  u_p = x · cos(α);    v_p = x · sin(α)

Wie in der Abb.2 erkennbar, gilt für die Koordinaten u; v des gedrehten Punktes P: 

 u = x · cos α - y · sin α

v= x · sin α + y · cos α