1.1 Potenzen mit reellen Exponenten

Aufgabe:

Wir stellen  uns  vor, auf  einem Nährboden  für  Bakterien seien zu einem Zeitpunkt t = 0 etwa 100 Bakterien, die  sich  uneingeschränkt  vermehren können.  Es  soll untersucht werden, wie sich diese Bakterien mit zunehmender Zeit t vermehren. Bei dieser Untersuchung kann davon  ausgegangen werden, dass der Zuwachs Δb der  Bakterienzahl b in einem kleinen  Zeitabschnitt  Δt proportional zur augenblicklich  vorhandenen Zahl b der Bakterien  und zur Dauer Δt des Zeitabschnitts ist.

Δb  ~   b;  Δb  ~  Δt       →        Δb ~  b · Δt     →        Δb/(Δt ·b )  = Konstante = k        →    Δb   =  k · b · Δt

Somit gilt für die Bakterienzahl b' nach Δt:    b' = b + k ·b · Δt

Die Entwicklung der Bakterien bis zur Zahl b = 1000 wird mit dem folgenden Programm in sim.html beschrieben:

h=0,01; b = b + k*b*h; t = t + h; y=b; x=t; l=b

h=0,01 steht für Δt (Einheit: Stunde)

Im Variablenfeld von sim.html werden für b, k und n die Werte 100, 0,2 und 999 eingetragen.

Mit n = 999 wird der Abbruch des Programms mit b=l=1000 veranlasst.

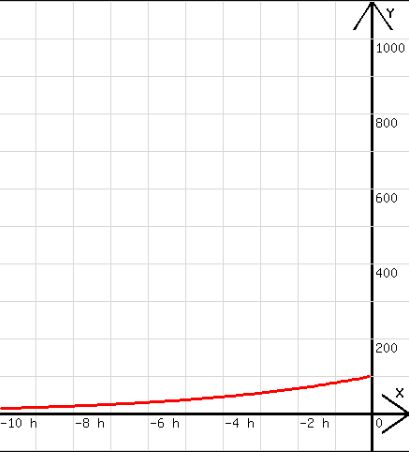
Nach „START“ entsteht das Diagramm in der Abb. 1.

Abb. 1                                                                                   Abb. 2

Das oben  angegebenen Programm beschreibt mit h = Δt < 0 auch die Entwicklung der Bakterien vor dem willkürlich gesetzten Zeitnullpunkt. So kann man erfahren, wie viele Bakterien zum Zeitpunkt – 1 Stunde ( eine Stunde vor dem Zeitnullpunkt) oder zum Zeitpunkt – 2 Stunden existiert haben. Wird z.B. für h der Wert -0,01 festgelegt, dann bestimmt das Programm im 1. Schritt die Zahl der Bakterien zum Zeitpunkt –h und im 2. Schritt die zum Zeitpunkt – 2·h usw..

Mit h = -0,01 wurde das nachfolgende Diagramm in Abb. 2 entwickelt.    In der Abb. 3 sehen wir beide Diagramme zusammen.

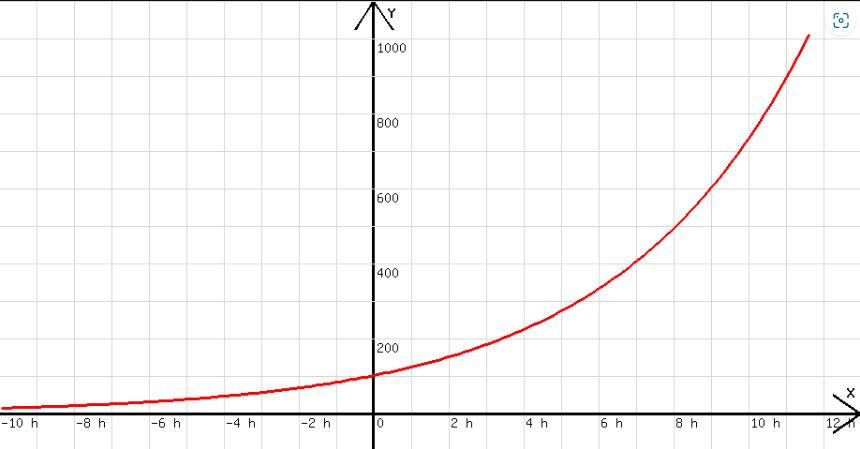
Abb. 3

An  dem  Diagramm  fällt auf ,  dass  3,46 Stunden nach jedem beliebigen  Zeitpunkt eine Verdopplung der Bakterienmenge stattfindet. Wenn  es  anfänglich  100  Bakterien  sind,  dann  existieren  nach  3,46 Stunden   200 Bakterien  und  nach weiteren 3,46 Stunden 400 Bakterien. Wenn  man  vom  Koordinatennullpunkt um 3,46  Stunden  nach  links  geht, dann findet  man  50 und nach weiteren 3,46 Stunden nur noch 25 Bakterien (siehe Abb. 4).

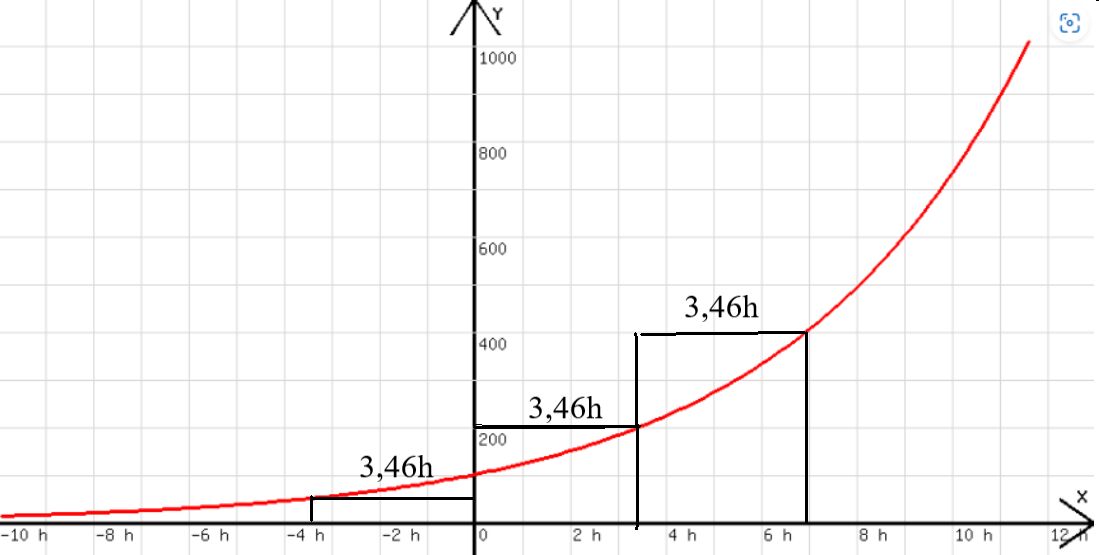
Abb. 4

In  der  folgenden  Tabelle  ist  dieser  Sachverhalt  übersichtlich  in  einer  Tabelle   zusammengefasst. T ist die Verdopplungszeit = 3,46 h.

Für Produkte wie 2·2·2 ,  2 ·2 und 2·2·2·2  ist die Schreibweisen  2³ bzw. 2² bzw. 2⁴ üblich.

Ein Term der Form a^c heißt Potenz von a, die Grundzahl b wird Basis  und die Hochzahl c wird Exponent genannt.

Angesichts des in der Tabelle erkennbaren  Sachverhalts ist man geneigt, das Bakterienwachstum durch b = 100 · 2^t/T darzustellen. Dies wird man jedoch zunächst nur dann zulassen, wenn die Exponenten natürliche Zahlen sind.

Zur Behebung dieser Einschränkung auf natürliche Zahlen soll nun eine Erweiterung des Potenzbegriffs versucht werden, so dass eine Beschreibung des Bakterienwachstums mit b = 100 · 2^t/T  auch dann als erlaubt gilt, wenn  t/T  keine natürliche Zahl ist.

1. Definition für ganzahlige negative Exponenten und den Exponent 0

Nach b = 100 · 2^t/T  erhalten wir für t = 0 den Wert  n = 100 · 2⁰.  Da anfangs 100 Bakterien vorhanden sind, muss 2⁰  als 1 definiert werden. Nach b = 100 · 2^t/T finden wir für die Zeiten –T und – 2· T  die Werte n = 100 · 2^-1 und   n = 100 · 2^-2. Diese Angaben können wir nur dann als sinnvoll anerkennen, wenn wir 2^-1 als 1/2 und 2^-2 als 1/ 2² definieren.

Wir vereinbaren deshalb: a⁰ = 1;    a^-n = 1/ aⁿ

2. Definition für Stammbrüche als Exponenten

Eine Definition  anhand  des Diagramms in  Abb. 3  scheint unmöglich. Vielleicht finden wir beim Umgang mit Potenzen Eigenschaften, die eine sinnvolle Definition ermöglichen. Beim Multiplizieren, Dividieren  und Potenzieren  von  Potenzen  mit   ganzzahligen  Exponenten  stößt man auf die folgenden Gesetzmäßigkeiten:

1. aⁿ · a^m = a ^{m + n} ;      Beispiel: a²· a³ = a · a · a · a · a = a⁵

2. aⁿ / a^m = a ^{n- m} ;       Beispiel: a⁴ / a⁶ = 1/a² = a ^–2  = a^{4 - 6}   

3. (aⁿ)^m = a^{n · m} ;         Beispiel:  (a³)² = (a · a · a) · (a · a · a) = a⁶ = a^{3 · 2}

4. (a · b)ⁿ = aⁿ · bⁿ

5. (a / b)ⁿ = aⁿ / bⁿ

Von Potenzen  mit  Bruchexponenten  fordern  wir, dass auch  sie die genannten Gesetzmäßigkeiten erfüllen. a^1/2 · a^1/2  sollte demnach gleich  a^1/2+1/2 = a¹ = a sein.   

a^1/2 · a^1/2  = a   →   

Wie soll a^1/3 definiert werden ?

Es soll gelten:  a^1/3 · a^1/3 · a^1/3  =  a^1/3+1/3+1/3  =  a.

a^1/3 ist demnach eine positive Zahl, die dreimal mit sich multipliziert a ergibt.

Wir schreiben für a^1/3 =  ( dritte Wurzel aus a).   

Beispiele: 

Wie soll a^1/4 definiert werden ?

Wir erwarten: a^1/4 · a^1/4 · a^1/4 ·  a^1/4 = a^{1/4+1/4+1/4+1/4} = a     →     a^1/4 =  ( vierte Wurzel aus a)

Beispiele: 

Wir definieren:   

Es besteht die Hoffnung, dass die so definierten Potenzen zur Beschreibung des Bakterienwachstums geeignet sind.  Nach der Gleichung n = 100 · 2^t/T gibt es zur Zeit t = T/2  n = 100 · 2^1/2    = 100 ·  ≈  141 Bakterien. Zu unserer Zufriedenheit kann dieser Wert am Diagramm in Abb. 5 (Ausschnitt aus dem Diagramm in Abb. 3)  abgelesen werden.

Abb. 5

3. Definition  einer Potenz mit einem beliebig  gewählten  Bruchexponenten

Wie soll a^2/3 definiert werden ?

Es soll gelten: a^1/3 · a^1/3 = a^2/3    →   

Wir definieren:

Es liegt nun nahe, die Gleichung b = 100·2^t/T erneut auf ihre Gültigkeit zu prüfen. Für t/T = 7/3 ( t = 7/3*3,46 h=8,07h) erhält man  nach der obigen Definition den Wert 504, eine Bakterienzahl, die zum Diagramm in der Abb. 3 passt. Da die Prüfung an einem einzigen Wert etwas unzureichend erscheint, soll nun noch der vom Wachstumsprogramm erzeugte Graph mit dem von w=100*2^(t/3.46) verglichen werden.

Dies geschieht mit der Programmzeile:

h=0,01;w=100*2^(t/3,46); t=t+h; k=0,2; b = b + k*b*h; y=b; x=t; l=b (Anfangswerte: t = -10h; b = 100*2^(-10/3,46) =13,5)

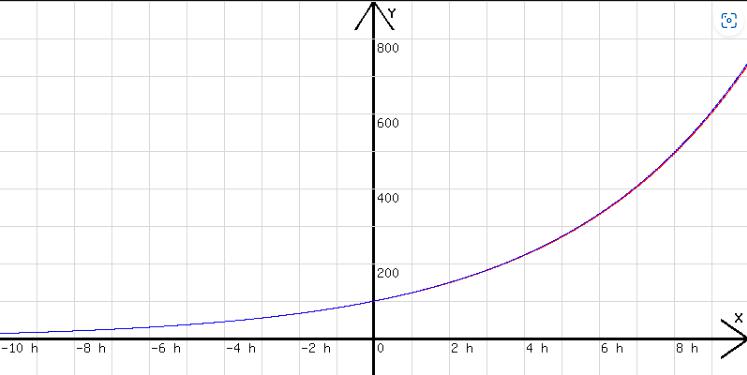
Abb. 6

Die rote Programmkurve wird von einer blauen Kurve zu w = 100 * 2^(t/3,46)  überdeckt.

Es muss noch angemerkt werden, dass die Potenzgesetze nach der Definition für Bruchexponenten ihre Gültigkeit uneingeschränkt behalten. Außerdem muss darauf aufmerksam gemacht werden, dass eine Potenz ihren Wert nicht ändert, wenn der Bruchexponent erweitert bzw. gekürzt wird.

Die letzte Angabe ist keineswegs selbstverständlich, sie muss bewiesen werden.

Beweis: 

Es wird erst die linke und dann die rechte  Seite der letzten Gleichung  mit   k · n   potenziert. Wenn die Behauptung richtig ist, dann müssen beide Ergebnisse übereinstimmen. Nach dem 3. Potenzgesetz gilt:

 ↓

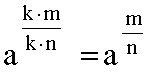
4. Definition für irrationale Exponenten

An einem Beispiel wird gezeigt, wie bei irrationalen Exponenten vorzugehen ist. Wir wissen, dass die irrationale Zahl durch die folgende Intervallschachtelung erfasst wird:

Dieser Intervallschachtelung können wir die nun folgende Intervallschachtelung zuordnen:

Wir stellen uns die Intervallschachtelung auf einer Zahlengeraden vor. Sie erfasst einen Einschnitt auf der Zahlengeraden, den wir als  bezeichnen.

Es  ist noch  darauf  hinzuweisen, dass  die  Definition einer Potenz mit Bruchexponent auf positive Grundzahlen  beschränkt werden muss.  Diese  Einschränkung  wird verständlich, wenn man bedenkt, dass Wurzeln der Form  (n = gerade) nicht aus negativen Zahlen gezogen werden können, so ist z.B. in der Menge der reellen Zahlen die Quadratwurzel aus – 2  nicht definiert.